Shortest-path algorithms with external memory

A shortest path algorithm 's Algorithmic an algorithm set within a graph , the shortest path between two or more nodes is. In many cases, the input data for the algorithm is too large for the main memory , so that a large part of the data is located on external storage (e.g. a hard disk or tape drive ).

Since access to this external memory is much slower, specially adapted external memory or out-of-core algorithms are used as a rule . With this type of algorithm, you usually want to minimize the number of (slow) accesses to the external memory.

General

There are different variants of the shortest path problem with regard to the start and destination nodes. In the following, algorithms are presented that calculate the shortest paths to all other nodes from a single starting node. This problem is also known as the Single-Source Shortest Path (SSSP).

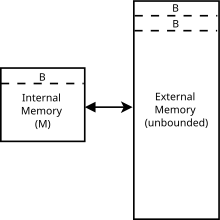
Representation of the external memory model

The external memory model is often used to model the memory model. The system has a main memory with a limited size but very fast access times. In addition, there is an external memory of any size that can be accessed slowly and in blocks of the same size . ${\ textstyle M}$ ${\ textstyle B}$

Adaptation of the Dijkstra algorithm

The Dijkstra algorithm offers a possible solution to the SSSP problem . The idea of this greedy algorithm is to always follow the edges, starting from the starting node, which lead to the next not yet reached node with the shortest path. To do this, the next possible nodes are stored in a priority queue .

The Dijkstra algorithm can be converted into an external algorithm by replacing the priority queue used with appropriately adapted external memory data structures. However, one encounters the following problems:

In every step of the algorithm there is access to all adjacent (connected) edges of a node. In the worst case, an IO operation must be performed on the external memory in every step. As a result, the runtime is very bad, especially with sparsely populated graphs. So far there is no known algorithm that solves the problem on any graph. However, there are solutions for special graphs, such as B. planar graphs .
The algorithm always saves which nodes have already been reached. This problem can be solved by running the algorithm in phases. In each phase, the nodes that have already been visited are stored in a hash table . The size of the hash table is limited so that it fits in the main memory. As soon as the hash table is full, the next phase begins. In this, the complete graph is first run through and all edges that lead to nodes that have already been visited are removed. The hash table is then emptied and the actual Dijkstra algorithm continues.
The priority queue used must support a decrese_key operation, i.e. a function with which the priority of an element in the queue can be reduced later. This is necessary because shorter paths to a node that is already in the queue can be discovered during the algorithm. Many well-known external memory priority queues only offer this function with additional IO operations.

However, if a phased algorithm is used, as mentioned above, a node can be added to the queue multiple times. In this case, nodes must be ignored that have already been visited because they have been added to the queue several times. When changing to the next phase, you can scan the queue in this variant and remove all nodes that have already been visited.

Overall, for the phased algorithm, this means that access to the external memory is required. It specifies the number of nodes, the number of edges and the size of the main memory. It also specifies the number of IO operations required when running through values and the number of IO operations when sorting values. ${\ displaystyle {\ mathcal {O}} \ left (| V | + \ left \ lceil {\ frac {| V |} {M}} \ right \ rceil \ cdot \ operatorname {scan} (| V | + | E |) + \ operatorname {sort} (| E |) \ right)}$ ${\ displaystyle | V |}$ ${\ displaystyle | E |}$ ${\ displaystyle M}$ ${\ displaystyle \ operatorname {scan} (n)}$ ${\ displaystyle n}$ ${\ displaystyle \ operatorname {sort} (n)}$ ${\ displaystyle n}$

Implementation with Tournament Trees

Instead of a priority queue, you can also use other data structures, such as the so-called tournament trees. In this case, the elements in the queue are represented as a binary tree . The idea is that the elements are arranged like a tournament with a knockout system . In each node (except for the leaves ) are the elements from the child nodes that have the highest priority. The principle can be clearly seen in the example on the right. Here the elements in the tree with a smaller number have a higher priority. As a result, the two smallest elements are located in the root of the tree. A tournament tree is a complete tree with the exception that leaves may be missing at the lowest depth from the right.

Exemplary structure of a tournament tree with two values per node (without signals)

In our case, the tournament tree contains elements consisting of a tuple with a node and a key according to which the elements are sorted. The Tournament Tree offers the following features: ${\ textstyle x}$ ${\ textstyle k}$

deletemin : Outputs the element with the smallest key and replaces it with . ${\ displaystyle (x, k)}$ ${\ displaystyle (x, \ infty)}$

delete (x) : Replaces the element with .

{\ displaystyle (x, oldkey)}

{\ displaystyle (x, \ infty)}

update (x, newkey) : Replaces the element with if

{\ displaystyle (x, oldkey)}

{\ displaystyle (x, newkey)}

{\ displaystyle newkey <oldkey}

This data structure can be implemented efficiently with external storage. For this, the individual operations are not immediately applied to all nodes in the tree, but are saved as so-called signals in the individual nodes. Each node consists of two buffers in which the elements of the node or the signals are stored. Up to objects can be saved in each buffer . The size must be selected so that a node fits completely into the main memory. ${\ displaystyle M}$ ${\ displaystyle M}$

At the beginning all nodes of the tree are initialized as keys. The signal buffers are initially empty. In principle, signals are always inserted at the root. There are two different types of signals: ${\ textstyle \ infty}$

Delete signals are always forwarded to the corresponding child nodes up to the leaves. This signal removes the element from the buffer for all nodes. The leaves are an exception: Here the key of the element is set to. ${\ textstyle \ infty}$
Update signals are forwarded to the child nodes until the current node contains the element to be changed. If the current key of the element in the node is smaller than the new key contained in the update signal, the signal is discarded. Otherwise the key will be changed and the signal forwarded.

When a signal is added to a node, the changes are first made to the node itself. If the signal has to be forwarded, it is inserted into the signal buffer. As soon as the buffer is full, it must be emptied. This is done by forwarding the signals to the appropriate child nodes. It should be noted that when the signals are passed on to the child nodes, the node must first be loaded into the main memory.

If a node has fewer than elements in the buffer, the node must be filled. To do this, the signal buffer must first be emptied as described above. The node is then filled with the elements of the highest priority. If a child node has fewer than elements due to the emptying of the signal buffer, the child node must first be filled recursively. ${\ textstyle {\ frac {M} {2}}}$ ${\ textstyle M}$ ${\ textstyle {\ frac {M} {2}}}$

The maximum number of accesses to the external memory required for a sequence of operations is: ${\ textstyle k}$

${\ displaystyle {\ mathcal {O}} ({\ frac {k} {B}} log_ {2} {\ frac {N} {B}})}$

Dijkstra can be modified with this data structure in order to efficiently solve the SSSP problem in the external memory model. The priority queue is replaced by the tournament tree. The total number of IO operations that the algorithm requires is:

${\ displaystyle {\ mathcal {O}} \ left (| V | + {\ frac {| E |} {B}} log_ {2} {\ frac {| E |} {B}} \ right)}$

where is the block size that is transferred during an IO operation. ${\ textstyle B}$

Individual evidence

^ Peter Sanders: Memory Hierarchies - Models and Lower Bounds . In: Algorithms for Memory Hierarchies: Advanced Lectures (= Lecture Notes in Computer Science ). Springer Berlin Heidelberg, Berlin, Heidelberg 2003, ISBN 978-3-540-36574-7 , pp. 5-7 , doi : 10.1007 / 3-540-36574-5_1 .
↑ ^a ^b Irit Katriel, Ulrich Meyer: Elementary Graph Algorithms in External Memory . In: Algorithms for Memory Hierarchies: Advanced Lectures (= Lecture Notes in Computer Science ). Springer Berlin Heidelberg, Berlin, Heidelberg 2003, ISBN 978-3-540-36574-7 , pp. 62-84 , doi : 10.1007 / 3-540-36574-5_4 .
↑ Lars Arge, Gerth Stolting Brodal, Laura Toma: On external-memory MST, SSSP and multi-way planar graph separation . In: Journal of Algorithms . tape 53 , no. 2 , November 1, 2004, ISSN 0196-6774 , p. 186–206 , doi : 10.1016 / j.jalgor.2004.04.001 ( sciencedirect.com [accessed July 30, 2019]).
↑ ^a ^b Yi-Jen Chiang, Michael T. Goodrich, Edward F. Grove, Roberto Tamassia, Darren Erik Vengroff: External-memory Graph Algorithms . In: Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms (= SODA '95 ). Society for Industrial and Applied Mathematics, Philadelphia, PA, USA 1995, ISBN 978-0-89871-349-7 , pp. 139–149 ( acm.org [accessed July 30, 2019]).
^ Vijay Kumar, Eric J. Schwabe: Improved Algorithms and Data Structures for Solving Graph Problems in External Memory . In: Proceedings of the 8th IEEE Symposium on Parallel and Distributed Processing (SPDP '96) (= SPDP '96 ). IEEE Computer Society, Washington, DC, USA 1996, ISBN 978-0-8186-7683-3 , pp. 169– ( acm.org [accessed July 30, 2019]).

[1] Peter Sanders: Memory Hierarchies - Models and Lower Bounds . In: Algorithms for Memory Hierarchies: Advanced Lectures (= Lecture Notes in Computer Science ). Springer Berlin Heidelberg, Berlin, Heidelberg 2003, ISBN 978-3-540-36574-7 , pp. 5-7 , doi : 10.1007 / 3-540-36574-5_1 .

[:0-2] Irit Katriel, Ulrich Meyer: Elementary Graph Algorithms in External Memory . In: Algorithms for Memory Hierarchies: Advanced Lectures (= Lecture Notes in Computer Science ). Springer Berlin Heidelberg, Berlin, Heidelberg 2003, ISBN 978-3-540-36574-7 , pp. 62-84 , doi : 10.1007 / 3-540-36574-5_4 .

[3] Lars Arge, Gerth Stolting Brodal, Laura Toma: On external-memory MST, SSSP and multi-way planar graph separation . In: Journal of Algorithms . tape 53 , no. 2 , November 1, 2004, ISSN 0196-6774 , p. 186–206 , doi : 10.1016 / j.jalgor.2004.04.001 ( sciencedirect.com [accessed July 30, 2019]).

[:1-4] Yi-Jen Chiang, Michael T. Goodrich, Edward F. Grove, Roberto Tamassia, Darren Erik Vengroff: External-memory Graph Algorithms . In: Proceedings of the Sixth Annual ACM-SIAM Symposium on Discrete Algorithms (= SODA '95 ). Society for Industrial and Applied Mathematics, Philadelphia, PA, USA 1995, ISBN 978-0-89871-349-7 , pp. 139–149 ( acm.org [accessed July 30, 2019]).

[5] Vijay Kumar, Eric J. Schwabe: Improved Algorithms and Data Structures for Solving Graph Problems in External Memory . In: Proceedings of the 8th IEEE Symposium on Parallel and Distributed Processing (SPDP '96) (= SPDP '96 ). IEEE Computer Society, Washington, DC, USA 1996, ISBN 978-0-8186-7683-3 , pp. 169– ( acm.org [accessed July 30, 2019]).