Conical combination

A conical combination (sometimes non-negative combination or conical linear combination ) and the closely related positive combination , specific linear combinations in which all coefficients are non-negative and positive, respectively. They mostly occur in connection with convex cones .

definition

Given a vector space and . Then a conical combination or nonnegative combination of , if there is in , is called such that ${\displaystyle \mathbb {R} }$ ${\displaystyle V}$ ${\displaystyle x,x_{1},\dots ,x_{n}\in V}$ ${\displaystyle x}$ ${\displaystyle x_{1},\dots ,x_{n}}$ ${\displaystyle \lambda _{1},\dots ,\lambda _{n}\geq 0}$ ${\displaystyle \mathbb {R} }$

${\displaystyle x=\sum _{i=1}\lambda _{i}x_{i}}$

applies. If all are , then one speaks of a positive combination. ${\displaystyle \lambda _{i}>0}$

A linear combination with non-negative (or positive) coefficients is called a non-negative (or positive) combination.

properties

The (infinitely extended) conical hull of two vectors im ${\displaystyle \mathbb {R} ^{2}}$

• More generally, the above terms can also be defined for any vector spaces as long as there is an ordered body . ${\displaystyle \mathbb {K} }$ ${\displaystyle \mathbb {K} }$
• Every convex combination is a conical combination.
• The shell belonging to the conical combination is called the conical shell or positive shell and is designated with the symbol (sometimes ambiguously also with ). It assigns to each subset of a vector space the smallest convex cone that contains this subset ${\displaystyle \operatorname {pos} (A)}$ ${\displaystyle \operatorname {cone} (A)}$

example

The polynomial is a conical combination of the monomials with . Thus it is also a positive combination of the monomials. If, on the other hand, one chooses as monomials , it is only a conical combination and not a positive combination, there is. ${\displaystyle 3x^{2}+5x+2}$ ${\displaystyle x^{2},x,1}$ ${\displaystyle \lambda _{2}=3,\,\lambda _{1}=5,\lambda _{0}=2}$ ${\displaystyle x^{3},x^{2},x,1}$ ${\displaystyle \lambda _{3}=0,\lambda _{2}=3,\,\lambda _{1}=5,\lambda _{0}=2}$

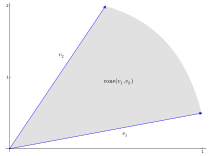
Looking at the vectors ${\displaystyle \mathbb {R} ^{2}}$

${\displaystyle v={\begin{pmatrix}2\\2\end{pmatrix}},\,v_{1}={\begin{pmatrix}1\\0\end{pmatrix}},\,v_{2}={\begin{pmatrix}1\\1\end{pmatrix}},\,v_{3}={\begin{pmatrix}1\\2\end{pmatrix}}}$,

so can be represented in more than one way as a conical combination of . Since and are linearly dependent , is a possible conical combination . A second possibility would be a combination . Both are not positive combinations, since one of the coefficients is always zero. ${\displaystyle v}$ ${\displaystyle v_{1},v_{2},v_{3}}$ ${\displaystyle v}$ ${\displaystyle v_{2}}$ ${\displaystyle v=0v_{1}+2v_{2}+0v_{3}}$ ${\displaystyle v=1v_{1}+0v_{2}+1v_{3}}$

literature

• Peter Knabner , Wolf Barth : Lineare Algebra. Basics and applications (=  Springer textbook ). Springer Spectrum, Berlin et al. 2013, ISBN 978-3-642-32185-6 .
• Stephen Boyd, Lieven Vandenberghe: Convex Optimization. Cambridge University Press, 2004, ISBN 978-0-521-83378-3 ( online ).