Locally contiguous
Locally connected spaces are considered in the mathematical sub-area of topology . These are topological spaces that are connected around each point in a small way.
Definitions
- A topological space is said to be locally connected at the point if it has a neighborhood basis of open and connected sets.
- A topological space is said to be locally connected if it is locally connected in each of its points.
By including the definition of the environment base in the above definition, this can also be reformulated as follows:
- A topological space is locally connected if for each and every open set with an open and connected set are with .
Examples
- Every open set is locally connected with its subspace topology , because for each the spheres located completely in form a surrounding base of the required kind.
- The union of two or more disjoint, non-empty sets im shows that locally connected spaces are in general not connected.
- The unit interval , the unit square , the general cuboid im are locally connected.
- Discrete spaces and spaces with the trivial topology are locally connected. In the first case, each one-point set is an environment basis of the contained point, in the second case the total space is an environment basis.
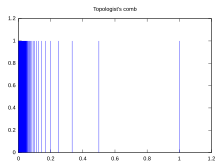
- The topological ridge is not locally connected in the points , since sufficiently small spheres around these points always consist of an infinite number of disconnected lines. Since this space is connected, this example shows that connected spaces are generally not locally connected.
- The space with the subspace topology of is not locally connected at any point.
- Every topological space has a coarsest locally connected topology that is finer than , namely
- It is clear that the discrete topology is always included in the set over which the average is formed. One then shows that this intersection is a locally connected topology .
- The transition from a topological space to the locally connected space constructed in this way is a functor that is right adjoint to the forgetting functor that forgets the local context. The category of locally connected spaces is accordingly a core-reflective sub-category in the category of topological spaces.
Equivalent characterizations
- A topological space is locally connected if and only if every connected component of every open set is open.
- A topological space is locally connected if and only if the open and connected sets form a basis of the topology.
properties
- Open subspaces of locally connected spaces are again locally connected, as can be seen directly from the definition. Arbitrary subspaces are generally not locally connected again. The above example of the topological ridge is a closed subspace of the locally connected unit square .
- Quotient spaces of locally connected spaces are again locally connected.
- In general, continuous images of locally connected spaces are not locally connected again. But the following applies:
- If there is a continuous, surjective mapping of a compact, locally connected space onto a Hausdorff space , then is locally connected.
- Finite products of locally connected spaces are again locally connected. This is generally wrong for any product. The following applies here:
- If a family of locally connected spaces is then the product is locally connected if and only if all exceptions are connected up to a finite number.
- The category of locally connected rooms is a category with any products. The product of a family in the category of locally connected spaces is the Cartesian product provided with the coarsest locally connected topology, which is finer than the product topology .
Hahn-Mazurkiewicz's theorem
Hahn-Mazurkiewicz's theorem, named after Hans Hahn and Stefan Mazurkiewicz , characterizes those Hausdorff spaces that are quotient spaces of the unit interval. According to the above, these must be locally connected, but properties such as compactness , connection and the second axiom of countability follow immediately. The reverse is the nontrivial direction in the following theorem
- Hahn-Mazurkiewicz theorem : A Hausdorff space is exactly the quotient space of the unit interval if it is compact, connected, locally connected and has a countable basis.
Contiguous, compact Hausdorff spaces with a countable base are also called continua . With this, Hahn-Mazurkiewicz's theorem can be reformulated as follows:
- A continuum is a quotient space of the unit interval if and only if it is locally connected.
In particular, is a compact and connected subset of the continuous image of the unit interval if and only if it is locally connected.
Individual evidence
- ↑ Michael Starbird, Francis Su: Topology Through Inquiry , Ams / Maa Textbooks 2019, Volume 58, ISBN 978-1-470-45276-6 , chap. 8.5: Local connectedness
- ↑ Stephen Willard: General Topology , Dover Publications 1970, ISBN 0-48643479-6 , definition 27.7
- ↑ B. v. Querenburg: Set theoretical topology , Springer-Verlag 2001, ISBN 978-3-540-67790-1 , definition 4.16 (b)
- ^ HJ Kowalsky: Topological Spaces , Springer-Verlag 1961, chap. III, §15.3: Local context
- ↑ Stephen Willard: General Topoloy , Dover Publications 1970, ISBN 0-48643479-6 , Theorem 9/27
- ↑ Michael Starbird, Francis Su: Topology Through Inquiry , Ams / Maa Textbooks 2019, Volume 58, ISBN 978-1-470-45276-6 , Theorem 8.24
- ↑ Stephen Willard: General Topoloy , Dover Publications 1970, ISBN 0-48643479-6 , Theorem 12/27
- ^ LA Steen, JA Seebach: Counterexamples in Topology , Dover Publications 1978, ISBN 978-0-486-68735-3 , Section 4: Connectedness , page 31
- ↑ Lynn A. Steen, J. Arthur Seebach, Jr.,: Counterexamples in Topology. 1970 Section 4; Connectedness , p. 31
- ^ N. Bourbaki, General Topology, Chapters 1-4, Springer Verlag 1989, ISBN 3-540-64241-2 , §11.6: Locally connected spaces , sentence 13
- ↑ B. v. Querenburg: Set theoretical topology , Springer-Verlag 2001, ISBN 978-3-540-67790-1 , sentence 4.17 (d)
- ↑ H. Herrlich, GE Strecker: Category Theory , Ally and Bacon Inc. 1973, Example 18.8 (5)
- ↑ Katsuro Sakai: Geometric Aspects of General Topology , Springer-Verlag 2013, ISBN 978-4-431-54397-8 , chap. 5.14: Appendix: The Hahn-Mazurkiewicz Theorem










![{\ displaystyle K = (\ {{\ tfrac {1} {n}} | n \ in \ mathbb {N} \} \ times [0,1]) \ cup ([0,1] \ times \ {0 \}) \ cup (\ {0 \} \ times [0,1]) \ subseteq \ mathbb {R} ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4be4b1ced730c19021953157e034b372b85014a9)
![{\ displaystyle \ {0 \} \ times (0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01c9697d05fbb7c7c383fea878ae14a4c7849e77)






![{\ displaystyle [0,1] \ times [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92f35a051af39d8299688d7c4a63e39ee5f95c8b)




