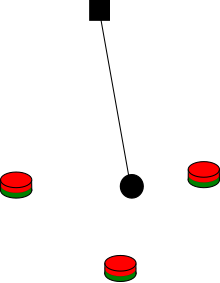
Magnetic pendulum

Sketch of a magnetic pendulum. A thread pendulum with an iron ball swings over three magnets. Depending on the starting position and speed, the pendulum will stop over a magnet in its final state.

Classification of the behavior of a magnetic pendulum over three magnets. Each point corresponds to a starting point for the pendulum movement. The color characterizes the magnet on which the pendulum comes to a standstill. The lighter the color, the sooner it will be. The three brightest points therefore mark the positions of the magnets.

A magnetic pendulum (also: chaos pendulum ) consists of an iron ball suspended on a thread, which hangs over a number of magnets attached to the floor . The length of the thread is chosen so that the ball just can't touch the magnets. If you deflect the pendulum , the ball, under the influence of gravity and magnetic attraction, executes oscillatory movements over the magnet. If the deflection and thus the energy is large enough that the pendulum can repeatedly detach itself from the attraction of the individual magnets, the result is an irregular movement curve that is sensitive to the starting position of the pendulum. The final state (magnet 1 = red, magnet 2 = green, magnet 3 = blue) is deterministic , that is, the movement of the pendulum is unambiguous given the initial conditions, but since it depends sensitively on the initial conditions, it is the movement of the pendulum around deterministic chaos .

Magnetic pendulum with a friction constant that decreases over time

Color chart

The real magnetic pendulum or the theoretical model with considered friction forces comes to a standstill at one of the magnets. The smallest changes in the starting position lead the pendulum to different magnets. This is especially evident when looking at a map where each possible starting point is marked with a color that characterizes the magnet that will eventually capture the pendulum. The lower the friction, the more delicate the areas of a certain color become in certain areas. See Figure 2. The adjacent video shows that the area with chaotic initial conditions (ie initial conditions that lead to an unpredictable end state with the smallest change) becomes larger the lower the friction in the pendulum system.

Mathematical model

The following forces act on the iron ball:

• Gravitation : with . ${\displaystyle {\vec {F}}_{g}=\nabla (m\,{\vec {g}}\cdot {\vec {r}})}$ ${\displaystyle {\vec {g}}=(0,0,-g)}$
• Attractions of the three magnets: . ${\displaystyle {\vec {F}}_{m}=-\nabla \sum _{i=0}^{N=3}V_{i}({\vec {r}})}$
• Frictional forces: air friction and bearing friction . ${\displaystyle {\vec {F}}_{r}=-\gamma \,{\dot {\vec {r}}}}$

Here is the mass of the iron ball, the acceleration due to gravity and the position of the iron ball. The magnetic force must be calculated from the potentials of the individual magnets. One can assume as potential, with the position of the -th magnet and its strength and potency . The friction is assumed here as Stokes friction with a coefficient of friction . From these assumptions, a differential equation can be set up that describes the movement of the pendulum: ${\displaystyle m}$ ${\displaystyle g}$ ${\displaystyle {\vec {r}}}$ ${\displaystyle V_{i}}$ ${\displaystyle V_{i}={\frac {\alpha _{i}}{|{\vec {r}}-{\vec {r}}_{i}|^{b}}}}$ ${\displaystyle {\vec {r}}_{i}}$ ${\displaystyle i}$ ${\displaystyle \alpha _{i}}$ ${\displaystyle b}$ ${\displaystyle \gamma }$

${\displaystyle m\,{\ddot {\vec {r}}}=\nabla (m\,{\vec {g}}\cdot {\vec {r}})-\nabla \sum _{i=0}^{N=3}V_{i}({\vec {r}})-\gamma \,{\dot {\vec {r}}}}$.

It is a system of three nonlinear differential equations of the second order. A solution to the initial condition can now be determined using numerical integration , for example . ${\displaystyle {\vec {r}}(t)}$ ${\displaystyle ({\vec {r}}(0),{\dot {\vec {r}}}(0))}$

Web links

• Program to simulate a magnetic pendulum and details about the simulation
• Java program to simulate a magnetic pendulum of the chair for physics and its didactics at the University of Würzburg
• Dominik Leiner: The Magnetic Pendulum - An Example of Deterministic Chaos (PDF file; 1.83 MB)
• Magnetic Pendulum (English)