Merge algorithms

Merge algorithms (of English merge , 'merge) are a family of algorithms, a plurality of sorted lists as input and output received a single ordered list, which contains all the elements of the input lists. Merge algorithms are used as a subroutine in many algorithms . A well-known example of this is mergesort .

application

Example of mergesort

The merge algorithm plays an important role in the mergesort algorithm, a comparison-based sorting algorithm . Conceptually, the mergesort algorithm consists of two steps:

Divide the input recursively into shorter lists of roughly the same length until each list contains only one element. A list that contains only one element is sorted by definition.
Repeatedly merge the shorter lists until a single list contains all of the items. This list is now the fully sorted list.

The merge algorithm is executed over and over as part of the mergesort algorithm.

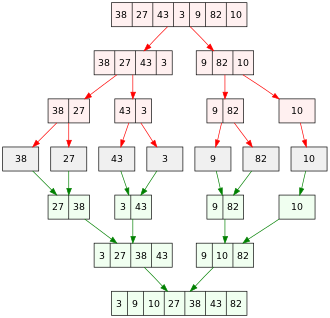
An example of mergesort is shown in the picture. You start with an unsorted list of 7 numbers. The array is divided into 7 partitions, each of which contains only one element. The sorted lists are then merged to provide longer sorted lists until there is only one sorted list left.

Merging two lists

The merging of two sorted lists can be done in linear time complexity and with linear space. The following pseudocode shows an algorithm which merges two lists Aand Binto a new list C. The function kopfreturns the first element in the list. Removing the first element is typically implemented by incrementing a pointer.

programm merge(A, B)
    eingabe A, B : Liste
    ausgabe Liste

    C := neue leere Liste
    solange A ist nicht leer und B ist nicht leer
        wenn kopf(A) ≤ kopf(B) dann
            hänge kopf(A) an C an
            entferne den Kopf von A
        sonst
            hänge kopf(B) an C an
            entferne den Kopf von B

    // Entweder A oder B ist leer. Nun muss noch die andere Liste an C angehängt werden.
    solange A ist noch nicht leer
        hänge kopf(A) an C an
        entferne den Kopf von A
    solange B ist noch nicht leer
        hänge kopf(B) an C an
        entferne den Kopf von B

    ausgabe C

Creating a new list Ccan be avoided. However, this makes the algorithm slower and harder to understand.

k -way mixing

With k -way shuffling, k sorted lists are merged into a single, sorted list that contains the same elements as the original lists. Let n be the total number of elements. Then n is the size of the output list and also the sum of the sizes of the input lists. The problem can be solved in a running time of O (n log k) and with a space requirement of O (n). Different algorithms exist.

Direct k -way mixing

The idea of direct k -way shuffling is to find the smallest element of all k lists and append it to the output. A naive implementation would be to search through all k lists at each step to find the minimum. This solution has a running time of Θ (kn). This works in principle, but is not particularly efficient.

The running time can be improved by the fact that the smallest element can be found faster. By using heaps or tournament trees, the smallest element can be found in time O (log k). The resulting time for the merging is then a total of O (n log k).

Heaps are often used in practice, but tournament trees have a slightly better running time. A heap needs about 2 * log (k) comparisons in each step, as it works the tree from the root down to the leaves. A tournament tree, on the other hand, only needs log (k) comparisons, since it starts at the bottom of the tree and works its way up to the root with only one comparison per level. For this reason, tournament trees should be used in preference.

Heap

The heap algorithm creates a min heap with pointers to the input lists. The pointers are sorted according to the element they are pointing to. The heap is created by an heapifyalgorithm in a runtime of O (k). The algorithm then iteratively stores the element pointed to by the root pointer in the output and executes an increaseKeyalgorithm on the heap. The running time for the increaseKeyalgorithm is O (log k). Since n elements have to be merged, the total running time is O (n log k).

Tournament tree

The tournament tree is based on a tournament in the knockout system , as used in sports. In every game, two of the input elements compete against each other. The winner will be passed up. For this reason, a binary tree is formed from games. The list is sorted here in ascending order, so the winner of a game is always the smaller of the elements.

Loser tree

With k -way shuffling, it is more efficient to save only the loser of each game (see graphic). The resulting data structure is loser tree ( Loser tree called). When building the tree or when replacing an element, the winner is still passed on to the top. The tree is filled like in a normal sports tournament, but only the loser is saved in each node. Usually an additional node is inserted above the root, which saves the entire winner. Each sheet stores a pointer to one of the input lists. Each inner node stores a value and a pointer to one of the input lists. The value contains a copy of the first element of the associated list.

The algorithm iteratively appends the smallest element to the return list and then removes the element from the associated input list. It then updates all nodes on the way from the updated leaf to the root ( replacement selection ). The item previously removed is the overall winner. The winner has won every game on the path between the input list and the root. If a new element is now selected, it must compete against the losers of the last round. By using a loser tree, the respective opponents are already stored in the nodes. The loser of each new game played is written into the node and the winner is given further up towards the root. When the root is reached, the overall winner is found and a new round of merging can begin.

The tournament tree and loser tree images in this section use the same data and can be compared for a better understanding.

algorithm

A tournament tree can be represented as a perfect binary tree by adding sentinels to each list and expanding the number of input lists to a power of two with empty lists. Then it can be represented in a single array. The parent element is reached by dividing the current index by 2.

If one of the hands is updated, all games are played again from this hand upwards. In the following pseudocode , no array is used for easier understanding, but an object-oriented approach. In addition, it is assumed that the number of sequences entered is a power of two.

programm merge(L1, …, Ln)
  erstelleBaum(kopf von L1, …, Ln)
  solange Baum hat Elemente
    gewinner := baum.gewinner
    ausgabe gewinner.wert
    neu := gewinner.zeiger.nächsterEintrag
    spieleNeu(gewinner, neu) // Replacement selection

programm spieleNeu(knoten, neu)
  verlierer, gewinner := spiele(knoten, neu)
  knoten.wert := verlierer.wert
  knoten.zeiger := verlierer.zeiger
  wenn knoten nicht Wurzel
    spieleNeu(knoten.parent, gewinner)

programm erstelleBaum(elemente)
  nächsteEbene := new Array()
  solange elemente nicht leer
    el1 := elemente.take() // ein Element nehmen
    el2 := elemente.take()
    verlierer, gewinner := spiele(el1, el2)
    parent := new Node(el1, el2, verlierer)
    nächsteEbene.add(parent)
  wenn nächsteEbene.länge == 1
    ausgabe nächsteEbene // nur Wurzel
  sonst
    ausgabe erstelleBaum(nächsteEbene)

running time

The initial construction of the tree takes place in time Θ (k). In each step of the merging, the games must be played anew on the path from the new element to the root. Only one comparison operation is necessary in each level. Since the tree is balanced, the path from the input list to the root contains only Θ (log k) elements. A total of n elements must be transferred. The resulting total running time is therefore Θ (n log k).

example

The following section provides a detailed example of replacement selection and an example of an entire merge process.

Replacement selection

Games are replayed on the way from the bottom up. At each level of the tree, the element stored in the node and the one received from below compete against each other. The winner will continue to be passed up until the entire winner is saved at the end. The loser is saved in the respective node of the tree.

Example for replacement selection

step	action
1	Sheet 1 (overall winner) is replaced by 9, the next element in the associated input list.
2	The game 9 against 7 (loser of the last round) is played again. 7 wins as it is the smaller number. Because of this, 7 is passed up while 9 is stored in the node.
3	The game 7 against 3 (loser of the last round) is played again. 3 wins because it is the smaller number. Because of this, 3 is passed up while 7 is stored in the node.
4th	The game 3 against 2 (loser of the last round) is played again. 2 wins because it is the smaller number. Because of this, 2 is passed up while 3 is stored in the node.
5	The new overall winner, 2, is stored over the root.

Merging

For the actual merging, the smallest element is always removed and replaced with the next element from the input list. Then the games will be played again to the root.

In this example, four sorted arrays are used as input.

{2, 7, 16}
{5, 10, 20}
{3, 6, 21}
{4, 8, 9}

The algorithm is instantiated with the heads of the input lists. A tree of losers is then built from these elements. For merging, the smallest element, 2, is determined by reading the top element in the tree. This value is now removed from the associated input array and replaced by the successor, 7. The games from there to the root are played again, as described in the previous section. The next item to be removed is 3. Starting with the next list item, 6, the games are replayed back to the roots. This is repeated until the total minimum above the root is infinite .

Visualization for the entire algorithm

Runtime analysis

It can be shown that no comparison-based algorithm for k -way mixing can exist which has a faster running time than O (n log k). This can easily be proven by reducing to the comparison-based sorting. If there were a faster algorithm, one could design a comparison-based sorting algorithm that sorts faster than O (n log n). The algorithm divides the input into k = n lists, each containing only one element. Then he merges the lists. If merging were possible under O (n log k), this would contradict the well-known result that a lower limit of O (n log n) applies to sorting in the worst-case scenario.

Parallel mixing

A parallel version of binary merging serves as a building block for a parallel merge algorithm. The following pseudocode demonstrates a parallel divide -and- conquer mixing algorithm (adapted from Cormen et al . ^{: 800} ). It operates on two sorted arrays and and writes the sorted output to the array . The notation denotes the part from from index to exclusive . ${\ displaystyle A}$ ${\ displaystyle B}$ ${\ displaystyle C}$ ${\ displaystyle A [i ... j]}$ ${\ displaystyle A}$ ${\ displaystyle i}$ ${\ displaystyle j}$

algorithm merge(A[i...j], B[k...ℓ], C[p...q]) is
    inputs A, B, C : array
           i, j, k, ℓ, p, q : indices

    let m = j - i,
        n = ℓ - k

    if m < n then
        swap A and B  // ensure that A is the larger array: i, j still belong to A; k, ℓ to B
        swap m and n

    if m ≤ 0 then
        return  // base case, nothing to merge

    let r = ⌊(i + j)/2⌋
    let s = binary-search(A[r], B[k...ℓ])
    let t = p + (r - i) + (s - k)
    C[t] = A[r]

    in parallel do
        merge(A[i...r], B[k...s], C[p...t])
        merge(A[r+1...j], B[s...ℓ], C[t+1...q])

The algorithm starts with either or (depending on which array contains more elements) is split into two halves. Then the other array is split into two parts: the first part contains the values that are smaller than the center of the first array, while the second part contains all values that are equal to or larger than the center. The binary-search subroutine returns the index in where it would be if it were inserted in; this is always a number between and . Finally, each half is shuffled recursively. Since the recursive calls are independent of one another, they can be executed in parallel. A hybrid approach that uses a sequential algorithm for the base case of recursion works well in practice. ${\ displaystyle A}$ ${\ displaystyle B}$ ${\ displaystyle B}$ ${\ displaystyle A [r]}$ ${\ displaystyle B}$ ${\ displaystyle k}$ ${\ displaystyle l}$

The work for mixing two arrays with total elements is . This would be the runtime for a sequential execution of the algorithm, which is optimal since at least elements are copied into the array . In order to calculate the span of the algorithm, it is necessary to set up and solve a recurrence relation. Since the two recursive calls to merge are parallelized, only the more expensive of the two calls has to be considered. In the worst case, the maximum number of elements in a call is because the larger array is perfectly split in half. If the costs for the binary search are now added, we get the following recurrence: ${\ displaystyle n}$ ${\ displaystyle {\ mathcal {O}} (n)}$ ${\ displaystyle n}$ ${\ displaystyle C}$ ${\ textstyle {\ frac {3} {4}} n}$ ${\ displaystyle \ Theta \ left (\ log (n) \ right)}$

${\ displaystyle T _ {\ infty} ^ {\ text {merge}} (n) = T _ {\ infty} ^ {\ text {merge}} \ left ({\ frac {3} {4}} n \ right) + \ Theta \ left (\ log (n) \ right)}$ .

The solution is . So this is the runtime on an ideal machine with an unlimited number of processors ${\ displaystyle T _ {\ infty} ^ {\ text {merge}} (n) = \ Theta \ left (\ log (n) ^ {2} \ right)}$ ^{: 801-802} .

Warning: This parallel mixing routine is not stable . If the same elements are separated when dividing by and , they intertwine in , and swapping of and will destroy the order if the same items are distributed over both input arrays. ${\ displaystyle A}$ ${\ displaystyle B}$ ${\ displaystyle C}$ ${\ displaystyle A}$ ${\ displaystyle B}$

Individual evidence

↑ Steven Skiena: The Algorithm Design Manual , 2nd. Edition, Springer Science + Business Media , 2010, ISBN 1-849-96720-2 , p. 123.
↑ Jyrki Katajainen, Tomi Pasanen, Jukka Teuhola: Practical in-place mergesort . In: Nordic J. Computing . 3, No. 1, 1996, pp. 27-40.
^ Jon Louis Bentley: Programming Pearls , 2nd. Edition, Addison-Wesley, 2000, ISBN 0201657880 , pp. 147-162.
^ ^A ^b Donald Knuth : Chapter 5.4.1. Multiway Merging and Replacement Selection . In: Sorting and Searching (= The Art of Computer Programming ), 2nd. Edition, Volume 3, Addison-Wesley, 1998, ISBN 0-201-89685-0 , pp. 252-255.
↑ ^a ^b Cormen, Thomas H .; Leiserson, Charles E .; Rivest, Ronald L .; Stein, Clifford: Introduction to algorithms . Third ed. MIT Press, Cambridge, Mass. 2009, ISBN 978-0-262-27083-0 .
↑ Victor J. Duvanenko: Parallel Merge . In: Dr. Dobb's Journal . 2011.