Secondary diagonal

Main diagonal (red) and secondary diagonals (blue) of a (4 × 4) matrix

In mathematics , the secondary diagonals of a matrix consist of the matrix elements that lie on an imaginary diagonal line parallel to the main diagonal . Occasionally, however, the opposite diagonals of a matrix are also referred to as "secondary diagonals".

definition

The secondary diagonals of a matrix

${\displaystyle A={\begin{pmatrix}a_{1,1}&a_{1,2}&\ldots &a_{1,n}\\a_{2,1}&a_{2,2}&\ldots &a_{2,n}\\\vdots &\vdots &\ddots &\vdots \\a_{m,1}&a_{m,2}&\ldots &a_{m,n}\end{pmatrix}}}$

consist of those entries whose difference between row and column index results in a constant value not equal to zero, i.e. for the ${\displaystyle a_{i,j}}$

${\displaystyle j-i=k}$

with applies. A secondary diagonal thus consists of matrix entries that lie on a diagonal line running from top left to bottom right. The number indicates the number of the secondary diagonal. The diagonals with the first secondary diagonals of the matrix (or just secondary diagonals), the diagonals with the second secondary diagonals of the matrix and so on. The diagonals with are called lower secondary diagonals and the diagonals with are called upper secondary diagonals. The diagonal with is called the main diagonal of the matrix and is not counted among the secondary diagonals. ${\displaystyle k\neq 0}$ ${\displaystyle |k|}$ ${\displaystyle k=\pm 1}$ ${\displaystyle k=\pm 2}$ ${\displaystyle k<0}$ ${\displaystyle k>0}$ ${\displaystyle k=0}$

example

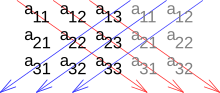
The first two secondary diagonals of the real matrix

${\displaystyle A={\begin{pmatrix}4&3&2&1\\5&4&3&2\\6&5&4&3\\7&6&5&4\end{pmatrix}}}$

consist of the elements and the two second secondary diagonals from the elements and and the two third secondary diagonals from the elements and . The secondary diagonals with the smaller elements are the upper secondary diagonals and those with the larger elements are the lower secondary diagonals. ${\displaystyle 3,3,3}$ ${\displaystyle 5,5,5}$ ${\displaystyle 2,2}$ ${\displaystyle 6,6}$ ${\displaystyle 1}$ ${\displaystyle 7}$

use

Diagonals and counter-diagonals in the rule of Sarrus

Matrices with special occupation patterns with regard to their secondary diagonals are:

• With a diagonal matrix , the entries on all secondary diagonals are zero.
• With a bidiagonal matrix , all entries outside the diagonals and one of the first two secondary diagonals are zero.
• With a tridiagonal matrix , all entries outside the diagonal and the first two secondary diagonals are zero.
• In the case of a pentadiagonal matrix , all entries outside the diagonals, the first two and the two second secondary diagonals, are zero.
• In general, in a band matrix, all entries outside the diagonals and the secondary diagonals are zero from a certain number.

Matrices with one-sided occupation patterns with regard to their secondary diagonals are:

• In the case of a triangular matrix , the entries on all upper secondary diagonals or all lower secondary diagonals are zero.
• With a Hessenberg matrix , the entries on all upper secondary diagonals from the second or on all lower secondary diagonals from the second are equal to zero.

With a symmetrical matrix, the secondary diagonals with the same number match. A matrix in which, as in the example above, the entries on the main diagonal and on all secondary diagonals are constant, is called a Toeplitz matrix .

In Sarrus' rule , the determinant of a matrix is calculated with the help of the main diagonals, two secondary diagonals and three opposite diagonals of the matrix extended by the first two columns. The first upper secondary diagonal also plays an important role in the Jordanian normal form of a matrix. ${\displaystyle (3\times 3)}$

See also

• Diagonal dominant matrix

literature

• Roger A. Horn, Charles R. Johnson: Matrix Analysis . Cambridge University Press, 2012, ISBN 978-0-521-83940-2 .
• Hans Rudolf Schwarz, Norbert Köckler: Numerical Mathematics . 8th edition. Vieweg & Teubner, 2011, ISBN 978-3-8348-1551-4 .

Web links

• Eric W. Weisstein : Diagonal . In: MathWorld (English).