Sum of squares function

The sums of squares function (Engl. Sum of squares function ) is a number theoretic function that specifies how many ways a given natural number as a sum of can be represented squares of integers, all permutations, and sign combinations are counted. It is referred to as . ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle r_{k}(n)}$

definition

The first values ​​of r _k

n	n	r 1 (n)	r 2 (n)	r 3 (n)	r 4 (n)	r 5 (n)	r 6 (n)	r 7 (n)	r 8 (n)
0	0	1	1	1	1	1	1	1	1
1	1	2	4th	6th	8th	10	12	14th	16
2	2	0	4th	12	24	40	60	84	112
3	3	0	0	8th	32	80	160	280	448
4th	2 2	2	4th	6th	24	90	252	574	1136
5	5	0	8th	24	48	112	312	840	2016
6th	2‧3	0	0	24	96	240	544	1288	3136
7th	7th	0	0	0	64	320	960	2368	5504
8th	2 3	0	4th	12	24	200	1020	3444	9328
9	3 2	2	4th	30th	104	250	876	3542	12112
10	2‧5	0	8th	24	144	560	1560	4424	14112
11	11	0	0	24	96	560	2400	7560	21312
12	2 2 ‧3	0	0	8th	96	400	2080	9240	31808
13	13	0	8th	24	112	560	2040	8456	35168
14th	2‧7	0	0	48	192	800	3264	11088	38528
15th	3‧5	0	0	0	192	960	4160	16576	56448
16	2 4	2	4th	6th	24	730	4092	18494	74864
17th	17th	0	8th	48	144	480	3480	17808	78624
18th	2‧3 2	0	4th	36	312	1240	4380	19740	84784
19th	19th	0	0	24	160	1520	7200	27720	109760
20th	2 2 ‧5	0	8th	24	144	752	6552	34440	143136

The function is defined as

${\displaystyle r_{k}(n):=\sum _{\begin{array}{c}a_{1}^{2}+a_{2}^{2}+\cdots +a_{k}^{2}=n\\(a_{1},a_{2},\dots ,a_{k})\in \mathbb {Z} ^{k}\end{array}}1\quad =\quad {\big |}\left\{(a_{1},a_{2},\dots ,a_{k})\in \mathbb {Z} ^{k}\mid a_{1}^{2}+a_{2}^{2}+\cdots +a_{k}^{2}=n\right\}{\big |}}$,

d. H. as the number of possible representations of as the sum of squares of whole numbers with . Be it . ${\displaystyle n}$ ${\displaystyle k}$ ${\displaystyle k\geq 1}$ ${\displaystyle r_{k}(0):=1}$

For example , because there is always 2 sign combinations, and also because of 4 sign combinations. On the other hand, it is because there is no representation of the number 3 as the sum of 2 squares. ${\displaystyle r_{2}(1)=4}$ ${\displaystyle 1=0^{2}+(\pm 1)^{2}=(\pm 1)^{2}+0^{2}}$ ${\displaystyle r_{2}(2)=4}$ ${\displaystyle 2=(\pm 1)^{2}+(\pm 1)^{2}}$ ${\displaystyle r_{2}(3)=0}$

The relationship immediately follows from the definition

${\displaystyle r_{k+m}(n)=\sum _{t=0}^{n}r_{k}(t)\ r_{m}(n-t),}$

from which a recursion formula for efficient calculation can be derived:

${\displaystyle r_{k+1}(n)=r_{k}(n)+2\sum _{t=1}^{\sqrt {n}}r_{k}(n-t^{2}).}$

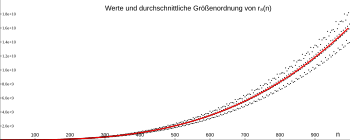
Average order of magnitude

Be it

${\displaystyle R_{k}(x):=\sum _{n=0}^{x}r_{k}(n)=\sum _{a_{1}^{2}+a_{2}^{2}+\dotsb +a_{k}^{2}\leq x}1}$.

This is clearly the number of (integer) grid points in a -dimensional sphere with the radius and therefore approximately equal to the sphere volume. More precisely, it can be derived recursively ${\displaystyle k}$ ${\displaystyle {\sqrt {x}}}$

${\displaystyle R_{k}(x)=V_{k}x^{\frac {k}{2}}+O(x^{\frac {k-1}{2}})}$,

where the constants are the volumes of the -dimensional unit spheres: and is the Landau symbol . ${\displaystyle V_{k}}$ ${\displaystyle k}$ ${\displaystyle V_{2}=\pi ,\;V_{3}={\tfrac {4}{3}}\pi ,\;V_{4}={\tfrac {1}{2}}\pi ^{2},\;\dots }$ ${\displaystyle O(.)}$

The average order of magnitude of is thus , e.g. B. that of . ${\displaystyle r_{k}(n)}$ ${\displaystyle {\tfrac {k}{2}}V_{k}x^{{\tfrac {k}{2}}-1}}$ ${\displaystyle \pi }$ ${\displaystyle r_{2}(x)}$

Generating function

The generating function is obtained as the power of the Jacobian theta function for the special case . This is true ${\displaystyle \vartheta (z,q)}$ ${\displaystyle z=0}$

${\displaystyle \vartheta _{3}(q):=\vartheta (0,q)=\sum _{n=-\infty }^{\infty }q^{n^{2}}=1+2q+2q^{4}+2q^{9}+2q^{16}+\dotsb }$

One gets from it

${\displaystyle (\vartheta _{3}(q))^{k}=\sum _{n_{1},n_{2},\dotsc ,n_{k}}q^{n_{1}^{2}+n_{2}^{2}+\dotsb +n_{k}^{2}}=\sum _{n=0}^{\infty }q^{n}\sum _{n_{1}^{2}+n_{2}^{2}+\dotsb +n_{k}^{2}=n}1=\sum _{n=0}^{\infty }q^{n}\ r_{k}(n)}$

Special cases

Values ​​and average order of magnitude of r ₂ (n)

Values ​​and average order of magnitude of r ₄ (n)

Values ​​and average order of magnitude of r ₈ (n)

Simple formulas result for straight lines , e.g. B. ( ): ${\displaystyle k}$ ${\displaystyle n>0}$

The following applies to: ${\displaystyle k=2}$

${\displaystyle r_{2}(n)=4\sum _{d\mid n \atop d\equiv 1{\pmod {2}}}(-1)^{(d-1)/2}}$

With the help of prime factorization , where the prime factors are the form and the prime factors are the form , another formula results ${\displaystyle n=2^{g}p_{1}^{f_{1}}p_{2}^{f_{2}}\cdots q_{1}^{h_{1}}q_{2}^{h_{2}}\cdots }$ ${\displaystyle p_{i}}$ ${\displaystyle p_{i}\equiv 1{\pmod {4}}}$ ${\displaystyle q_{i}}$ ${\displaystyle q_{i}\equiv 3{\pmod {4}}}$

${\displaystyle r_{2}(n)=4(f_{1}+1)(f_{2}+1)\cdots }$,

when all exponents are even. If at least one is odd, then is . By definition, the number of all Gaussian numbers is also with the norm . ${\displaystyle h_{1},h_{2},\dotsc }$ ${\displaystyle h_{i}}$ ${\displaystyle r_{2}(n)=0}$ ${\displaystyle r_{2}(n)}$ ${\displaystyle n}$

The formula for comes from Carl Gustav Jacob Jacobi and is given as the eightfold sum of all factors that are not divisible by 4 ( Jacobi's theorem ): ${\displaystyle k=4}$ ${\displaystyle n,}$

${\displaystyle r_{4}(n)=8\sum _{d\mid n;4\nmid d}d}$

${\displaystyle r_{4}(n)}$is also the number of all Lipschitz quaternions with the norm . ${\displaystyle n}$

Jacobi also found an explicit formula for : ${\displaystyle k=8}$

${\displaystyle r_{8}(n)=16\sum _{d\mid n}(-1)^{n+d}d^{3}}$

Relationship to the Sierpiński constant

The Limes

${\displaystyle K:=\lim _{n\to \infty }\left(\sum _{k=1}^{n}{\frac {r_{2}(k)}{k}}-\pi \log n\right)}$

exists and is called (after Wacław Sierpiński ) the Sierpiński constant . This can be expressed by the number of circles , the Euler-Mascheroni constant and the gamma function :

${\displaystyle K=\pi (2\gamma +4\log \Gamma ({\tfrac {3}{4}})-\log \pi )}$

See also

• Hurwitz Quaternion
• Two-squares set , three-squares set , four-squares set
• Number theoretic function

Web links

• Eric W. Weisstein : Sum of Squares Function . In: MathWorld (English).

Individual evidence

1. ↑ E. Krätzel: Number theory . VEB Deutscher Verlag der Wissenschaften, Berlin 1981, p. 165 .
2. ↑ E. Krätzel: Number theory . VEB Deutscher Verlag der Wissenschaften, Berlin 1981, p. 197 .