Average order of magnitude

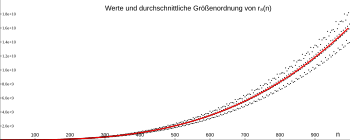
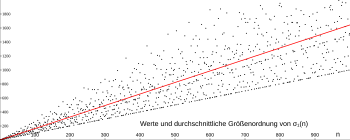
In number theory , the average order of magnitude of a number theoretic function denotes a simpler function that “on average” takes on the same values.

definition

Let it be a number theoretic function. It is said that the average magnitude of is when for the asymptotic equality ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle g}$ ${\displaystyle n\to \infty }$

${\displaystyle \sum _{x\leq n}f(x)\sim \sum _{x\leq n}g(x)}$

applies. It is common practice to choose an approximation function that is continuous and monotonic . But even with this it is by no means clearly determined.

Examples

Values ​​and average order of magnitude of r ₂ (n)

Values ​​and average order of magnitude of r ₄ (n)

Values ​​and average order of magnitude of r ₈ (n)

Values ​​and average order of magnitude of σ ₁

Values ​​and average order of magnitude of ω and Ω

The average order of magnitude of the sum of squares function is determined from the sum ${\displaystyle r_{k}(n)}$

${\displaystyle R_{k}(x):=\sum _{n=0}^{x}r_{k}(n)=\sum _{a_{1}^{2}+a_{2}^{2}+\dotsb +a_{k}^{2}\leq x}1}$.

This is clearly the number of (integer) grid points in a -dimensional sphere with the radius and therefore approximately equal to the sphere volume. More precisely, it can be derived recursively (using Landau's O notation ) ${\displaystyle k}$ ${\displaystyle {\sqrt {x}}}$

${\displaystyle R_{k}(x)=V_{k}x^{\frac {k}{2}}+O(x^{\frac {k-1}{2}})}$,

where the constants are the volumes of the -dimensional unit spheres: ${\displaystyle V_{k}}$ ${\displaystyle k}$

${\displaystyle V_{1}=2,\;V_{2}=\pi ,\;V_{3}={\frac {4}{3}}\pi ,\;V_{4}={\frac {1}{2}}\pi ^{2},\;\dotsc }$

The average order of magnitude of is thus , e.g. B. . ${\displaystyle r_{k}}$ ${\displaystyle r_{k}(n)\sim {\tfrac {k}{2}}V_{k}n^{{\tfrac {k}{2}}-1}}$ ${\displaystyle r_{2}(n)\sim \pi }$

Further examples

• The average magnitude of the Euler's phi function is . ${\displaystyle \varphi (n)}$ ${\displaystyle {\tfrac {6}{\pi ^{2}}}n}$
• The average order of magnitude of the divisor number function is . More precisely applies with Euler's constant ${\displaystyle d(n):=\sigma _{0}(n)}$ ${\displaystyle \ln n}$ ${\displaystyle \gamma }$

${\displaystyle \sum _{x\leq n}d(x)=n\ln n+(2\gamma -1)n+O({\sqrt {n}})}$.

• The average order of magnitude of the divisor function for is with the Riemann zeta function . ${\displaystyle \sigma _{k}(n)}$ ${\displaystyle k>0}$ ${\displaystyle \zeta (k+1)\ n^{k}}$ ${\displaystyle \zeta (s)}$
• The average size of the order , so the number of (not necessarily distinct) prime factors of such also is the number of distinct prime factors . More precisely ( theorem of Hardy and Ramanujan ) ${\displaystyle \Omega (n)}$ ${\displaystyle n}$ ${\displaystyle \omega (n)}$ ${\displaystyle \ln \ln n}$

${\displaystyle \sum _{x\leq n}\omega (x)=n\ln \ln n+B_{1}n+o(n)}$

${\displaystyle \sum _{x\leq n}\Omega (x)=n\ln \ln n+B_{2}n+o(n)}$

with the constants ( Mertens constant ) and ${\displaystyle B_{1}=0{,}26149\dots }$ ${\displaystyle B_{2}=1{,}03465\dots }$

In addition, the average and normal magnitudes are the same for both functions .

• The prime number theorem is equivalent to stating that the average order of magnitude of the Mangoldt function is the same . ${\displaystyle \Lambda (n)}$ ${\displaystyle 1}$
• The prime number theorem is also equivalent to stating that the average magnitude of the Möbius function is the same . ${\displaystyle \mu (n)}$ ${\displaystyle 0}$

See also

• Special number theoretic functions
• Normal order of magnitude

Web links

Eric W. Weisstein : Mertens Constant . In: MathWorld (English).

Individual evidence

1. ↑ E. Krätzel: Number theory . VEB Deutscher Verlag der Wissenschaften, Berlin 1981, p. 132 .
2. ↑ GH Hardy , EM Wright: Introduction to Number Theory . R. Oldenbourg, Munich 1958, p. 300 .
3. ↑ E. Krätzel: Number theory . VEB Deutscher Verlag der Wissenschaften, Berlin 1981, p. 197 .