Divider function

The first values ​​of σ ₀ ... σ ₄

n	=	σ 0 (n)	σ 1 (n)	σ 2 (n)	σ 3 (n)	σ 4 (n)
1	1	1	1	1	1	1
2	2	2	3	5	9	17th
3	3	2	4th	10	28	82
4th	2 2	3	7th	21st	73	273
5	5	2	6th	26th	126	626
6th	2‧3	4th	12	50	252	1394
7th	7th	2	8th	50	344	2402
8th	2 3	4th	15th	85	585	4369
9	3 2	3	13	91	757	6643
10	2‧5	4th	18th	130	1134	10642
11	11	2	12	122	1332	14642
12	2 2 ‧3	6th	28	210	2044	22386
13	13	2	14th	170	2198	28562
14th	2‧7	4th	24	250	3096	40834
15th	3‧5	4th	24	260	3528	51332
16	2 4	5	31	341	4681	69905
17th	17th	2	18th	290	4914	83522
18th	2‧3 2	6th	39	455	6813	112931
19th	19th	2	20th	362	6860	130322
20th	2 2 ‧5	6th	42	546	9198	170898
21st	3‧7	4th	32	500	9632	196964
22nd	2‧11	4th	36	610	11988	248914
23	23	2	24	530	12168	279842
24	2 3 ‧3	8th	60	850	16380	358258
25th	5 2	3	31	651	15751	391251
26th	2-13	4th	42	850	19782	485554
27	3 3	4th	40	820	20440	538084
28	2 2 ‧7	6th	56	1050	25112	655746
29	29	2	30th	842	24390	707282
30th	2‧3‧5	8th	72	1300	31752	872644

In number theory , the divisor function is the function that assigns the sum of its divisors to a natural number , raised to a certain power. It is usually referred to with the Greek letter ${\displaystyle \sigma }$ .

definition

For a natural number is defined: ${\displaystyle n}$

${\displaystyle \!\ \sigma _{k}(n):=\sum _{d|n}d^{k}}$.

The sum extends over all positive factors of , including and . For example, is therefore ${\displaystyle n}$ ${\displaystyle 1}$ ${\displaystyle n}$ ${\displaystyle \sigma _{2}(6)=1^{2}+2^{2}+3^{2}+6^{2}=50.}$

Specializations

• ${\displaystyle d:=\sigma _{0}}$is the number of divisors function ,
• ${\displaystyle \sigma :=\sigma _{1}}$is the partial sum .

properties

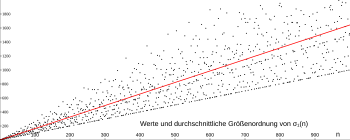
Values ​​and average order of magnitude of σ ₁

Values ​​and average order of magnitude of σ ₂

Values ​​and average order of magnitude of σ ₃

• ${\displaystyle \sigma _{k}}$is multiplicative , ie for prime applies: . ${\displaystyle n,m}$ ${\displaystyle \sigma _{k}(n\cdot m)=\sigma _{k}(n)\cdot \sigma _{k}(m)}$
• If the prime factorization then is ${\displaystyle n}$ ${\displaystyle n=\prod _{i=1}^{r}{p_{i}^{e_{i}}}}$
  • ${\displaystyle \sigma _{k}(n)=\prod _{i=1}^{r}\sum _{j=0}^{e_{i}}{p_{i}^{jk}}}$,
  • ${\displaystyle \sigma _{k}(n)=\prod _{i=1}^{r}{\frac {p_{i}^{k(e_{i}+1)}-1}{p_{i}^{k}-1}}}$for , and   the following applies:  . ${\displaystyle k>0}$ ${\displaystyle k=0}$ ${\displaystyle \sigma _{0}(n)=\prod _{i=1}^{r}(e_{i}+1)}$
• The average order of magnitude of for is , with the Riemann zeta function . ${\displaystyle \sigma _{k}}$ ${\displaystyle k>0}$ ${\displaystyle \sigma _{k}(n)\sim \zeta (k+1)n^{k}}$ ${\displaystyle \zeta (s)}$
• The average order of magnitude of the divisor number function is . More precisely applies with Euler's constant ${\displaystyle d(n):=\sigma _{0}(n)}$ ${\displaystyle \ln n}$ ${\displaystyle C}$

${\displaystyle \sum _{x\leq n}d(x)=n\ln n+(2C-1)n+O({\sqrt {n}})}$.

Series formulas

The following applies in particular : ${\displaystyle \sigma _{0}}$

${\displaystyle \sum _{i=1}^{n}\sigma _{0}(i)=\sum _{i=1}^{n}\left\lfloor {\frac {n}{i}}\right\rfloor }$

This can be made clear in which one the right sum as writes: If one now by substituted, the addend of the sum to be precisely 1 increases, the share. ${\displaystyle \sum _{i=1}^{\infty }\left\lfloor {\frac {n}{i}}\right\rfloor }$ ${\displaystyle n}$ ${\displaystyle n+1}$ ${\displaystyle n+1}$

Two Dirichlet series with the divisor function are: (p. 285, theorem 291)

${\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)}{n^{s}}}=\zeta (s)\zeta (s-a)}$  For  ${\displaystyle s>1,\;s>a+1,}$

which results especially for d ( n ) =  σ ₀ ( n ):

${\displaystyle \sum _{n=1}^{\infty }{\frac {d(n)}{n^{s}}}=\zeta ^{2}(s)}$  For   ${\displaystyle s>1}$

and (p. 292, sentence 305)

${\displaystyle \sum _{n=1}^{\infty }{\frac {\sigma _{a}(n)\sigma _{b}(n)}{n^{s}}}={\frac {\zeta (s)\zeta (s-a)\zeta (s-b)\zeta (s-a-b)}{\zeta (2s-a-b)}}.}$

A Lambert series with the divisor function is:

${\displaystyle \sum _{n=1}^{\infty }\sigma _{a}(n)q^{n}=\sum _{n=1}^{\infty }\sum _{k=1}^{\infty }n^{a}q^{kn}=\sum _{n=1}^{\infty }n^{a}{\frac {q^{n}}{1-q^{n}}}}$

for any complex | q | ≤ 1 and  a .

The divisor function can also be explicitly represented as a series using Ramanujan sums : ${\displaystyle k>0}$

${\displaystyle \sigma _{k}(n)=\zeta (k+1)n^{k}\sum _{m=1}^{\infty }{\frac {c_{m}(n)}{m^{k+1}}}.}$

The calculation of the first values ​​of shows the fluctuation around the "mean value" : ${\displaystyle c_{m}(n)}$ ${\displaystyle \zeta (k+1)n^{k}}$

${\displaystyle \sigma _{k}(n)=\zeta (k+1)n^{k}\left[1+{\frac {(-1)^{n}}{2^{k+1}}}+{\frac {2\cos {\frac {2\pi n}{3}}}{3^{k+1}}}+{\frac {2\cos {\frac {\pi n}{2}}}{4^{k+1}}}+\cdots \right]}$

Identities from the Fourier expansion of Eisenstein series

An essential part of the Fourier expansion of Eisenstein series of weight , straight, are the divider functions . From the relations between the Eisenstein series the values ​​of some convolutions of divisor functions can be derived, for example for all : ${\displaystyle k\geq 4}$ ${\displaystyle \sigma _{k-1}}$ ${\displaystyle n\in \mathbb {N} }$

${\displaystyle 120\sum _{m=1}^{n-1}\sigma _{3}(m)\sigma _{3}(n-m)=\sigma _{7}(n)-\sigma _{3}(n),}$

${\displaystyle 5040\sum _{m=1}^{n-1}\sigma _{3}(m)\sigma _{5}(n-m)=11\sigma _{9}(n)-21\sigma _{5}(n)+10\sigma _{3}(n).}$

swell

1. ↑ Eric W. Weisstein : Divisor Function . In: MathWorld (English).
2. ↑ E. Krätzel: Number theory . VEB Deutscher Verlag der Wissenschaften, Berlin 1981, p. 134 .
3. ↑ Godfrey Harold Hardy , EM Wright: Introduction to Number Theory . R. Oldenbourg, Munich 1958, p. 285, 292 .
4. ↑ E. Krätzel: Number theory . VEB Deutscher Verlag der Wissenschaften, Berlin 1981, p. 130 .
5. ↑ Tom M. Apostol: Modular Functions and Dirichlet Series in Number Theory . 2nd Edition. Springer-Verlag, 1990, p. 140 .