RC6

RC6
developer	Ronald L. Rivest , Matt Robshaw , Ray Sidney , Yiqun Lisa Yin
Released	1997
Derived from	RC5
Key length	128, 192 or 256 bits
Block size	128 bit
structure	Feistel cipher
Round	20th

RC6 ( R ivest C ipher 6 ) is a symmetric block cipher designed by Ronald Rivest and others in 1998 . RC6 is a further development of RC5 and, like this one, uses data-dependent rotations and also the multiplication of data. The theoretical attacks against RC5 known at the time of development should thereby be prevented from the outset.

RC6 was a candidate for the Advanced Encryption Standard (AES) and was one of the finalists there - together with Twofish , Rijndael , MARS and Serpent . It was classified as "sufficiently safe" by the National Institute of Standards and Technology (NIST) - as was Rijndael, who was ultimately elected as an AES. RC6 is simpler than the other finalists, which reduces the chance of implementation errors, and it is also relatively efficient to implement in software.

description

Structure of RC6

RC6 has variable block sizes, numbers of rounds (0–255) and key lengths (0–2040 bits ). A specific choice of these parameters is usually referred to as “RC6- w / r / b ” - w is the length of a data word in bits, r the number of rounds and b the length of the key. A block always consists of four data words, so the block size is bits. The AES candidate was RC6-32 / 20 with a block size of 128 bits, 20 rounds and key lengths of 128, 192 and 256 bits. ${\ displaystyle 4w}$

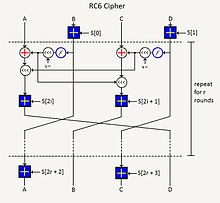
The algorithm uses addition ( ) and multiplication ( ) (each modulo ), bitwise XOR operation ( ) and left rotation ( ), which rotates around bit positions, as primitive operations . ${\ displaystyle A + B}$ ${\ displaystyle A \ cdot B}$ ${\ displaystyle 2 ^ {w}}$ ${\ displaystyle A \ oplus B}$ ${\ displaystyle A \ lll B}$ ${\ displaystyle A}$ ${\ displaystyle B \, {\ bmod {w}}}$

Encryption and decryption

A plain text block in little-endian representation, which consists of the data words A, B, C, D, and the round keys S ₀ to S _{2r + 3 are given} . The logarithm of the word length refers to base 2. The block is encrypted by: ${\ displaystyle \ log w}$ ${\ displaystyle w}$

{\ displaystyle B \ leftarrow B + S_ {0}}

{\ displaystyle D \ leftarrow D + S_ {1}}

{\ displaystyle \ mathbf {for} \; k \ leftarrow 1 \; \ mathbf {to} \; r \; \ mathbf {do:}}

{\ displaystyle t \ leftarrow {\ big (} B \ cdot (2B + 1) {\ big)} \ lll \ log w}

{\ displaystyle u \ leftarrow {\ big (} D \ cdot (2D + 1) {\ big)} \ lll \ log w}

{\ displaystyle X \ leftarrow {\ big (} (A \ oplus t) \ lll u {\ big)} + S_ {2k}}

{\ displaystyle C \ leftarrow {\ big (} (C \ oplus u) \ lll t {\ big)} + S_ {2k + 1}}

{\ displaystyle A \ leftarrow B; \; B \ leftarrow C; \; C \ leftarrow D; \; D \ leftarrow X}

{\ displaystyle A \ leftarrow A + S_ {2r + 2}}

{\ displaystyle C \ leftarrow C + S_ {2r + 3}}

As with RC5, S ₀ and S _{1 are used} for key whitening .

The decryption of a block of ciphertext is the reverse of this algorithm.

Key expansion

P and Q depending on the block size
Block size [bits]	P [hexadecimal]	Q [hexadecimal]
64	B7E1	9E37
128	B7E1 5163	9E37 79B9
256	B7E1 5162 8AED 2A6B	9E37 79B9 7F4A 7C15

The expansion algorithm of RC6, which calculates the round keys S ₀ to S _{2r + 3} , was essentially adopted unchanged from RC5. First, the round keys S _{k are} initialized to a fixed initial state by means of constants . As with RC5, P and Q are odd integers that are generated with Euler's number e and the golden ratio Φ depending on the block size used (table). ${\ displaystyle P, Q}$

{\ displaystyle S_ {0} \ leftarrow P}

{\ displaystyle \ mathbf {for} \; k \ leftarrow 1 \; \ mathbf {to} \; 2r + 3 \; \ mathbf {do:}}

{\ displaystyle S_ {k} \ leftarrow S_ {k-1} + Q}

The secret key is then split into c words up to length w , and the last word is padded with zeros if necessary . The following code then calculates the final round key: ${\ displaystyle L_ {0}}$ ${\ displaystyle L_ {c-1}}$ ${\ displaystyle L_ {c-1}}$

{\ displaystyle k \ leftarrow i \ leftarrow 0}

{\ displaystyle A \ leftarrow B \ leftarrow 0}

{\ displaystyle \ mathbf {do} \; 3 \ cdot \ max {\ big (} 2r + 4, c {\ big)} \; \ mathbf {times:}}

{\ displaystyle A \ leftarrow (S_ {k} + A + B) \ lll 3}

{\ displaystyle B \ leftarrow (L_ {i} + A + B) \ lll (A + B)}

{\ displaystyle S_ {k} \ leftarrow A; \; L_ {i} \ leftarrow B}

{\ displaystyle k \ leftarrow (k + 1) \; {\ bmod {\;}} (2r + 4)}

{\ displaystyle i \ leftarrow (i + 1) \; {\ bmod {\;}} c}

Cryptanalysis

Chosen plaintext

In 2001, Tetsu Iwata and Kaoru Kurosawa from the Tokyo Institute of Technology demonstrated that an idealized RC6 with 4 rounds does not represent a pseudo-random permutation - an attacker with a number of polynomial attempts at encryption can thus distinguish the result of the block cipher from random noise. In the same year, Henri Gilbert, Helena Handschuh, Antoine Joux and Serge Vaudenay presented a statistical attack based on this property, with the help of which - for w = 32 - with ^2,118 pairs of selected plaintexts and their ciphers, bits of the round key for up to Have 13 laps reconstructed. With a memory requirement of ^2,112 and around ^2,122 operations, this attack can also be used as a known plain text attack against 14 rounds. From this attack - which was not practicable due to the requirements - the authors concluded that the 20 rounds of the AES candidate were not excessive.

Known plain text

In 1999, Borst, Preneel, and Vandevalle found that the linear approximation-based attack on RC5 against RC6 that they published was essentially ineffective and that the precautions taken by the RC6 developers were sufficient.

Licensing

RSA was awarded US patents 5,724,428 and 5,835,600 for the RC6 process.

Individual evidence

↑ ^a ^b ^c ^d ^e Ronald L. Rivest , MJB Robshaw, R. Sidney, YL Yin: The RC6 Block Cipher . 1998 ( psu.edu ).
^ Tetsu Iwata, Kaoru Kurosawa: On the Pseudorandomness of the AES Finalists - RC6 and Serpent . In: Lecture Notes in Computer Science . tape 1978/2001 . Springer Berlin / Heidelberg, p. 231 .
^ Henri Gilbert, Helena Handschuh, Antoine Joux, Serge Vaudenay: A Statistical Attack on RC6 . In: Lecture Notes in Computer Science . tape 1978/2001 . Springer Berlin / Heidelberg, p. 1-15 .
^ Johan Borst, Bart Preneel, Joos Vandewalle: Linear Cryptanalysis of RC5 and RC6 . In: Lecture Notes in Computer Science . tape 1636 , no. 1999 . Springer Berlin / Heidelberg, ISSN 1611-3349 , p. 16 .

Web links

[rivest1998-1] Ronald L. Rivest , MJB Robshaw, R. Sidney, YL Yin: The RC6 Block Cipher . 1998 ( psu.edu ).

[iwata2001-2] Tetsu Iwata, Kaoru Kurosawa: On the Pseudorandomness of the AES Finalists - RC6 and Serpent . In: Lecture Notes in Computer Science . tape 1978/2001 . Springer Berlin / Heidelberg, p. 231 .

[gilbert2001-3] Henri Gilbert, Helena Handschuh, Antoine Joux, Serge Vaudenay: A Statistical Attack on RC6 . In: Lecture Notes in Computer Science . tape 1978/2001 . Springer Berlin / Heidelberg, p. 1-15 .

[Borst1999-4] Johan Borst, Bart Preneel, Joos Vandewalle: Linear Cryptanalysis of RC5 and RC6 . In: Lecture Notes in Computer Science . tape 1636 , no. 1999 . Springer Berlin / Heidelberg, ISSN 1611-3349 , p. 16 .