Regular grammar

A regular grammar is a formal grammar of type 3 of the Chomsky hierarchy . The languages ​​produced by such grammars are called regular languages .

definition

A regular grammar (with vocabulary , terminal alphabet , set of non-terminals ( variables ) , production rules and start symbol ) is a context-free grammar , the production rules of which satisfy certain further restrictions. There are two different types of restrictions that specifically define right- regular and left-regular grammars. Since, for practical reasons, one usually adheres to the regular right-hand grammars for applications, one often also says “regular” for short, where one actually means “right-hand regular ” (otherwise regular can mean left-regular or right- regular ). ${\displaystyle G=\left(V,T,P,S\right)}$ ${\displaystyle V}$ ${\displaystyle T}$ ${\displaystyle N:=V\setminus T}$ ${\displaystyle P}$ ${\displaystyle S\in N}$

For production rules , the left side should only ever be a nonterminal symbol regular grammars . This means that every regular grammar is also context-free. In addition, the right-hand side of each rule can contain one or more terminal symbols and at most one non-terminal symbol. All rules with two symbols on their right side must follow the same sequence of terminal and non-terminal symbols. ${\displaystyle w_{1}\to w_{2}\in P}$ ${\displaystyle w_{1}\in N}$

Legal grammars

In legal grammars, the right-hand side of a production may only be the empty word , one or more terminal symbols or one or more terminals followed by a single non-terminal. Derivatives in such grammars grow at the right end of a sentence form . ${\displaystyle w_{2}}$ ${\displaystyle w_{1}\to w_{2}}$

Formally, the condition on the production quantity of a legal grammar can be expressed as follows: ${\displaystyle P}$ ${\displaystyle G}$

${\displaystyle \forall \left(w_{1}\to w_{2}\right)\in P:\left(w_{1}=S\land w_{2}=\varepsilon \right)\lor \left(w_{1}\in N\land w_{2}\in T^{+}\cup T^{+}N\right)}$

${\displaystyle \varepsilon }$stands for the empty word. This is synonymous with

${\displaystyle P\subset \{(S,\varepsilon )\}\cup N\times (T^{+}\cup T^{+}N)}$.

Note that the seemingly stricter requirement

${\displaystyle P\subset \{(S,\varepsilon )\}\cup N\times (T\cup TN)}$

is equal, that is, generates the same formal language. You only have to execute several rules of the type (with terminal characters and non-terminal characters ) one after the other with the help of additional non- terminal characters in order to arrive at and finally also with a non-empty word made up of terminal characters . ${\displaystyle A\to bB}$ ${\displaystyle b}$ ${\displaystyle A,B}$ ${\displaystyle A\rightsquigarrow wB}$ ${\displaystyle A\rightsquigarrow w}$ ${\displaystyle w}$

Left-regular grammars

In the case of left-regular grammars, conversely, the right-hand side of a production may only be the empty word, a terminal symbol or a non-terminal followed by a terminal. So here the derivatives lengthen the sentence forms on the left. ${\displaystyle w_{2}}$

Formally, the conditions are as follows:

${\displaystyle \forall \left(w_{1}\to w_{2}\right)\in P:\left(w_{1}\in N\right)\land \left(w_{2}\in \{\varepsilon \}\cup T^{*}\cup NT^{*}\right)}$

Extended regular grammars

An extended legal grammar follows these rules:

1. B → a - where B is a nonterminal from N, and a is a terminal from Σ.
2. A → B - where A and B are nonterminals of N.
3. A → wB - where A and B are from N and w from Σ ^* .
4. A → ε - where A is from N and ε is the empty word.

Extended left regular grammars are analogous to extended right regular grammars.

Extended regular grammars are equivalent to strictly regular grammars, i. that is, they can also produce exactly all regular languages.

Other spellings

The condition for regular grammars can also be noted more briefly by defining the set of valid production rules:

${\displaystyle P\subseteq N\times (\{\varepsilon \}\cup T\cup TN)}$ (regular legal case)

${\displaystyle P\subseteq N\times (\{\varepsilon \}\cup \Sigma \cup NT)}$ (left-regular case)

For any and in the legal case, only the following pattern of rules are allowed: ${\displaystyle X,Y\in N}$ ${\displaystyle a\in T}$

1. ${\displaystyle X\to aY}$
2. ${\displaystyle X\to a}$
3. ${\displaystyle X\to \varepsilon }$

For left-regular grammars, the following applies instead of the first-mentioned pattern:

1. ${\displaystyle X\to Ya}$

The first production is right or left regular (also called right and left linear). A regular grammar must not mix rules according to both patterns for 1..

Regular languages

A language generated by a regular grammar is called a regular language. For every regular language there is always at least one regular grammar.

The regular languages ​​turn out to be closed under the formation of complement , concatenation , editing , union and formation of the Kleene degree .

Every regular language is also accepted by a suitable deterministic - and then necessarily also by a nondeterministic - finite automaton and is described by a suitable regular expression . Conversely, the languages ​​that a deterministic or nondeterministic finite automaton accepts or that a regular expression describes are also generated by a suitable regular grammar. The fact that in the regular languages ​​the language classes defined by four different formalisms coincide in one class gives them their great importance.

The classes of right-regular and left-regular grammars also coincide: for every left-regular grammar there is a right-regular grammar that generates the same language, and vice versa.

Description of the derivation process

If one follows the course of a derivation in a legal grammar, then all sentence forms that still have a non-terminal symbol at all consist of a word from terminals first, followed by a single non-terminal. The derived word is created step by step by adding a terminal symbol to the right-hand side of the initial terminal word and at the same time changing the final non-terminal.

A deterministic automaton that recognizes ${\displaystyle L_{doremi}}$

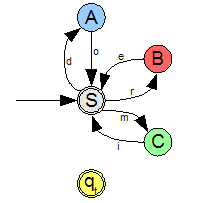
The following legal example grammar with describes the language . ${\displaystyle Ta=\{d,e,i,m,o,r\}}$ ${\displaystyle L_{doremi}=\{do,re,mi\}^{*}}$

${\displaystyle G_{doremi}=(\{S,A,B,C\},T,P,S)}$with the following rules in : ${\displaystyle P}$

${\displaystyle S\to dA|rB|mC|\varepsilon }$

${\displaystyle A\to oS}$

${\displaystyle B\to eS}$

${\displaystyle C\to iS}$

The word has the following derivation: ${\displaystyle domire\in L_{doremi}}$

${\displaystyle S\rightsquigarrow dA\rightsquigarrow \ doS\rightsquigarrow \ domC\rightsquigarrow \ domiS\rightsquigarrow \ domirB\rightsquigarrow \ domireS\rightsquigarrow \ domire}$

This process corresponds to reading the word into a finite automaton . There is a corresponding automaton whose non-terminal symbols correspond to the states and in which there is a transition in the automaton for every rule . The machine for the example grammar is shown in the picture. ${\displaystyle X\to aY}$ ${\displaystyle (X,a,Y)}$

Sources and Notes

1. ↑ Lutz Engelmann (ed.): Small guide to computer science and its application . paetec, Berlin 2000, ISBN 3-89517-615-X .
2. ↑ Some authors alternatively refer to the quadruple as grammar , often other names are also found. ${\displaystyle (N,T,P,S)}$ ${\displaystyle G}$
3. ↑ Peter Rechenberg, Gustav Pomberg (Ed.): Informatik-Handbuch . Hanser, Munich / Vienna 2006, ISBN 978-3-446-40185-3 .
4. ↑ Analogous to Klaus Reinhardt: Priority payment machines and the synchronization of half-track languages ( memento of the original from January 17, 2018 in the Internet Archive ) Info: The archive link was automatically inserted and not yet checked. Please check the original and archive link according to the instructions and then remove this notice. , Faculty of Computer Science at the University of Stuttgart; PhD thesis 1994, page 7 
5. ^ ^{A b} Gordon Pace: Regular Languages. (PDF) In: Computability and Complexity. University of Malta , 2003, p. 22 , accessed April 10, 2016 (English).