Checkerboard paradox

Checkerboard paradox

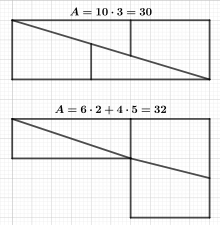
The chessboard paradox or paradox of Loyd and Schlömilch is a pseudo -paradox based on a geometric fallacy. A chessboard or a square with a side length of 8 units of length is cut into four parts, which are then put together to form a rectangle. This rectangle has a length of 13 units of length and a width of 5 units of length and thus an area of ​​65 units of area, which contradicts the fact that the sum of the areas of the four parts (= square area) is only 64 units of area. This contradiction is explained by the fact that the four parts, when they are put together to form the rectangle, only seem to fit together exactly and this difference is barely noticeable with the naked eye. The apparent paradox is named after the American puzzle specialist Samuel Loyd (1841–1911) and the German mathematician Oskar Schlömilch (1832–1901).

Analysis of the sham paradox

The exact representation shows a narrow parallelogram-shaped gap in the rectangle

On closer inspection, the four square parts do not fit together seamlessly; instead, a narrow gap in the form of a parallelogram is created on the diagonal of the rectangle, which is responsible for the increase in area. That the square is actually a parallelogram can be seen, for example, from the calculation of its interior angles. That is, one shows that opposite angles are equal: ${\displaystyle DEBF}$

${\displaystyle {\begin{aligned}\angle FDE&=90^{\circ }-\angle FDG-\angle EDI\\&=90^{\circ }-\arctan \left({\frac {|EI|}{|DI|}}\right)-\arctan \left({\frac {|FG|}{|DG|}}\right)\\&=90^{\circ }-\arctan \left({\frac {5}{2}}\right)-\arctan \left({\frac {3}{8}}\right)\\&=90^{\circ }-\arctan \left({\frac {|FJ|}{|BJ|}}\right)-\arctan \left({\frac {|EH|}{|BH|}}\right)\\&=90^{\circ }-\angle FBJ-\angle EBH\\&=\angle FBE\approx 1.24536^{\circ }\end{aligned}}}$

${\displaystyle {\begin{aligned}\angle DEB&=360^{\circ }-\angle DEI-\angle IEH-\angle EBH\\&=360^{\circ }-\arctan \left({\frac {|DI|}{|EI|}}\right)-90^{\circ }-\arctan \left({\frac {|DG|}{|FG|}}\right)\\&=360^{\circ }-\arctan \left({\frac {2}{5}}\right)-90^{\circ }-\arctan \left({\frac {8}{3}}\right)\\&=360^{\circ }-\arctan \left({\frac {|BJ|}{|FJ|}}\right)-90^{\circ }-\arctan \left({\frac {|BH|}{|EH|}}\right)\\&=360^{\circ }-\angle BFJ-\angle JFG-\angle GFD\\&=\angle DFB\approx 178.75464^{\circ }\end{aligned}}}$

Alternatively, you can check the parallelism of the sides by placing the rectangle in a coordinate system and calculating the gradients or the vector representation of the sides.

The side lengths and diagonals of the parallelogram are:

${\displaystyle |DE|=|FB|={\sqrt {2^{2}+5^{2}}}={\sqrt {29}}}$

${\displaystyle |DF|=|EB|={\sqrt {3^{2}+8^{2}}}={\sqrt {73}}}$

${\displaystyle |EF|={\sqrt {1^{2}+3^{2}}}={\sqrt {10}}}$

${\displaystyle |DB|={\sqrt {5^{2}+13^{2}}}={\sqrt {194}}}$

With Heron's formula the area of ​​half the parallelogram ( ) can be calculated, here the halved perimeter ${\displaystyle \triangle DFG}$

${\displaystyle s={\frac {|EF|+|DE|+|DF|}{2}}={\frac {{\sqrt {10}}+{\sqrt {29}}+{\sqrt {73}}}{2}}}$

and for the area of ​​the entire parallelogram we get:

${\displaystyle {\begin{aligned}F&=2\cdot {\sqrt {s\cdot (s-|EF|)\cdot (s-|DE|)\cdot (s-|DF|)}}\\&=2\cdot {\frac {1}{4}}\cdot {\sqrt {({\sqrt {10}}+{\sqrt {29}}+{\sqrt {73}})\cdot (-{\sqrt {10}}+{\sqrt {29}}{\sqrt {73}})\cdot ({\sqrt {10}}-{\sqrt {29}}+{\sqrt {73}})\cdot ({\sqrt {10}}+{\sqrt {29}}-{\sqrt {73}})}}\\&=2\cdot {\frac {1}{4}}\cdot 2\\&=1\end{aligned}}}$

The parallelogram gap in the rectangle thus corresponds exactly to the increase in area.

generalization

General decomposition with Fibonacci numbers

: , the triangles are almost similar ${\displaystyle {\frac {f_{n-2}}{f_{n}}}\approx {\frac {f_{n-3}}{f_{n-1}}}\Rightarrow \alpha \approx \beta }$
${\displaystyle T_{1},T_{2},T_{3},T_{4}}$

If you consider the lengths of the perpendicular lines that appear in the drawing of the rectangle in the previous section, you get 2, 3, 5, 8 and 13. These are consecutive Fibonacci numbers . The use of the Fibonacci numbers provides a deeper explanation of why the selected route lengths for the division of the square are particularly suitable for the geometric fallacy or the optical illusion and why the increase in area is exactly one unit of area. In addition, one obtains a generalization of the paradox to squares whose side length corresponds to a Fibonacci number. Just as you split the square of side length 8 with the help of the line lengths 8, 5 and 3, you can also split a square of the side length with the help of the line lengths , and (see drawing). ${\displaystyle f_{n}}$ ${\displaystyle f_{n}}$ ${\displaystyle f_{n-1}}$ ${\displaystyle f_{n-2}}$

The Cassini identity applies to Fibonacci numbers :

${\displaystyle f_{n+1}\cdot f_{n-1}-f_{n}^{2}=(-1)^{n}}$

On the basis of this one can see immediately that the difference in area between square and rectangle must always be one unit of area, in particular the following applies to the original checkerboard paradox with : ${\displaystyle f_{6}=8}$

${\displaystyle 13\cdot 5-8^{2}=f_{7}\cdot f_{5}-f_{6}^{2}=(-1)^{6}=1}$

If is odd, the rectangle is not one area unit larger, but smaller. This is due to the fact that in this case there is no narrow gap on the diagonal, but the square parts slightly overlap there. ${\displaystyle n}$

Since the ratio of two consecutive Fibonacci numbers converges very quickly to the golden ratio, the following applies: ${\displaystyle \varphi }$

${\displaystyle {\frac {f_{n}}{f_{n-2}}}={\frac {f_{n}}{f_{n-1}}}\cdot {\frac {f_{n-1}}{f_{n-2}}}\rightarrow \varphi ^{2},\,{\frac {f_{n-2}}{f_{n}}}={\frac {f_{n-2}}{f_{n-1}}}\cdot {\frac {f_{n-1}}{f_{n}}}\rightarrow \varphi ^{-2}}$

The four square parts fit together seamlessly when the parallelogram degenerates into a line and thus coincides with the rectangular diagonal. In this case applies to the angles ${\displaystyle DEBF}$

${\displaystyle \angle IDE=\angle HEB}$, , , , ${\displaystyle \angle DEI=\angle EBH}$ ${\displaystyle \angle FDG=\angle BFJ}$ ${\displaystyle \angle GFD=\angle JBF}$

because it is step angle is at parallels, also so that the triangles , , and all similar to each other. From the equality of the angles, the equality of the associated tangent values ​​follows, those in the rectangle the fractions ${\displaystyle \triangle IED}$ ${\displaystyle \triangle HBE}$ ${\displaystyle \triangle DFG}$ ${\displaystyle \triangle FBJ}$

${\displaystyle {\frac {f_{n-1}}{f_{n-3}}}}$, , And ${\displaystyle {\frac {f_{n}}{f_{n-2}}}}$ ${\displaystyle {\frac {f_{n-3}}{f_{n-1}}}}$ ${\displaystyle {\frac {f_{n-2}}{f_{n}}}}$

correspond. Due to the above convergence we now have:

${\displaystyle {\frac {f_{n}}{f_{n-2}}}\approx {\frac {f_{n-1}}{f_{n-3}}},\,{\frac {f_{n-2}}{f_{n}}}\approx {\frac {f_{n-3}}{f_{n-1}}}}$

This means that the tangent values ​​and the associated angles are almost the same, the triangles are almost similar and the four square parts seem to fit exactly together. Therefore, the Fibonacci numbers are particularly suitable for optical illusion.

history

Paradox by Hooper

The Hooper Paradox is a geometric fallacy that can be seen as a precursor to the Checkerboard Paradox, as it uses the same decomposition figures. However, no square is broken down there and the decomposition is not based on the Fibonacci numbers. William Hooper published the pseudo paradox named after him in 1774 under the title The geometric money in his four-volume work Rational Recreations , initially with an incorrect drawing, which was corrected in the 1783 edition. The paradox does not go back to Hooper himself, because his Rational Recreations was essentially a translation of the Nouvelles récréations physiques et mathétiques by Edmé Gilles Guyot (1706–1786). This four-volume work was published in France in 1769 and contained the same incorrect drawing in its first edition.

The first known publication of the actual chess paradox comes from Oskar Schlömilch and appeared in 1868 as a contribution with the title Ein geometrisches Paradoxon in the journal for mathematics and physics . In 1879 Victor Schlegel published the article Generalization of a Geometric Paradox in the same journal , in which the reference to the Fibonacci numbers was established and used to generalize the construction. The mathematician and author Lewis Carroll also dealt with the chessboard paradox and independently of Schlegl examined a generalization based on the Fibonacci numbers. However, he did not publish his findings, but his undated and incomplete investigation was only discovered later in his estate. The American puzzle inventor Samuel Loyd , according to his own statements, first presented the chessboard paradox at the international chess congress in 1858, later it was part of the work Sam Loyd's Cyclopedia of 5,000 Puzzles, Tricks and Conundrums (1914) published by his son of the same name . This also contains the assembly of the four square parts to form a figure with 63 surface units, which Sam Loyd's son claimed to be his invention. However, this variant can already be found in the article Some postcard puzzles by Walter Dexter from 1901.

literature

• Thomas Koshy: Fibonacci and Lucas Numbers with Applications . Wiley, 2001, ISBN 9781118031315 , pp. 100-108
• Martin Gardner: Mathematics, Magic and Mystery . Courier (Dover), 1956, ISBN 9780486203355 , pp. 129-155
• Franz Lemmermeyer: Mathematics à la carte: elementary geometry at square roots with some historical remarks . Springer 2014, ISBN 9783662452707 , pp. 95–96
• Albrecht Beutelspacher , Bernhard Petri: The golden ratio. Spectrum, Heidelberg / Berlin / Oxford 1996. ISBN 3-86025-404-9 , pp. 91-93
• Jean-Paul Delahaye: Au pays des paradoxes . Humensis, 2014, ISBN 9782842451363
• Greg N. Frederickson: Dissections: Plane and Fancy . Cambridge University Press, 2003, ISBN 9780521525824 , Chapter 23, pp. 268–277 in particular pp. 271–274 ( online update to Chapter 23 )
• Miodrag Petkovic: Famous Puzzles of Great Mathematicians . AMS, 2009, ISBN 9780821848142 , pp. 14, 30-31
• AF Horadam: Fibonacci Sequences and a Geometrical Paradox . In: Mathematics Magazine , Volume. 35, No. 1 (Jan., 1962), pp. 1-11 ( JSTOR )
• David Singmaster: Vanishing Area Puzzles . In: Recreational Mathematics Magazine , No. 1, March 2014
• Colin Foster: Slippery Slopes . In: Mathematics in School , Volume 34, No. 3 (May, 2005), pp. 33–34 ( JSTOR )
• John F. Lamb Jr .: The Rug-cutting Puzzle . In: The Mathematics Teacher , Volume 80, No. 1 (January 1987), pp. 12-14 ( JSTOR )
• Warren Weaver: Lewis Carroll and a Geometrical Paradox . In: The American Mathematical Monthly , Volume 45, No. 4 (Apr. 1938), pp. 234-236 ( JSTOR )
• Oskar Schlömilch : A geometric paradox . In: Journal of Mathematics and Physics , Volume 13, 1868, p. 162
• Victor Schlegel : Generalization of a geometric paradox . In: Journal for Mathematics and Physics , Volume 24, 1879, pp. 123–128

Web links

Commons : Missing square puzzle  - collection of pictures, videos and audio files

• Jigsaw paradox
• Eric W. Weisstein : Dissection Fallacy . In: MathWorld (English).
• Checkerboard paradox