Fast wavelet transform

The fast wavelet transformation, English fast wavelet transform, is an efficient method for calculating a discrete wavelet transformation . It can be compared to using the Fast Fourier Transform to compute the coefficients of a Fourier series .

construction

Analysis filter bank, ${\displaystyle g=a^{-},h=b^{-}}$

Recursive application of an analysis filter bank

A given continuous signal is first converted into a time-discrete sequence of coefficients by orthogonal projection onto a subspace of an orthogonal multiscale analysis . The larger it is, the more precise the approximation achieved. In many cases it is sufficient ${\displaystyle f}$ ${\displaystyle V_{-J}}$ ${\displaystyle s^{(-J)}}$ ${\displaystyle J}$

${\displaystyle s_{n}^{(-J)}:=2^{-J/2}\,f(n/2^{J})}$

to put. Now every low-pass signal becomes a new low-pass signal recursively ${\displaystyle s^{(k)}}$

${\displaystyle s^{(k+1)}={\frac {1}{\sqrt {2}}}(\downarrow 2)(a_{-}*s^{(k)})}$

and the bandpass signal

${\displaystyle d^{(k+1)}={\frac {1}{\sqrt {2}}}(\downarrow 2)(b_{-}*s^{(k)})}$

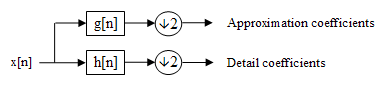
generated. Together these form an analysis filter bank, the operations in which are explained below.

After steps of the recursion the consequences arise ${\displaystyle M}$

${\displaystyle d^{(-J+1)},\dots ,d^{(-J+M)}}$   and   . ${\displaystyle s^{(-J+M)}}$

The aim of this transformation is that the "thin" ones are occupied and can therefore be easily compressed. ${\displaystyle d^{(k)}}$

If the filters and are sufficiently frequency-selective, the output signal was band-limited and the first coefficient sequence was obtained in accordance with the WKS sampling theorem , then the first low-pass result contains all signal components up to half the Nyquist frequency , the band-pass result those above, both times with a sampling rate corresponding to the bandwidth . ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle s_{n}^{(-J)}}$

Analysis and synthesis

The fishbone breakdown in multiscale analysis corresponds to a time-discrete filter bank composed of the low-pass and the band-pass ; a time-discrete signal is divided into a high band and a low band (convolution of sequences). Thereafter, both signals are clocked down (English downsampling ) to ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle x}$ ${\displaystyle b^{-}*x}$ ${\displaystyle a^{-}*x}$

${\displaystyle s=(\downarrow 2)(a^{-}*x)}$   and   . ${\displaystyle d=(\downarrow 2)(b^{-}*x)}$

With is the time-inverted sequence ${\displaystyle a^{-}}$

${\displaystyle a^{-}=\{\dots ,a_{2},a_{1},a_{0},a_{-1},a_{-2},\dots \}}$

designated. Downclocking a sequence means that a new sequence is formed from the terms with an even index,

${\displaystyle (\downarrow 2)(y)=\{\dots ,y_{-4},y_{-2},y_{0},y_{2},y_{4},\dots \}}$.

All of these operations combined result in a computation rule for the analysis filter bank

${\displaystyle s_{n}=\sum _{k}a_{k}\cdot x_{2n+k}}$   and   . ${\displaystyle d_{n}=\sum _{k}b_{k}\cdot x_{2n+k}}$

From orthogonality, it follows that the output signal can be recovered, the first low-pass and band-pass units are and extrapolated in the sample rate, this is called upsampling refers convolved with the scaling and Waveletmasken and then added, ${\displaystyle x}$ ${\displaystyle s}$ ${\displaystyle d}$

${\displaystyle 2x=a*(\uparrow 2)s+b*(\uparrow 2)d}$

or by coefficient

${\displaystyle 2x_{n}=\sum _{k}a_{n-2k}\cdot s_{k}+\sum _{k}b_{n-2k}\cdot d_{k}}$.

The transition from to is called analysis, the inverse synthesis. It can be seen that the transform of a finite signal now has about as many samples as the signal itself, i.e. it contains just as much information. ${\displaystyle x}$ ${\displaystyle (s,d)}$ ${\displaystyle (s,d)}$ ${\displaystyle x}$

Extensions

It is not necessary for the sequences in the analysis filter bank to match those in the synthesis filter bank as above, only then it is not guaranteed that the combination of both filter banks will reconstruct the output signal. If this is the case, one speaks of complete reconstruction (English perfect reconstruction ) or of biorthogonality of the wavelet bases.