Subdifferential

The subdifferential is a generalization of the gradient to non- differentiable convex functions . The subdifferential plays an important role in convex analysis as well as convex optimization .

definition

Let be a convex function. A vector is called a subgradient of at the point if holds for all ${\displaystyle f\colon \mathbb {R} ^{n}\to \mathbb {R} }$ ${\displaystyle g\in \mathbb {R} ^{n}}$ ${\displaystyle f}$ ${\displaystyle x_{0}}$ ${\displaystyle x\in \mathbb {R} ^{n}}$

${\displaystyle f(x)\geq f(x_{0})+\langle g,x-x_{0}\rangle }$,

where denotes the standard scalar product. ${\displaystyle \langle \cdot ,\cdot \rangle }$

The sub- differential is the set of all sub-gradients in the point . ${\displaystyle \partial f(x_{0})}$ ${\displaystyle f}$ ${\displaystyle x_{0}}$

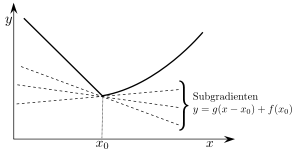
Intuition

Subgradients of a convex function

Intuitively, this definition means that the graph of the function lies everywhere above the straight line that goes through the point and has the slope : ${\displaystyle n=1}$ ${\displaystyle f}$ ${\displaystyle G}$ ${\displaystyle (x_{0},f(x_{0}))}$ ${\displaystyle g}$

${\displaystyle G=\{(x,y)\in \mathbb {R} ^{2}\mid y=g\cdot (x-x_{0})+f(x_{0})\}}$

Since the normal equation of even ${\displaystyle G}$

${\displaystyle -g\cdot (x-x_{0})+1\cdot (y-f(x_{0}))=0}$

is, the normal is on so ${\displaystyle G}$ ${\displaystyle (-g,1)\in \mathbb {R} ^{2}}$

In the general case lies above the hyperplane given by the foot point and the normal . ${\displaystyle n\geq 1}$ ${\displaystyle f}$ ${\displaystyle (x_{0},f(x_{0}))}$ ${\displaystyle (-g,1)\in \mathbb {R} ^{n+1}}$

Because of the separation theorem , the subdifferential of a continuous convex function is not empty anywhere.

example

The subdifferential of the function , is given by: ${\displaystyle f\colon \mathbb {R} \rightarrow \mathbb {R} }$ ${\displaystyle x\mapsto |x|}$

${\displaystyle \partial f(x_{0})={\begin{cases}\{-1\}&x_{0}<0\\\left[-1,1\right]&x_{0}=0\\\{1\}&x_{0}>0\end{cases}}}$

Narrow-mindedness

Be continuous and be limited. Then the amount is limited. ${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} }$ ${\displaystyle X\subset \mathbb {R} ^{n}}$ ${\displaystyle \bigcup _{x_{0}\in X}\partial f(x_{0})}$

proof

Be continuous and be limited. Put where . Adopted is not restricted, then there is for one and one with . Be . So are . We get the estimate ${\displaystyle f\colon \mathbb {R} ^{n}\rightarrow \mathbb {R} }$ ${\displaystyle X\subset \mathbb {R} ^{n}}$ ${\displaystyle \varepsilon :=\sup |f({\overline {U_{1}(X)}})|}$ ${\displaystyle {\overline {U_{1}(X)}}=\{x\in \mathbb {R} ^{n}\mid {\rm {dist}}(x,X)\leq 1\}}$ ${\displaystyle \bigcup _{x_{0}\in X}\partial f(x_{0})}$ ${\displaystyle R:=2\varepsilon }$ ${\displaystyle x_{0}\in X}$ ${\displaystyle g\in \partial f(x_{0})}$ ${\displaystyle \|g\|_{2}>R=2\varepsilon }$ ${\displaystyle x:={\frac {1}{\|g\|_{2}}}g+x_{0}}$ ${\displaystyle x_{0},x\in {\overline {U_{1}(X)}}}$

${\displaystyle g^{T}(x-x_{0})={\frac {1}{\|g\|_{2}}}g^{T}g=\|g\|_{2}>2\varepsilon \geq \left|f(x)-f(x_{0})\right|\geq f(x)-f(x_{0})}$.

${\displaystyle g}$so is not a subgradient. That is a contradiction.

${\displaystyle \Box }$

literature

1. ^ RT Rockafellar Convex analysis 1970., p.214
2. ^ RT Rockafellar Convex analysis 1970., p.215