Treesort

Treesort is a sorting algorithm that was introduced in 1962 by computer scientist Robert Floyd and is one of the predecessors of the Heapsort algorithm .

principle

Treesort receives an input array of elements and outputs them in an output array in ascending order according to their total order relation ("≤"). For this purpose, a buffer of twice the size of the entry is created, of which the second half is initially filled with the unsorted entry. If the whole array is viewed as a binary tree , the rear half represents the entries for the leaf nodes . The front half are the parent nodes, in which the smaller value of the two child nodes is entered in several runs. In addition to the sort key, the position within the leaf nodes is also saved. At the end of a run, the appropriate leaf node is replaced by the value infinite at the position saved in the root node . This means that after each run the root node has the lowest value of the entries in the binary tree, which is then copied into the output array.

The algorithm has an optimal run time by using additional memory. ${\ displaystyle {O} (n \ log n)}$ ${\ displaystyle {O} (n)}$

Pseudocode

The following code describes Floyd's algorithm, which writes the smallest k elements of the n -element array unsorted to the k -element array sorted . At the mbeginning of the function, packe (wert, position)a value is written to the buffer together with its position. The two values are read out again using the functions linkeHälfteand rechteHälfte. The function minimum (x,y)returns the minimum of the two numbers x and y .

 Prozedur Treesort(Unsortiert, n, Sortiert, k)
   m := Array mit Index 1 bis 2n - 1
   für i:= 1 bis n
     m[n+i-1] := packe(Unsortiert[i-1], n+i-1)
   für i:=n-1 bis 1
     m[i] := minimum(m[2i], m[2i+1])
   für j:=1 bis k
     Sortiert[j] := linkeHälfte(m[1])
     i := rechteHälfte(m[1])
     m[i] :=  $\infty$ 
     für i :=  $\lfloor i\div 2\rfloor$  solange i > 0
       m[i] := minimum(m[2i], m[2i+1])

example

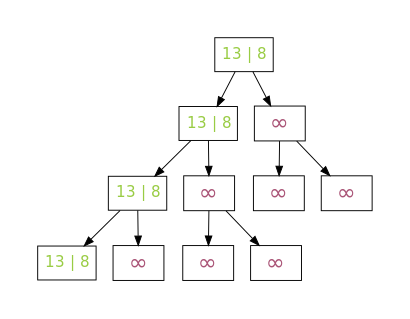
The input array (7, 5, 13, 11, 2, 3) is first saved by Treesort in the buffer together with its position. The array thus has meleven elements and the following entries are at positions 6 to 11:

in m [6] stands (7,6)
in m [7] stands (5,7)
in m [8] stands (13.8)
in m [9] stands (11.9)
in m [10] stands (2,10)
in m [11] stands (3.11)

This state is shown in the first picture as a binary tree. Then the inner nodes are filled from the leaves to the root and the smallest element in the tree is determined, i.e. (2,10). Thus 2 is entered as the first element in the output array and m [10] is set to (second picture). For k = 6, the remaining smallest element is determined in five further loops and transferred to the output array. ${\ displaystyle \ infty}$

initialization
Find the smallest element
Loop: Finding the remaining smallest elements
last step

Individual evidence

↑ US National Institute of Standards and Technology - treesort / 2 xlinux.nist.gov - accessed March 12, 2013
^ Robert W. Floyd : Algorithm 113: Treesort . In: Communications of the ACM . tape 5 , no. 8 , August 1962, p. 434 ( Online [PDF; 725 kB ]).

[1] US National Institute of Standards and Technology - treesort / 2 xlinux.nist.gov - accessed March 12, 2013

[2] Robert W. Floyd : Algorithm 113: Treesort . In: Communications of the ACM . tape 5 , no. 8 , August 1962, p. 434 ( Online [PDF; 725 kB ]).