Heapsort

from Wikipedia, the free encyclopedia
The heapsort algorithm when sorting an array of permuted values. The algorithm consists of two steps; In the preparatory step, the array is rearranged into a binary heap, the tree structure of which is briefly displayed before the actual sorting step.

Heapsort is a sorting process developed in the 1960s by Robert W. Floyd and J. W. J. Williams . Its complexity is in an array of length in the Landau notation expressed in , making it asymptotically optimal for Sort by comparison. Heapsort works in-place , but is not stable . The heapsort algorithm uses a binary heap as the central data structure . Heapsort can be understood as an improvement on Selectionsort and is related to Treesort .

description

The input is an array of items to be sorted. The input to a is first binary heap Max transferred . It follows directly from the heap property that the largest element is now in the first array position. This is swapped with the last array element and the heap array size is reduced by 1 without releasing the memory. The new root of the heap can violate the heap property. The Heapify operation corrected, if appropriate, the heap, so that now the next larger or equal element is in the first array position. The swap, shrink, and heapify steps are repeated until the heap size is 1. The input array then contains the elements in ascending order. In pseudocode : 

heapsort(Array A)
  build(A)
  assert(isHeap(A, 0))
  tmp = A.size
  while (A.size > 1)
    A.swap(0, A.size - 1)
    A.size = A.size - 1
    heapify(A)
    assert(isHeap(A, 0))
  A.size = tmp
  assert(isSorted(A))

When sorting in descending order, a min heap is used instead of the max heap. In a min heap, the smallest element comes first. According to the definition of a binary heap, the sequence of the elements in a heap is determined by a comparison operation (see order relation ), which defines a total order on the elements. In a min heap this is the relation and in a max heap the relation. The pseudocode abstracts from the comparison operation.

The items to be sorted are also known as keys . The input array can contain several data components per index position . In this case, a component must be defined as a sort key on which the comparison operation works. The swap operation swaps complete array entries.

The assert operation in pseudocode documents which properties the array correctly fulfills or must fulfill according to which algorithm steps.

example

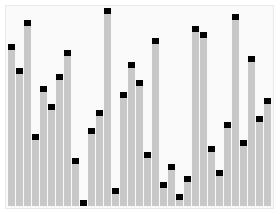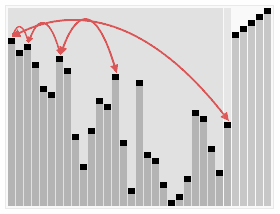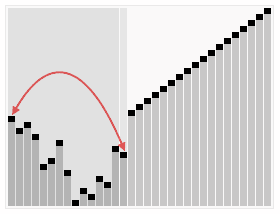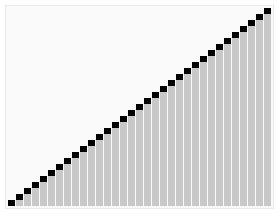
An example of heapsort on a sequence of numbers

The illustration shows the sorting of the sample number sequence 

 23 1 6 19 14 18 8 24 15

shown with the Heapsort algorithm. The individual partial images are arranged chronologically from left to right and from top to bottom. The first part shows the unsorted input and the last shows the sorted output. The transition from the first to the second partial image corresponds to the heapification of the input array. The elements involved in a swap operation are marked in red and with broken arrows, thick double arrows indicate the elements involved in a heapify operation and elements marked in green indicate the already sorted portion of the array. The element indices are shown with small black nodes, each at the bottom left of the element value. A blue background of the array elements indicates the runtime of the heapsort procedure.

The indices correspond to an ascending numbering according to level order, starting with 0. In one implementation of the algorithm, the tree structure is implicit and the array of elements is contiguous, which is indicated by the placement of the element indices in the figure.

Efficiency

It can be shown that the structure of the heap , expressed in Landau notation, can run in steps. In a large, randomly distributed data field (100 to 10 10 data elements), an average of more than 4 but less than 5 significant sorting operations per element are necessary (2.5 data comparisons and 2.5 assignments). This is because a random element will find a suitable parent node with an exponentially increasing probability (60%, 85%, 93%, 97%, ...).

The heapify operation takes steps in the worst case . This is the case with exactly the reverse order. In the average case, about half of the worst case operations and thus steps are also required. Only a field is favorable if its elements almost all have the same value. If, however, only less than approx. 80% of the data are identical, then the runtime already corresponds to the average case. An advantageous arrangement of data with several different values ​​is fundamentally impossible, as this contradicts the heap characteristics.

The worst case set with is largely pre-sorted data because of Heapaufbau de facto represents a gradually complete inversion of the sort order. The most favorable but unlikely case is a data field that has already been sorted the other way round (1 comparison per element, no assignment). The same applies if almost all data is identical.

On heterogeneous data - pre-sorted or not - Heapify dominates at least over 60% of the time, mostly over 80%. Heapsort thus guarantees a total runtime of . Even in the best case, a running time of is required.

A variant of Heapsort requires comparisons in the worst case .

Demarcation

On average, Heapsort is only faster than Quicksort if comparisons on the data to be sorted are very complex and at the same time there is an unfavorable data arrangement for Quicksort, e.g. B. many identical elements. In practice, with unsorted or partially pre-sorted data, quicksort or introsort is faster than heapsort by a constant factor of 2 to 5. However, this is controversially discussed and there are analyzes that see Heapsort in the foreground, both for implementation and information theory considerations. However, the worst-case behavior speaks of the opposite with Quicksort for Heapsort. Introsort, on the other hand, is faster than Heapsort in almost all cases, only 20% to 30% slower in degenerate cases.

Bottom-up heapsort

The most important variant of the heapsort algorithm is bottom-up heapsort, which can often save almost half of the necessary comparison operations and is therefore particularly profitable where comparisons are time-consuming.

Bottom-up heapsort is a sorting algorithm that was introduced in 1990 by Ingo Wegener and others and works better on average than quicksort if comparison operations are weighted sufficiently. It is a variant of Heapsort that is particularly suitable for sorting very large amounts of data if (compared to the necessary swapping operations) a relatively high effort is required per comparison operation.

This variant, however, was already in 1986 analyzed by Svante Carlsson, who eventually found another variant that even a worst-case - running time of only has to compare. This bottom-up heapsort was already discovered by Robert W Floyd , but he was unable to prove the runtime behavior of this variant.

Bottom-up heapsort requires comparisons to sort a sequence of elements in the worst case . On average there are comparisons.

Sorting principle

When sorting with normal heapsort, two comparisons are made for each level when an element is lowered:

  1. Which of the two successor nodes of the element to be lowered is larger?
  2. Is the successor node now determined larger than the element to be lowered?

Since half of a binary tree consists of leaves and, in addition, former leaves with already rather low values ​​are lowered when sorting, it is likely that an element will have to be lowered to or near the leaf level. It can therefore be worthwhile to forego the second comparison and, if there is any suspicion, to lower it to the leaf level.

In a second step, a backward check is made to determine how far the element has to be lifted again. In the best case (very large fields with only a few duplicates ), almost half of the comparisons required can be saved with moderate additional effort.

Bottom-up heapsort is less suitable for sorting smaller fields with a simple numerical comparison operation and when a large number of elements in the field are equivalent. Then the assumption is not correct that it usually has to be lowered to near the leaf level.

algorithm

Specifically, the heapsort algorithm is changed as follows with regard to lowering:

First the path in which the root element is to be sunk is determined. This is done by determining the largest child in each case (path of maximum children). Then this particular path is traversed from bottom to top by the leaf towards the root. Each node visited is compared to determine whether it is larger than the root element to be lowered. If so, the root element is copied to the position of the node visited last and the rest of the path is moved up one level beforehand.

Alternatively, the shift can be carried out from the start on suspicion down to the sheet level and later - if necessary - undone. Where copies can be made relatively cheaply (e.g. because only one pointer is copied), this can be advantageous overall.

example

Heap : [9, 23, 24, 20, 18, 14, 17, 13, 15, 11, 10, 5, 7, 3, 2]

Tree structure: 

            9
       /         \
      23         24
    /   \       /  \
   20   18     14  17
  / \   / \   / \  / \
 13 15 11 10  5  7 3  2

The element 9 must be lowered because it is smaller than at least one successor node. First, the path of the maximum children (starting from the root) is determined. The result is 9 - 24 - 17 - 3 . The algorithm now runs through this path from bottom to top, i.e. 3 -> 17 -> 24 -> 9 . Now the path starting from the leaf node (3) is traversed until a node is found that is greater than 9 . The run ends at 17 . Now all nodes from 17 to the successor node of the root (= 17 -> 24) are moved up one level and node 9 is moved to the position of 17 . As a result, 17 and 24 as successor nodes and 9 as root nodes change their place.

Heap : [24, 23, 17, 20, 18, 14, 9, 13, 15, 11, 10, 5, 7, 3, 2]

Tree structure: 

           24           -------|                      24
       /         \             |                 /         \
      23         17            9                23         17
    /   \       /  \           |               /   \      /   \
   20   18     14      <-------|              20   18    14    9
  / \   / \   / \  / \                       / \   / \   / \  / \
 13 15 11 10  5  7 3  2                     13 15 11 10 5  7  3  2

implementation

Simple example implementation in the programming language C :

 int heapsort_bu( int * data, int n ) // zu sortierendes Feld und seine Länge
 {
   int val, parent, child;
   int root= n >> 1;                  // erstes Blatt im Baum
   int count= 0;                      // Zähler für Anzahl der Vergleiche

   for ( ; ; )
   {
     if ( root ) {                    // Teil 1: Konstruktion des Heaps
       parent= --root;
       val= data[root];               // zu versickernder Wert
     }
     else
     if ( --n ) {                     // Teil 2: eigentliche Sortierung
       val= data[n];                  // zu versickernder Wert vom Heap-Ende
       data[n]= data[0];              // Spitze des Heaps hinter den Heap in
       parent= 0;                     //   den sortierten Bereich verschieben
     }
     else                             // Heap ist leer; Sortierung beendet
       break;

     while ( (child= (parent + 1) << 1) < n )  // zweites (!) Kind;
     {                                         // Abbruch am Ende des Heaps
       if ( ++count, data[child-1] > data[child] )  // größeres Kind wählen
         --child;

       data[parent]= data[child];     // größeres Kind nach oben rücken
       parent= child;                 // in der Ebene darunter weitersuchen
     }

     if ( child == n )                // ein einzelnes Kind am Heap-Ende
     {                                //   ist übersprungen worden
       if ( ++count, data[--child] >= val ) {  // größer als der zu versick-
         data[parent]= data[child];   //   ernde Wert, also noch nach oben
         data[child]= val;            // versickerten Wert eintragen
         continue;
       }

       child= parent;                 // 1 Ebene nach oben zurück
     }
     else
     {
       if ( ++count, data[parent] >= val ) {  // das Blatt ist größer als der
         data[parent]= val;           //   zu versickernde Wert, der damit
         continue;                    //   direkt eingetragen werden kann
       }

       child= (parent - 1) >> 1;      // 2 Ebenen nach oben zurück
     }

     while ( child != root )          // maximal zum Ausgangspunkt zurück
     {
       parent= (child - 1) >> 1;      // den Vergleichswert haben wir bereits
                                      //   nach oben verschoben
       if ( ++count, data[parent] >= val )  // größer als der zu versickernde
         break;                             //   Wert, also Position gefunden

       data[child]= data[parent];     // Rückverschiebung nötig
       child= parent;                 // 1 Ebene nach oben zurück
     }

     data[child]= val;                // versickerten Wert eintragen
   }

   return count;
 }

For comparison purposes, the function returns the number of comparisons made.

Other variants

Smoothsort

Normal heapsort does not sort fields that are already largely presorted faster than others. The largest elements always have to move all the way forward to the top of the heap before they are copied backwards again. Smoothsort changes this by essentially reversing the order of the heap. However, considerable effort is required to maintain the heap status while sorting. Smoothsort takes a linear runtime of to process a presorted array ( best case ) and, like other variants, a runtime of average and worst case , and achieves near linear performance with many near-sorted inputs. However, not all almost sorted sequences are processed optimally.

Ternary heaps

Another optimization uses ternary heaps instead of binary . Instead of binary trees, these heaps are based on trees in which each fully occupied node has 3 children. This allows the number of comparison operations to be reduced by around 3% for a few thousand to a few million elements. In addition, the other costs are significantly reduced. In particular, due to the flatter heap, almost a third fewer elements have to be shifted when heapify.

In a binary heap , an element with comparisons can be lowered by levels and has skipped indexes on average . In a ternary heap , an element with comparisons can be lowered by levels and has skipped indexes on average . If the relative effort is the same for the same range , then applies

, so

At (realistic with almost 1 million elements) the result is 0.977. The value falls below 1 above . In practice, the savings are somewhat greater, u. a. This is because ternary trees have more leaves and therefore fewer elements have to be infiltrated when building the heap .

Overall, sorting with ternary heaps for large fields (several million elements) and a simple comparison operation can save 20% to 30% time. With small fields (up to around a thousand elements), ternary heaps are not worthwhile or are even slower.

n -ary heaps

With even wider trees or shallower heaps , the number of necessary comparison operations increases again. Nevertheless, they can be advantageous because the other effort, especially that for copying elements, is further reduced and the elements are accessed in a more orderly manner, which can increase the efficiency of caches . If only a simple numerical comparison is to be carried out for large fields and write operations are relatively slow, 8 or more children per node can be optimal.

Simple example implementation with heaps of any arity (WIDTH, with WIDTH> = 2) in the programming language C : 

static size_t heapify(int *data, size_t n, size_t WIDTH, size_t root)
{
  assert(root < n);
  size_t count = 0;
  int val = data[root];
  size_t parent = root;
  size_t child = 0;
  assert(parent * WIDTH >= parent); // Overflow-Test
  while ( (child = parent * WIDTH + 1) < n )  // erstes Kind;
  {                                           // Abbruch am Ende des Heaps
    size_t w = n - child < WIDTH ?
      n - child : WIDTH;            // Anzahl der vorhandenen Geschwister

    count += w;

    size_t max = 0;
    for (size_t i = 1; i < w; ++i )  // größtes Kind suchen
      if (data[child+i] > data[child+max])
        max = i;
    child += max;

    if (data[child] <= val)        // kein Kind mehr größer als der
      break;                        //   zu versickernde Wert

    data[parent] = data[child];     // größtes Kind nach oben rücken
    parent = child;                 // in der Ebene darunter weitermachen
  }
  data[parent] = val;               // gesiebten Wert eintragen
  return count;
}

size_t nhsort(int * data, size_t n, size_t WIDTH)
{
  assert(WIDTH > 1);
  if (n < 2)
    return 0;
  size_t m = (n + WIDTH - 2) / WIDTH;  // erstes Blatt im Baum
  int count = 0;                       // Zähler für Anzahl der Vergleiche

  assert(m > 0);
  for (size_t r = m; r > 0; --r)       // Teil 1: Konstruktion des Heaps
    count += heapify(data, n, WIDTH, r-1);
  for (size_t i = n - 1; i > 0; --i) { // Teil 2: eigentliche Sortierung
    int tmp = data[0];                 // Spitze des Heaps hinter den Heap in
    data[0] = data[i];
    data[i] = tmp;                     //   den sortierten Bereich verschieben
    count += heapify(data, i, WIDTH, 0);
  }
  return count;
}

For comparison purposes, the function returns the number of comparisons made.

See also

literature

Web links

Wikibooks: Heapsort  - Implementations in the Algorithm Collection
Commons : Heap sort  - collection of images, videos and audio files

Individual evidence

  1. ↑ Russel Schaffer, Robert Sedgewick: The analysis of heapsort. In: Journal of Algorithms, Volume 15, Issue July 1, 1993. pp. 76-100, ISSN  0196-6774
  2. ↑ Bela Bollobas, Trevor I. Fenner, Alan M. Frieze: On the best case of heapsort. In: Journal of Algorithms, Volume 20, Issue March 2, 1996. pp. 205-217. ISSN  0196-6774
  3. ↑ Gu Xunrang, Zhu Yuzhang: Optimal heapsort algorithm
  4. ^ Paul Hsieh: Sorting revisited. . azillionmonkeys.com. 2004. Retrieved April 26, 2010.
  5. ^ David MacKay: Heapsort, Quicksort, and Entropy . aims.ac.za/~mackay. December 1, 2005. Archived from the original on June 7, 2007. Retrieved April 26, 2010.
  6. ↑ Stefan Hertel: Smoothsort's behavior on presorted sequences . (PDF) In: Information Processing Letters . 16, No. 4, May 13, 1983, pp. 165-170. doi : 10.1016 / 0020-0190 (83) 90116-3 .