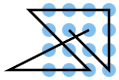
16 point problem

The 16-point problem is a task from the field of practical problem-solving in thought psychology , an extension of the nine-point problem .

task

4 times 4 points

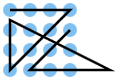
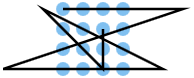
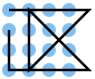
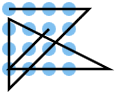
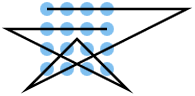
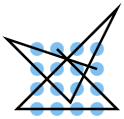
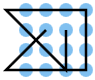
A line consisting of 6 lines should be placed on a point grid of 4 by 4, i.e. 16 points, so that each point is touched by a line at least once.

The problem is an extension of the nine-point problem, which is not easy to solve even with the knowledge that the point grid has to be left.

The solutions outside of Euclidean geometry are discussed in the nine-point problem.

history

The nine-point problem was described in a book by Sam Loyd as early as 1914, and the extension to larger grids is obvious.

In the book Denkspiele der Welt from 1985, the expansion from nine to 16 points is shown and a solution is given.

The 16-point problem was described in Psychology Today in 2009. In 2013, Marco Ribà presented that the puzzle can be solved from any point.

The task was presented as a puzzle of the week in the online edition of Der Spiegel in May 2019 and solved there in the article discussion and subsequently in the Matheplanet forum.

symmetry

Additional solutions can be created for a solution by rotating it by 90 °, 180 °, 270 ° and mirroring and reversing the direction of the solution or combinations thereof. These are not considered to be independent solutions here and are therefore not listed additionally in the table. Additional solutions that are created by extending the start or end line are also not counted separately. Because of the last condition, all the lines listed here begin and end at points that can only be reached by one line. All solutions to the 4 times 4 problem begin with one of the points A1 (solutions 1–26), A2 (solutions 27–39) or B3 (solutions 40–42), since all other grid points are mapped onto these three points by rotating or mirroring them can.

Notation, order

Naming the points

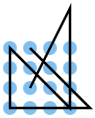
To name the points, the rows are labeled from top to bottom with the letters A – D, the columns with numbers 1–4 from left to right. Point A1 is the corner point at the top left. A solution consists of a sequence of at least 16 points. The lines within the line are separated by a comma. A break point is listed twice, as the end point of the incoming line and as the start point of the outgoing line. The figure shows a corresponding notation for the nine-point problem.

Alternative notations:

Numbers can also be used for the rows, so that the designation corresponds to that of points in the plane in analytical geometry . The point A1 can be selected as (0,0) or (1,1).
Name of the 16 points with hexadecimal digits 0 ... 9, a ... f
Specification of exactly two grid points, first and last point, for each line. Each solution is given by 12 points. Break points are given twice, as the end point of the previous line and the start point of the next line. This notation has the advantage that all solutions are of the same length.

The solutions are sorted here according to the columns and rows of the touched points. So first the solutions that start at point A1 and since there are several, then those that continue at point A2, etc.

A solution that results from a previous solution through a symmetry operation (see above) is not enumerated.

Special solutions

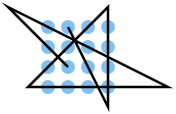
Solutions 19 and 36, category K4, can both be closed, each point is simply touched without kinking at the point, and they have two mirror symmetries along the horizontal and vertical central axes and can be mapped onto themselves by turning 180 °. Many find them particularly elegant.
The solutions for category K1 are often found first. This category also includes the shortest solutions and solution 14, which includes the smallest area outside the grid.

Considerations for other square sizes

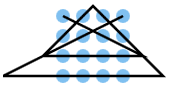
From 3 times 3 points, the required number of lines is given by the formula if the number of points is along one side. ${\ displaystyle 2 (n-1)}$ ${\ displaystyle n}$

This is one line less than a simple "circle inward" solution or scraping all rows in parallel and connecting those lines together .

For the 3 times 3 problem there is exactly one solution under the restrictions mentioned above, which is shown in the table below. With the symmetry conditions selected here, there are 42 solutions for the 4 times 4 problem. For even larger squares, the number of solutions increases sharply.

Complete solution sets can be calculated with computer help. One approach is to connect the grid points and to abort the attempt when the maximum number of lines is exceeded and to select other points when aborting the end of the experiment ( backtracking ). Another approach is to place the specified number of lines so that all points are covered and the lines can be connected to form a line.

A proof that for every square point grid there is no solution with fewer lines was given by Marco Ripá on ViXra . That it is possible with lines is shown by the construction rules below. ${\ displaystyle 2 (n-1)}$

In all solutions, each line touches at least two points and at least one line touches n points, which is the highest possible number. It is believed that this also applies to larger grids.

General solution for n times n

General solution for n> = 3

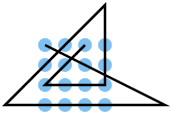
The 3 times 3 solution has a horizontal line end at a corner. Such a solution can be expanded from an n by n to an (n + 1) by (n + 1) solution by adding two lines on the outside. In the picture, the expansion to 4 by 4 is shown by the dark blue points on the right and above (number 14 in the table), which is then expanded to 5 by 5 using the same method on the left and below, with the additional points in purple. From this 5 x 5 solution, there are no more double points achieved in addition to the orange marked points and the grid is no longer left for the solution, which was a specialty of the smaller solutions and gave the name in English: " thinking outside the box"

The 5 by 5 solution shown can be further expanded to a 6 by 6 solution by adding a line at the right and above, etc. For large n, the solution shown is in the middle and is circled.

Solution for n times n, without double points

Solution without double points

There is a design specification that results in a multi-point solution for many large ones. To do this, two separate lines are first created and then connected. (For the designation: N is the letter belonging to n, e.g. for n = 26 is to be used for NZ): ${\ displaystyle n}$

First line train:
- At the bottom right corner Nn (in the picture F6, blue) starting upwards to the top right corner: An (in the picture A6)
- Turning left the diagonal to the bottom left to the corner point bottom left: N1 (in the picture F1)
- Turning further left, each time before an occupied point is reached, until only one point (orange in the picture, E4) is free

Rotated by 180, the same for the remaining triangle at the top left, as a second line:
- Starting at A1 (green in the picture) down to point (N-1) 1 (E1 in the picture)
- Turning left the first upper secondary diagonal to the top right to A (n-1) (in the picture A5)
- Turning further left, each time before an occupied point is reached, until only one point (orange in the picture, B3) is free

Connection of the two lines
- Connect the two remaining free points and continue this line to the extensions of the vertical take-off sections on the right Nn An (in picture F6 A6) and on the left A1 (N-1) 1 (in picture A1 E1).

If n is not divisible by 6 with the remainder of 3, the connecting line has no intersection with other grid points. The solution for the 4 by 4 grid constructed according to this regulation is contained in the table as number 28. The rule does not provide a solution for the 3 by 3 grid: the remaining points are vertically one above the other, so that the connecting line cannot be connected to the two starting lines.

Explanations of the tables

The length indicates the length of the line in the unit of the grid spacing. The connection A1 A2 has the length 1, the diagonal connection A1 B2 the length 1.41.
The rotational symmetry indicates with how many rotations the solution can be mapped onto itself. The maximum value would be the value for the grid, i.e. 4 or symmetry when rotated by 90 °. A symmetry is also counted if it comes about after extending the end lines.
The mirror symmetry indicates whether the solution can be mapped onto itself by mirroring it on the diagonal, the vertical or horizontal central axes.
In the case of multiple points , it is specified how many points are touched by more than one line.
A solution is marked as closable when the extension of the start and end lines intersect. Such solutions have several similar solutions of the same category in the table, because the line can be separated at every corner that protrudes from the grid square.
The left-turn column shows how often the line changes the turning direction when driving through. Coming from the diagonal A1 B2 C3, the continuation C2 C1 would have turned left, the continuation B3 A3 on the right. Each line has 5 changes of direction. A reflection or a reversal of direction converts every left turn into a right turn and vice versa.
A break point is counted when a line does not go straight through a point but changes direction at the point. In the sequence from the 3 times 3 solution: A1 B2 C3, C3 B3 A3, C3 is an inflection point. In the sequence A2 B1, C1 C2 the points are traversed straight, the bend is not on the point grid, but at C0 to the left of the grid.

Table of all solutions to the 3 x 3 problem

number	image	Point sequence	length	Rotational symmetry	Mirror symmetry	Multiple points	lockable	Left turn	Breakpoints
1		A1 B2 C3, C3 B3 A3, A2 B1, C1 C2	12.07	0	1	0	No	3	1

Table of all solutions to the 4 x 4 problem

number	Point sequence	category	length	Rotational symmetry	Mirror symmetry	Multiple points	lockable	Left turn	Breakpoints
1	A1 A2 A3 A4, B3 C1, D1 D2 D3 D4, C4 B2, B1 C2, C3 B4	K8	30.07	0	1	0	No	4th	0
2	A1 A2 A3 A4, A4 B3 C2 D1, D1 C1 B1, B2 C4, D4 D3 D2, D2 C3 B4	K2	22.16	0	0	0	No	0	3
3	A1 A2 A3 A4, A4 B3 C2 D1, D2 C4, B4 B3 B2 B1, C1 D3, D4 C3	K11	31.90	0	1	1	Yes	4th	1
4th	A1 A2 A3 A4, A4 B3 C2 D1, D1 D2 D3 D4, C4 B2, B1 C1 D1, D2 C3 B4	K2	25.58	0	0	2	No	4th	2
5	A1 A2 A3 A4, B4 C1, D1 D2 D3 D4, C4 B2, B1 C2 D3, D3 C3 B3	K10	36.44	0	0	1	No	4th	1
6th	A1 A2 A3 A4, B4 C3, C2 B1, B2 C4, D4 D3 D2 D1, C1 B3	K8	29.25	0	1	0	No	0	0
7th	A1 A2 A3 A4, B4 C3 D2, D2 C2 B2 A2, A2 B3 C4, D4 D3 D2 D1, D1 C1 B1	K1	21.49	0	1	2	Yes	0	3
8th	A1 A2 A3 A4, B4 C3 D2, D1 C1 B1, B1 B2 B3 B4, B4 C4 D4, D3 C2	K1	21.49	0	1	1	Yes	0	2
9	A1 A2 A3 A4, B4 C3 D2, D1 C1 B1, B2 C4, D4 D3 D2 D1, D1 C2 B3	K2	26.58	0	0	2	No	0	1
10	A1 A2 A3 A4, B4 C3 D2, D1 C1 B1, B1 C2 D3, D4 C4 B4, B4 B3 B2	K1	21.90	0	0	1	No	2	2
11	A1 A2 A3 A4, B4 C3 D2, D2 D3 D4, C4 B2, B1 C1 D1, D1 C2 B3	K2	23.16	0	0	0	No	4th	2
12	A1 A2 A3 A4, A4 B4 C4 D4, D3 C2 B1, B1 B2 B3 B4, B4 C3 D2, D1 C1	K1	20.49	0	1	1	Yes	0	3
13	A1 A2 A3 A4, A4 B4 C4 D4, D3 C2 B1, B1 C1 D1, D2 C3 B4, B4 B3 B2	K1	20.49	0	0	1	No	3	3
14th	A1 A2 A3 A4, A4 B4 C4 D4, D4 D3 D2 D1, C1 B2 A3, A3 B3 C3 D3, D3 C2 B1	K1	20.07	0	1	2	Yes	0	4th
15th	A1 A2 A3 A4, C4 D2, D1 C2, C3 D4, D3 C1, B1 B2 B3 B4	K11	34.72	0	0	0	No	0	0
16	A1 A2 A3, A3 B3 C3 D3, D3 D2 D1, C1 B2 A3, A4 B4 C4 D4, D3 C2 B1	K1	22.90	0	1	2	Yes	0	2
17th	A1 B2 C3 D4, C4 A3, A2 B1, C1 D2, D3 B4, A4 B3 C2 D1	K12	27.88	0	1	0	No	5	0
18th	A1 B2 C3 D4, C4 A3, A2 B2 C2 D2, D3 B4, A4 B3 C2 D1, D1 C1 B1	K11	33.73	0	1	2	Yes	4th	1
19th	A1 B2 C3 D4, C4 A3, A2 C1, D1 C2 B3 A4, B4 D3, D2 B1	K4	32.85	2	2	0	Yes	5	0
20th	A1 B2 C3 D4, D4 C4 B4 A4, A2 C1, D1 C2 B3 A4, A3 B1, D1 D2 D3	K5	42.20	0	1	2	No	5	1
21st	A1 B2 C3 D4, D4 D3 D2 D1, D1 C2 B3 A4, A3 B1, C1 C2 C3 C4, B4 A2	K11	31.08	0	1	2	Yes	2	2
22nd	A1 B3, C4 C3 C2 C1, B1 A2, A3 B4, D4 D3 D2 D1, B2 A4	K9	32.67	0	0	0	No	0	0
23	A1 B3, C4 C3 C2 C1, B1 A2, A4 B4 C4 D4, D4 D3 D2 D1, C1 B2 A3	K3	28.37	0	0	2	No	0	1
24	A1 B3, C4 C3 C2 C1, C1 B2 A3, A4 B4 C4 D4, D4 D3 D2 D1, B1 A2	K3	25.96	0	0	1	No	0	2
25th	A1 B3, D4 D3 D2 D1, B1 A2, A4 B4 C4, C4 C3 C2 C1, C1 B2 A3	K3	31.61	0	0	0	No	0	2
26th	A1 B3, D4 D3 D2 D1, C1 B2 A3, A4 B4 C4, C4 C3 C2 C1, B1 A2	K3	29.19	0	0	1	No	0	1
27	A2 A1, B1 C2 D3, D4 C4 B4 A4, A3 B2 C1, D1 D2 D3, D3 C3 B3	K1	23.31	0	1	1	Yes	5	1
28	A2 A3 A4, A4 B3 C2 D1, D1 C1 B1 A1, B2 D3, D4 C4 B4, B4 C3 D2	K2	23.78	0	0	0	No	2	3
29	A2 A3 A4, B4 C3 D2, D1 C1 B1 A1, B2 D3, D4 C4 B4 A4, A4 B3 C2	K2	28.19	0	0	2	No	2	1
30th	A2 A3 A4, B4 C3 D2, D1 C1 B1 A1, B3 D4, D3 C2 B1, B2 C4	K6	36.14	0	0	1	No	0	0
31	A2 B2 C2 D2, D3 B4, A4 C3 B2 D1, D1 C1 B1 A1, A3 C4, D4 C3	K11	36.14	0	0	1	No	2	1
32	A2 B2 C2 D2, D3 B4, A4 C3 B2 D1, D1 C1 B1 A1, A1 B2 C3 D4, C4 A3	K11	30.49	0	1	2	Yes	3	2
33	A2 B3, C3 D2, D1 C1 B1 A1, B2 D3, D4 C4 B4 A4, A3 C2	K8	28.84	0	1	0	No	3	0
34	A2 B3 C4, D4 D3 D2 D1, C1 B2 A3, A4 D3, D2 B1, A1 B4	K7	30.75	0	0	0	No	0	0
35	A2 B3 C4, D4 D3 D2 D1, D1 C1 B1 A1, A1 B2 C3 D4, D4 C4 B4 A1, A3 C2	K2	24.96	0	0	2	No	2	3
36	A2 C1, D1 C2 B3 A4, B4 D3, D2 B1, A1 B2 C3 D4, C4 A3	K4	34.27	2	2	0	Yes	5	0
37	A2 C1, D4 C4 B4 A4, A3 B2 C1, D1 D2 D3, D3 C2 B1, A1 B3	K9	28.26	0	0	0	No	4th	1
38	A2 C3, D3 D2 D1, C1 B2 A3, A1 B4 C4 D4, D3 C2 B1, A1 B3	K9	29.05	0	0	1	No	0	0
39	A2 C3, D4 C4 B4 A4, A3 B2 C1, D1 D2 D3 D4, B3 A1, B1 C2	K9	35.32	0	0	1	No	5	0
40	B2 C1, D1 D2 D3 D4, D4 C4 B4 A4, A4 A3 A2 A1, B1 C2 D3, D3 C3 B3	K1	20.07	0	1	1	Yes	0	3
41	B2 C2 D2, D1 C3 B4, A4 A3 A2 A1, B2 C4, D4 D3 D2 D1, C1 B3	K10	35.20	0	0	1	No	3	1
42	B2 C3 D4, D4 C4 B4 A4, A4 A3 A2 A1, B1 C2 D3, D3 D2 D1, C1 B3	K2	22.54	0	0	0	No	3	3

Individual evidence

^ Pieter van Delft, Jack Botermans, Eugen Oker: Denkspiele der Welt . 5th edition. Heinrich Hugendubel Verlag, Munich 1985, ISBN 3-88034-087-0 , p. 167 .
↑ The Original "Thinking Outside the Box" Puzzle! Retrieved July 30, 2019 .
↑ Marco Ribà: 16 Dots Puzzle (Nine Dots Puzzle General Proof, PART 2). April 27, 2013, accessed April 4, 2020 .
↑ Holger Dambeck, Michael Niestedt (graphic): Puzzle of the week: 16 in one go . In: Spiegel Online . May 26, 2019 ( spiegel.de [accessed July 30, 2019]).
↑ Matroids Matheplanet - Die Mathe Redaktion. Retrieved February 9, 2020 .
↑ Thinking outside the box. In: Chalkdust. March 12, 2018, Retrieved April 4, 2020 (UK English).
↑ Marco Ripà: The 2n-2 Lines Proof of the nxn Points Puzzle. Accessed April 3, 2020 (English).
↑ Il Nine Dots Puzzle Esteso a nXnXn (v). Retrieved April 6, 2020 (Italian).

[1] Pieter van Delft, Jack Botermans, Eugen Oker: Denkspiele der Welt . 5th edition. Heinrich Hugendubel Verlag, Munich 1985, ISBN 3-88034-087-0 , p. 167 .

[2] The Original "Thinking Outside the Box" Puzzle! Retrieved July 30, 2019 .

[3] Marco Ribà: 16 Dots Puzzle (Nine Dots Puzzle General Proof, PART 2). April 27, 2013, accessed April 4, 2020 .

[4] Holger Dambeck, Michael Niestedt (graphic): Puzzle of the week: 16 in one go . In: Spiegel Online . May 26, 2019 ( spiegel.de [accessed July 30, 2019]).

[5] Matroids Matheplanet - Die Mathe Redaktion. Retrieved February 9, 2020 .

[6] Thinking outside the box. In: Chalkdust. March 12, 2018, Retrieved April 4, 2020 (UK English).

[7] Marco Ripà: The 2n-2 Lines Proof of the nxn Points Puzzle. Accessed April 3, 2020 (English).

[8] Il Nine Dots Puzzle Esteso a nXnXn (v). Retrieved April 6, 2020 (Italian).