Biconditional
As biconditional , bisubjunction or material equivalence , sometimes (but ambiguously) just equivalence is called
- a compound statement that is true if and only if its two partial statements have the same truth value, i.e. either both are true or both are false;
- the correspondingly defined truth value function ;
- the linguistic symbol (the junction ) with which these two partial statements are put together.
Spelling and reading
The symbol for the biconditional as a junction is usually the equivalence arrow ↔ , the triple crossbar or the double arrow with two cross lines , and occasionally the tilde ~. (Almost each of these characters is used by different authors and in different contexts with a different meaning, most commonly the tilde for the sentence negation and the double arrow with two cross lines for the metalinguistic equivalence.) In Polish notation , the biconditional is expressed by the capital letter E. .
In natural language there are several ways to express a biconditional , for example the formulations “A if and only if B” (abbreviated as “A iff. B”), “A if and only if B” or “A is” sufficient and necessary for B ”; The phrase “A if and only if B” used in English is also found abbreviated as “A iff B” occasionally even in German-language texts. Any of these phrases are suitable for reading the phrase .
meaning
For the two-valued, truth-functional classical logic , the truth value curve (the truth table ) and thus the meaning of the biconditional is defined by the eq function as follows ("w" stands for "true"; "f" stands for "false"):
| P | Q | |
|---|---|---|
| w | w | w |
| w | f | f |
| f | w | f |
| f | f | w |
In classical logic, the statements and (that is, the conjunction of the conditional and the conditional ) are equivalent , that is, they have the same course of truth values. For this reason, the biconditional is often not introduced as an independent junction, but rather reduced to conjunction and conditional by the following definition:
Let “: =” be the metalinguistic sign for “be defined as” and be and metalinguistic sentence variables, ie placeholders that can stand for any sentences in the logical object language. As a specific example, according to this definition , the expression would be resolved to .
The above equivalence and definability show in particular that the biconditional expresses a sufficient and necessary condition : states that A is a sufficient condition for B and that B is a necessary condition for A; and states that B is a sufficient condition for A and that A is a necessary condition for B.
Examples
- is a biconditional that is always true, that is, a tautology .
- is a biconditional that is never true.
- is a biconditional that can be true or false, depending on the truth of the partial statements A, B, C.
- "The moon is a source of light if and only if Isaac Newton was a German." Is a true biconditional, as well as: "Mars is a planet if the oceans contain salt." This example shows that the paradoxes of the material implication occur analogously with the biconditional: It can be true without there being any substantive connection between the two statements.
Ambiguity for multiple arguments
If more than two arguments are connected by, it is not clear how the formula is meant:
can be the abbreviation for ,
or that they are all either true together or false together:
This is only the same for two arguments. The two truth tables only show the same bit pattern in lines with two arguments:
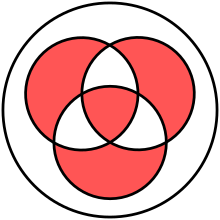
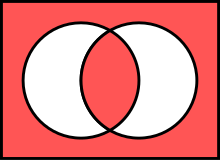
The left Venn diagram below and the rows (AB) in these matrices represent the same operation.
Venn diagrams
Red areas represent the truth (such as in ![]() for and ).
for and ).
|
|
|
Individual evidence
- ↑ both examples taken from Wesley C. Salmon: Logic , Stuttgart: Reclam 1983, ISBN 3-15-007996-9 , page 81