NOR gate

Gate types
	NOT
AND	NAND
OR	NOR
XOR	XNOR

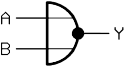
A NOR gate (from English : n ot or - not or , or from English nor - (neither -) nor; also called Peirce function after Charles S. Peirce ) is a logic gate with two or more inputs A, B, ... and an output Y, between which there is a logical NOT OR link . A NOR gate outputs 1 (w) when all inputs are 0 (f). In all other cases, i. H. if at least one input is 1, a 0 is output.

The literature uses the following notations for the NOR operation of variables A and B :

${\displaystyle A\,\operatorname {NOR} \,B\qquad A\downarrow B\qquad \neg \left(A\lor B\right)\qquad A\;\;\!\!{\overline {\lor }}\;\;\!\!B\qquad {\overline {A\lor B}}\qquad {\overline {A+B}}\qquad A\;\;\!\!{\overline {+}}\;\;\!\!B\qquad \neg \left(A+B\right)}$

Overview

function	Circuit symbol			Truth table	Relay logic
	IEC 60617-12	US ANSI 91-1984	DIN 40700 (before 1976)
${\displaystyle Y={\overline {A\vee B}}}$ ${\displaystyle Y=A\;\;\!\!{\overline {\vee }}\;\;\!\!B}$ ${\displaystyle Y={\overline {A+B}}}$ ${\displaystyle Y=A\downarrow B}$ ${\displaystyle Y=A\backslash B}$				A. B. Y = A ⊽ B 0 0 1 0 1 0 1 0 0 1 1 0

realization

The electronic implementation takes place, for example (with positive logic ) with two (or correspondingly more) switches ( transistors ) connected in parallel , which connect output Q to ground (logic 0) as soon as one of them is switched on. If all are off, the ground connection is interrupted and the output Q is at positive potential (logical 1).

• 

  Functional principle of a NOR gate
  ${\displaystyle Q=x\,\operatorname {NOR} \,y}$

• 

  Structure of a NOR gate in RTL technology ( resistor-transistor logic )

• 

  Realization of a NOR gate in CMOS technology (unfavorable to implement, since the two PMOS transistors are connected in series and are already more high-resistance than NMOS transistors with the same chip area ) ${\displaystyle a\;\;\!\!{\overline {\lor }}\;\;\!\!b=a\,\operatorname {NOR} \,b}$

Logic synthesis

According to the following logical equivalence , a NOR operation can also be built up from NAND gates alone :

${\displaystyle x\;\;\!\!{\overline {\lor }}\;\;\!\!y=\left[\left(x\;\;\!\!{\overline {\land }}\;\;\!\!x\right)\;\;\!\!{\overline {\land }}\;\;\!\!\left(y\;\;\!\!{\overline {\land }}\;\;\!\!y\right)\right]\;\;\!\!{\overline {\land }}\;\;\!\!\left[\left(x\;\;\!\!{\overline {\land }}\;\;\!\!x\right)\;\;\!\!{\overline {\land }}\;\;\!\!\left(y\;\;\!\!{\overline {\land }}\;\;\!\!y\right)\right]}$

Logical links and their implementation using NOR gates:

With the Peirce function alone, all two-valued truth functions can be represented, i.e. every Boolean function is equivalent to a formula that only contains the NOR function. Because of this property of functional completeness , the peirce function is called a basis of the two-digit logical functions (another basis is the NAND function).

NOT ( negation , not)	${\displaystyle {\overline {x}}}$	${\displaystyle \equiv }$	${\displaystyle x\;\;\!\!{\overline {\lor }}\;\;\!\!x}$
AND ( conjunction , and)	${\displaystyle x\land y}$	${\displaystyle \equiv }$	${\displaystyle \left(x\;\;\!\!{\overline {\lor }}\;\;\!\!x\right)\;\;\!\!{\overline {\lor }}\;\;\!\!\left(y\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)}$
NAND (not-and)	${\displaystyle x{\overline {\land }}y}$	${\displaystyle \equiv }$	${\displaystyle \left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!x\right)\;\;\!\!{\overline {\lor }}\;\;\!\!\left(y\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\right]\;\;\!\!{\overline {\lor }}\;\;\!\!\left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!x\right)\;\;\!\!{\overline {\lor }}\;\;\!\!\left(y\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\right]}$
OR ( disjunction , or)	${\displaystyle x\lor y}$	${\displaystyle \equiv }$	${\displaystyle \left(x\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\;\;\!\!{\overline {\lor }}\;\;\!\!\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)}$
NOR (not-or)	${\displaystyle x\;\;\!\!{\overline {\lor }}\;\;\!\!y}$	${\displaystyle \equiv }$	${\displaystyle x\;\;\!\!{\overline {\lor }}\;\;\!\!y}$
XOR (Exclusive-Or)	${\displaystyle x\;\;\!\!{\underline {\lor }}\;\;\!\!y}$	${\displaystyle \equiv }$	${\displaystyle \left(x\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\;\;\!\!{\overline {\lor }}\;\;\!\!\left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!x\right)\;\;\!\!{\overline {\lor }}\;\;\!\!\left(y\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\right]}$
XNOR (Exclusive-Not-Or)	${\displaystyle x\;\;\!\!{\overline {\underline {\lor }}}\;\;\!\!y}$	${\displaystyle \equiv }$	${\displaystyle \left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\;\;\!\!{\overline {\lor }}\;\;\!\!x\right]\;\;\!\!{\overline {\lor }}\;\;\!\!\left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\;\;\!\!{\overline {\lor }}\;\;\!\!y\right]}$
implication	${\displaystyle x\rightarrow y}$	${\displaystyle \equiv }$	${\displaystyle \left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!x\right)\;\;\!\!{\overline {\lor }}\;\;\!\!y\right]\;\;\!\!{\overline {\lor }}\;\;\!\!\left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!x\right)\;\;\!\!{\overline {\lor }}\;\;\!\!y\right]}$
	${\displaystyle x\leftarrow y}$	${\displaystyle \equiv }$	${\displaystyle \left[x\;\;\!\!{\overline {\lor }}\;\;\!\!\left(y\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\right]\;\;\!\!{\overline {\lor }}\;\;\!\!\left[x\;\;\!\!{\overline {\lor }}\;\;\!\!\left(y\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\right]}$
equivalence	${\displaystyle x\leftrightarrow y}$	${\displaystyle \equiv }$	${\displaystyle \left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\;\;\!\!{\overline {\lor }}\;\;\!\!x\right]\;\;\!\!{\overline {\lor }}\;\;\!\!\left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!y\right)\;\;\!\!{\overline {\lor }}\;\;\!\!y\right]}$
Verum (always true)	${\displaystyle \top }$	${\displaystyle \equiv }$	${\displaystyle \left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!x\right)\;\;\!\!{\overline {\lor }}\;\;\!\!x\right]\;\;\!\!{\overline {\lor }}\;\;\!\!\left[\left(x\;\;\!\!{\overline {\lor }}\;\;\!\!x\right)\;\;\!\!{\overline {\lor }}\;\;\!\!x\right]}$
Falsum (always wrong)	${\displaystyle \bot }$	${\displaystyle \equiv }$	${\displaystyle \left(x\;\;\!\!{\overline {\lor }}\;\;\!\!x\right)\;\;\!\!{\overline {\lor }}\;\;\!\!x}$

literature

• Ulrich Tietze, Christoph Schenk: Semiconductor circuit technology . 12th edition. Springer, 2002, ISBN 3-540-42849-6 .