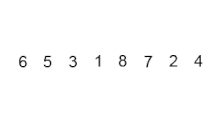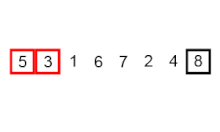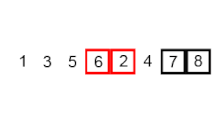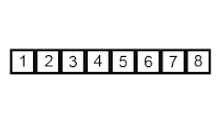Bubble sort

Bubble sort visualization

Bubble sort (also sorting by ascending or exchanging sorting ) is an algorithm that sorts a list of elements based on comparison . This sorting process works in-place , sorts in a stable manner and has a duration of in the worst case ( worst case ) as well as in the average case (average case). The running time is therefore not asymptotically optimal . In practice, bubble sort is rarely used because other methods have better runtime behavior. However, the algorithm plays a role in teaching, as it is considered easy to explain or demonstrate. The algorithm is also suitable for introducing techniques such as step-by-step optimization, runtime or complexity and correctness analysis. ${\ displaystyle \ Theta (n ^ {2})}$

principle

Bubble location on a list of numbers

In the bubble phase, the input list is run through from left to right. In each step the current element is compared with the right neighbor. If the two elements violate the sorting criterion, they are swapped. At the end of the phase, in ascending or descending order, the largest or smallest element of the entry is at the end of the list.

The bubble phase is repeated until the input list is completely sorted. The last element of the previous run no longer has to be considered, since the rest of the input to be sorted no longer contains any larger or smaller elements.

Depending on whether it is sorted in ascending or descending order, the larger or smaller elements such as bubbles in the water (hence the name) rise higher and higher, that is, to the end of the list. Two numbers are always exchanged in "bubbles".

algorithm

To simplify the representation of the algorithm, (greater than) is used below as a comparison relation . As with any sorting method based on comparisons, this can also be replaced by another relation that defines a total order . ${\ displaystyle>}$

The algorithm in its simplest form as pseudocode :

bubbleSort(Array A)
  for (n=A.size; n>1; --n){
    for (i=0; i<n-1; ++i){
      if (A[i] > A[i+1]){
        A.swap(i, i+1)
      } // Ende if
    } // Ende innere for-Schleife
  } // Ende äußere for-Schleife

The input is stored in an array . The outer loop gradually reduces the right limit for the bubble phase, since after each bubble the largest element of the unsorted remainder input is in the rightmost position. The not yet sorted part of the field is run through in the inner loop. Two neighboring data are swapped if they are in the wrong order (i.e. violate the sorting criterion).

However, this simplest variant does not take advantage of the property that after one iteration in which no exchanges took place, no exchanges take place in the remaining iterations either. The following pseudocode takes this into account:

 1 bubbleSort2(Array A)
 2   n = A.size
 3   do{
 4     swapped = false
 5     for (i=0; i<n-1; ++i){
 6       if (A[i] > A[i+1]){
 7         A.swap(i, i+1)
 8         swapped = true
 9       } // Ende if
10     } // Ende for
11     n = n-1
12   } while (swapped)

The outer loop runs through the data to be sorted until no more swaps are necessary.

example

A series of five numbers should be sorted in ascending order.

The numbers in bold are compared. If the left is larger than the right, both are exchanged; the pair of numbers is then marked in blue. In the first pass, the largest number moves all the way to the right. The second pass therefore no longer needs to compare the last and penultimate positions. → Third run: no comparison last / penultimate / penultimate ...

55 07 78 12 42 1. Durchlauf 07 55 78 12 42 07 55 78 12 42 07 55 12 78 42 Letzter Vergleich 07 55 12 42 78 2. Durchlauf 07 55 12 42 78 07 12 55 42 78 Letzter Vergleich 07 12 42 55 78 3. Durchlauf 07 12 42 55 78 Letzter Vergleich 07 12 42 55 78 4. Durchlauf + Letzter Vergleich 07 12 42 55 78 Fertig sortiert.

complexity

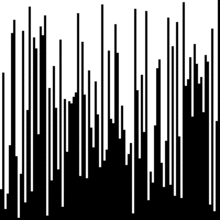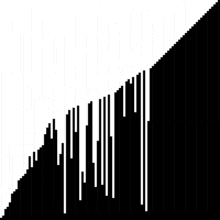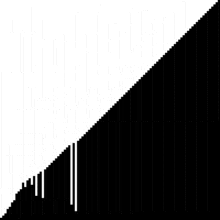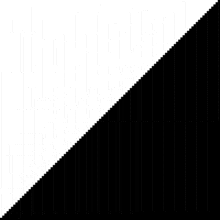
Example of how Bubblesort sorts a list. The list elements are represented by bars. The x -axis indicates where an element is located in the list; the height indicates how big an element is. One frame corresponds to one pass. Start animation

Worst case

Bubblesort has the runtime for lists of length . In the case of the reverse sorted list , a maximum number of interchanges are carried out: in order to move the first (and largest) element to the far right, interchanges are made. General: The movement of the -th element to the place is carried out by interchanges. Adding up all of them results in exchanges as a whole . Since only pairs are exchanged that were also compared beforehand, the algorithm also needs at least as many comparisons. If you look at the pseudocode of the algorithm, you can easily see that none of the instructions can be executed more than times, so this is also the best possible lower bound. ${\ displaystyle {\ mathcal {O}} (n ^ {2})}$ ${\ displaystyle n}$ ${\ displaystyle (n, n-1, \ dotsc, 2,1)}$ ${\ displaystyle {\ tfrac {n \ cdot (n-1)} {2}}}$ ${\ displaystyle n}$ ${\ displaystyle n-1}$ ${\ displaystyle k}$ ${\ displaystyle n}$ ${\ displaystyle nk}$ ${\ displaystyle k}$ ${\ displaystyle {\ tfrac {1} {2}} (n ^ {2} -n) \ in {\ mathcal {O}} (n ^ {2})}$ ${\ displaystyle {\ tfrac {1} {2}} (n ^ {2} -n)}$

Best case

If the list is already sorted, Bubblesort will only go through the list once to determine that the list has already been sorted because no neighboring elements had to be swapped. Therefore, Bubblesort needs steps to process an already sorted list. ${\ displaystyle {\ mathcal {O}} (n)}$

If the elements of the list are already close to the positions they should have after sorting, the runtime is considerably better than . ${\ displaystyle {\ mathcal {O}} (n ^ {2})}$

Average case

The expected number of comparisons for a randomly chosen permutation of the list is ${\ displaystyle (1,2, \ dotsc, n)}$

{\ displaystyle {\ frac {1} {2}} \ left (n ^ {2} -n \ cdot \ ln n - (\ gamma + \ ln (2) -1) \ cdot n \ right) + {\ mathcal {O}} ({\ sqrt {n}})}

,

where denotes the Euler-Mascheroni constant ; the expected number of swaps is . ${\ displaystyle \ gamma}$ ${\ displaystyle {\ tfrac {1} {4}} (n ^ {2} -n)}$

Demarcation

Even if the bubble sort is not asymptotically optimal, it can be used for small inputs, since the constant runtime factors of a sorting algorithm dominate for small ones, which are small for bubble sort. One use case would be the use of bubble sort within a recursive sorting process in order to reduce the number of recursions. ${\ displaystyle n}$

If the elements of a field or a list (up to a certain number) are already sorted with a high probability, bubble sort is suitable, as this is the best case in which the algorithm has a linear runtime. In contrast, other efficient sorting methods, such as e.g. B. Quicksort , or asymptotically optimal methods, such as Mergesort , a best case of . ${\ displaystyle {\ mathcal {O}} (n \ log n)}$

From this point of view, bubble sort competes with insertion sort , whose best case is an already sorted sequence and which has the same complexity as bubble sort (as in the average and worst case). The following applies to both sorting methods: They are stable and work in-place. Depending on the implementation, however, insertion sort has lower constant runtime factors than bubble sort.

Hares and turtles

The position of the elements before sorting is decisive for the sorting effort of Bubblesort. Large elements at the beginning do not have a negative effect, as they are quickly swapped backwards; however, small elements at the end are slow to move forward. That is why the elements that are swapped quickly are called rabbits and the slow ones are called turtles .

Combsort (also known as Gapsort) is the fastest algorithm based on bubblesort. In contrast to Bubblesort, elements that are far from each other are compared and exchanged in order to avoid the dilemma of slowly moving elements. Its duration is also in the worst case and in the best case (Bubblesort:) . Combsort thus achieves the same level of complexity as Quicksort in the worst and best cases . ${\ displaystyle {\ mathcal {O}} (n ^ {2})}$ ${\ displaystyle {\ mathcal {O}} (n \ log {\ sqrt {(}} n))}$ ${\ displaystyle {\ mathcal {O}} (n)}$

Cocktail sort (also called Shakersort) is an alternating sorting algorithm that lets the elements move from the left to the right and from the right to the left. This also counteracts the problem of elements moving slowly forward. Because of the alternation, this algorithm is also called bidirectional bubble sort. In the worst case, its runtime, like that of Bubblesort, is in . ${\ displaystyle {\ mathcal {O}} (n ^ {2})}$

In 2009 Oyelami OM published an optimized version of Bubblesort, which avoids the worst case for fields / lists sorted in reverse order. Due to the associated sorting over distance, the algorithm it uses is no longer stable. Based on the "bubbleSort3" above, an optimized "bidirectional bubble sort" is illustrated below using the "papyrus script function". Float [] a is the pointer to an array with floating point numbers. The two integer parameters represent the flexible sorting area for the array (start value “L”, end value “R”). Assuming the array has 99 elements and starts at 0, then L = 0 and R = 99 must be set in order to sort it completely.

 '''FUNCTION''' SortByBubble3(Float[] a, Int L, Int R)
 1
 2  float X  ; pivot element
 3  float f  ; temp element for swap
 4  int m  ; last swap position
 5  int i  ; counter
 6; ------------------------ round1: suggested by Oyelami
 7  i = L
 8  m = R
 9 '''WHILE''' (i < m) ; to avoid worst-case by using an array sorted in reverse order
 10  X = a[i]
 11  f = a[m]
 12  '''IF''' (X > f)
 13   a[m] = X
 14   a[i] = f
 15  '''ENDIF'''
 16  i = i + 1
 17  m = m - 1
 18 '''ENDWHILE'''
 19; ----------------------- round2: optimized bi-directional BubbleSort
 20 '''WHILE''' (L < R)
 21  X = a[L]
 22  m = L - 1    ; init "m" out of sorting range related to Left bound
 23  i = L + 1
 24  '''WHILE''' (i <= R) ; -- BottomUp loop -- sorts to maximum at the end
 25   f = a[i]
 26   '''IF''' (X <= f)
 27    X = f   ; no exchange: set "pivot" to follower element
 28   '''ELSE'''
 29    a[i] = X  ; \ swap two elements
 30    m = i - 1  ; - update "last swap" position
 31    a[m] = f  ; / and keep current "pivot" for next comparison
 32   '''ENDIF'''
 33   i = i + 1  ; i++
 34  '''ENDWHILE'''
 35;         -------------
 36  R = R - 1   ; R--
 37  '''IF''' (R > m)
 38   '''IF''' (L < m)
 39    R = m   ; shrink the Right bound as much as possible
 40   '''ELSE'''
 41    R = L ; no swap last time, break the loop!
 42   '''ENDIF'''
 43  '''ENDIF'''
 44;          ==============
 45  X = a[R]
 46  m = R + 1    ; init "m" out of sorting range related to Right bound
 47  i = R - 1
 48  '''WHILE''' (i >= L) ; -- TopDown loop -- sorts to minimum on start
 49   f = a[i]
 50   '''IF''' (X >= f)
 51    X = f   ; no exchange: set "pivot" to follower element
 52   '''ELSE'''
 53    a[i] = X  ; \ swap two elements
 54    m = i + 1  ; - update "last swap" position
 55    a[m] = f  ; / and keep current "pivot" for next comparison
 56   '''ENDIF'''
 57   i = i - 1  ; i--
 58  '''ENDWHILE'''
 59  L = L + 1   ; L++
 60  '''IF''' (L < m)
 61   '''IF''' (R > m)
 62    L = m
 63   '''ELSE'''
 64    L = R ; no swap last time, break the loop!
 65   '''ENDIF'''
 66  '''ENDIF'''
 67 '''ENDWHILE'''
 68 '''ENDFUNCTION'''

literature

Thomas H. Cormen, Charles E. Leiserson , Ronald L. Rivest , Clifford Stein: Introduction to Algorithms . 2nd Edition. MIT Press, Cambridge (Massachusetts) 2001, ISBN 0-262-03293-7 , pp. 38 .
Donald E. Knuth : The Art of Computer Programming : Volume 3 Sorting and Searching . 2nd Edition. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0 , pp. 106-110 .

Web links

Commons : Bubblesort - collection of images, videos and audio files

Individual evidence

^ Donald E. Knuth : The Art of Computer Programming : Volume 3 Sorting and Searching . 2nd Edition. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0 , pp. 108-109 .

[1] Donald E. Knuth : The Art of Computer Programming : Volume 3 Sorting and Searching . 2nd Edition. Addison-Wesley, Reading MA 1997, ISBN 0-201-89685-0 , pp. 108-109 .