Discriminant analysis

The discriminant analysis is a method of the multivariate procedure in statistics and serves to differentiate between two or more groups, which are described with several characteristics (also variables). She can check groups for significant differences in their characteristics and identify suitable or unsuitable characteristics. It was first described by RA Fisher in 1936 in The use of multiple measurements in taxonomic problems .

Discriminant analysis is used in statistics and machine learning to achieve a good representation of features through spatial transformation , and serves as a classifier ( discriminant function ) or for dimension reduction. The discriminant analysis is related to the principal component analysis (PCA), which should also find a good display option, but in contrast to this, it takes into account the class membership of the data.

Problem

We consider objects that each belong to exactly one of several similar classes. It is known to which class each individual object belongs. Characteristics of each object are observed. From this information, linear boundaries between the classes should be found in order to be able to assign objects whose class membership is unknown to one of the classes later. The linear discriminant analysis is therefore a classification method .

Examples:

• Borrowers can e.g. B. be divided into creditworthy and not creditworthy. When a bank customer applies for a loan, the bank tries to determine the customer's future solvency and willingness to pay on the basis of characteristics such as income level, number of credit cards, length of employment at the last job, etc.
• Customers of a supermarket chain can be classified as brand buyers and non-name buyers. Possible characteristics would be the total annual expenditure in these shops, the share of branded products in the expenditure, etc.

At least one statistical, metrically scaled feature can be observed on this object . This feature is interpreted as a random variable in the model of discriminant analysis . There are at least two different groups (populations, general populations ). The object comes from one of these populations. The object is assigned to one of these basic populations by means of an assignment rule, the classification rule. The classification rule can often be given by a discriminant function. ${\displaystyle X}$ ${\displaystyle X}$

Classification with known distribution parameters

For a better understanding, the procedure is explained using examples.

Maximum likelihood method

→ Main article : Maximum likelihood method

One method of assignment is the maximum likelihood method: the object is assigned to the group whose likelihood is greatest.

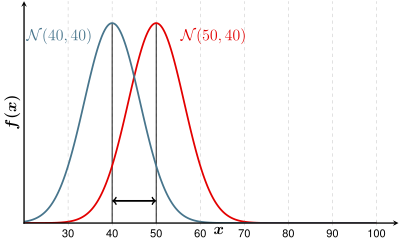
One feature - two groups - equal variances

example

A nursery has the opportunity to buy a large number of seeds of a certain variety of carnations cheaply. In order to dispel the suspicion that these are old, overlaid seeds, a germ test is made. So you sow 1 g of seeds and count how many of these seeds germinate. It is known from experience that the number of germinating seeds per 1 g of seed is almost normally distributed . With fresh seeds (Population I) an average of 80 seeds germinate, with old ones (Population II) there are only 40 seeds.

• Population I: The number of fresh seeds that germinate is distributed as ${\displaystyle X_{I}\sim N(80;10^{2}),}$
• Population II: The number of old seeds that germinate is distributed as ${\displaystyle X_{II}\sim N(40;10^{2}),}$

The germ sample has now

${\displaystyle x=70}$

surrender. The graph shows that this sample has the greatest likelihood of population I. So you classify this germ sample as fresh.

The graphic shows that the classification rule ( decision rule ) can also be specified:

Assign the object to population I when the distance from to the expected value is smallest, or when ${\displaystyle x}$ ${\displaystyle \mu _{I}}$

${\displaystyle |x-\mu _{I}|<|x-\mu _{II}|}$

is.

The point of intersection of the distribution densities (at ) thus corresponds to the decision limit. ${\displaystyle x=60}$

Desirable distribution properties of the features

Same variances

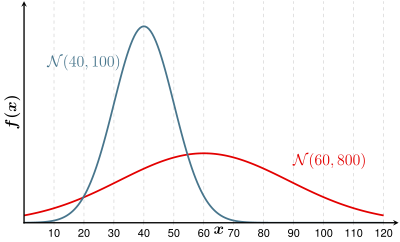
The characteristics of the two groups should have the same variance . With different variances, there are several assignment options.

Different group variances

In the graphic above, two groups with different variances are shown. The flat normal distribution has a greater variance than the narrow, high one. One can see how the variance of group I “undermines” the normal distribution of group II. If, for example , this resulted in the sample, the seeds would have to be classified as fresh, since the probability density for group I is greater than for group II. ${\displaystyle x=10}$

In the “standard model” of discriminant analysis, the same variances and covariances are assumed.

Great intergroup variance

The variance between the group mean values , the intergroup variance , should be large, because then the distributions do not mix: The separation of the groups is sharper.

Worse: Small variance between groups	Better: Large variance between the groups

Small intra-group variance

The variance within a group, the intra- group variance , should be as small as possible, then the distributions do not mix, the separation is better.

Worse: Great variance in a group	Better: Small variance in a group

Multiple features - two groups - same covariance matrices

The object of interest can have several features to be observed . A random vector is obtained here as a model distribution structure . This vector is distributed with the expected value vector and the covariance matrix . The concrete implementation is the feature vector , the components of which contain the individual features . ${\displaystyle x_{j}(j=1,\dots ,m)}$ ${\displaystyle X}$ ${\displaystyle \mu }$ ${\displaystyle \Sigma }$ ${\displaystyle x}$ ${\displaystyle x_{j}}$

In the case of two groups, analogously to the above, the observed object is assigned to the group in which the distance between the feature vector and the expected value vector is minimal. The Mahalanobis distance is used here, partially transformed, as a measure of distance. ${\displaystyle x}$

example

In a large amusement park, the spending behavior of visitors is determined. In particular, they are interested in whether the visitors will spend the night in a park-owned hotel. Every family has total expenses (characteristic ) and expenses for souvenirs (characteristic ) up to 4 p.m. The marketing management knows from many years of experience that the corresponding random variables and together are approximately normally distributed with the variances 25 [€ ² ] and the covariance [€ ² ]. With regard to hotel bookings, consumers can be divided into two groups I and II in terms of their spending behavior, so that the known distribution parameters can be listed in the following table: ${\displaystyle x_{1}}$ ${\displaystyle x_{2}}$ ${\displaystyle X_{1}}$ ${\displaystyle X_{2}}$ ${\displaystyle Cov_{12}=20}$

group	Complete edition	Spending on souvenirs
	Expected value ${\displaystyle E(X_{1})}$	Expected value ${\displaystyle E(X_{2})}$	Variances of and ${\displaystyle X_{1}}$ ${\displaystyle X_{2}}$
Hotel booker I	70	40	25th
No hotel bookers II	60	20th	25th

For group I, the random vector is multivariate normally distributed with the expected value vector

${\displaystyle \mu _{I}={\begin{pmatrix}70\\40\end{pmatrix}}}$

and the covariance matrix

${\displaystyle \Sigma _{I}={\begin{pmatrix}25&20\\20&25\end{pmatrix}}}$

The same applies to group II.

The populations of the two groups are indicated in the following graphic as dense point clouds. The spending on souvenirs is called luxury spending. The pink point stands for the expected values ​​of the first group, the light blue for group II.

Another family visited the theme park. She spent a total of € 65 until 4 p.m. and € 35 on souvenirs (green dot in the graphic). Should you have a hotel room ready for this family?

A look at the graphic already shows that the distance between the green point and the expected value vector of group I is minimal. Therefore, the hotel management suspects that the family will take a room.

For the Mahalanobis distance

${\displaystyle d_{I}(x)=d(x,\mu _{I})=(x-\mu _{I})^{T}\Sigma ^{-1}(x-\mu _{I}).}$

of the feature vector to the center of group I is calculated ${\displaystyle x}$

${\displaystyle d_{I}(x)={\begin{pmatrix}65-70;&35-40\end{pmatrix}}{\begin{pmatrix}0{,}111&-0{,}089\\-0{,}089&0{,}111\end{pmatrix}}{\begin{pmatrix}65-70\\35-40\end{pmatrix}}=1{,}11}$

and from to the center of group II ${\displaystyle x}$

${\displaystyle d_{II}(x)={\begin{pmatrix}65-60;&35-20\end{pmatrix}}{\begin{pmatrix}0{,}111&-0{,}089\\-0{,}089&0{,}111\end{pmatrix}}{\begin{pmatrix}65-60\\35-20\end{pmatrix}}=14{,}44.}$

Multiple features - multiple groups - same covariance matrices

The analysis can be based on more than two populations. Here too, analogously to the above, the object is assigned to the population for which the Mahalanobis distance of the feature vector to the expected value vector is minimal. ${\displaystyle x}$

(Fisherman's) discriminant function

In practice, it is cumbersome to determine the Mahalanobis distance for every feature to be classified. Allocation is easier using a linear discriminant function . Based on the decision rule

"Assign the object to group I if the distance between the object and group I is smaller":

${\displaystyle d_{II}(x)>d_{I}(x)}$

By transforming this inequality, the decision rule results with the help of the discriminant function : ${\displaystyle f(x)}$

"Assign the object to group I, if applies":

${\displaystyle f(x)>0}$.

The discriminant function is calculated in the case of two groups and the same covariance matrices as

${\displaystyle f(x)=(x-{\tfrac {1}{2}}(\mu _{I}+\mu _{II}))^{T}\Sigma ^{-1}(\mu _{I}-\mu _{II})={\tfrac {1}{2}}(d_{II}(x)-d_{I}(x))}$

The discriminant function also results as an empirical approach if one maximizes the variance between the groups and minimizes the variance within the groups. This approach is called Fisher's discriminant function because it was introduced by RA Fisher in 1936.

Bayesian Discriminant Analysis

So far it has been assumed that the groups in the population are of the same size. But this is not the norm. Belonging to a group can also be viewed as random. The probability with which an object belongs to a group is called the a priori probability . In the case of groups, the linear discriminant rule is based on the assumption that the group has a multivariate normal distribution with an expected value and covariance matrix that is the same in all groups, i.e. H. . Bayes' rule for linear discriminant analysis (LDA) then reads ${\displaystyle i}$ ${\displaystyle \pi _{i}}$ ${\displaystyle K}$ ${\displaystyle X}$ ${\displaystyle i}$ ${\displaystyle \mu _{i}}$ ${\displaystyle \Sigma }$ ${\displaystyle X\sim N(\mu _{i},\Sigma )}$

${\displaystyle \delta ^{*}(x)=arg\min _{j\in \{1,...,K\}}\sum _{i=1,i\neq j}^{K}[\log(c_{j|i})+\log(\pi _{i})+x^{T}\Sigma ^{-1}\mu _{i}-{\frac {1}{2}}\mu _{i}^{T}\Sigma ^{-1}\mu _{i}],}$

where denotes the costs that arise when an object belonging to group i is mistakenly assigned to group j. ${\displaystyle c_{j|i}}$

In the above model, if one does not assume that the covariance matrices in the groups are identical, but that they can differ, i.e. H. , this is Bayes' rule for quadratic discriminant analysis (QDA) ${\displaystyle X\sim N(\mu _{i},\Sigma _{i})}$

${\displaystyle \delta ^{*}(x)=arg\min _{j\in \{1,...,K\}}\sum _{i=1,i\neq j}^{K}[\log(c_{j|i})+\log(\pi _{i})-{\frac {1}{2}}\log |\Sigma _{i}|-{\frac {1}{2}}(x-\mu _{i})^{T}\Sigma _{i}^{-1}(x-\mu _{i})].}$

The limits when performing the linear discriminant analysis are linear in , with the quadratic quadratic. ${\displaystyle x}$

See also: Bayesian classifier

Classification in the case of unknown distribution parameters

Most of the time, the distributions of the underlying characteristics will be unknown. So you need to be appreciated. A so-called learning sample is taken from both groups to the extent or . With this information, the expected value vectors and the covariance matrix estimated . As in the case above, the Mahalanobis distance or the discriminant function is used, with the estimated instead of the true parameters. ${\displaystyle n_{I}}$ ${\displaystyle n_{II}}$ ${\displaystyle \mu _{i}(i=I,II)}$ ${\displaystyle \Sigma _{i}}$

Assuming the standard model with group-like covariance matrices, the equality of the covariance matrices must first be confirmed with the help of Box's M test .

example

Amusement park example from above:

The population is now unknown. 16 families in each group were examined more closely. The following values ​​resulted in the sample:

Family expenses at an amusement park
Group 1			Group 2
total	Souvenirs	group	total	Souvenirs	group
64.78	37.08	1	54.78	17.08	2
67.12	38.44	1	57.12	18.44	2
71.58	44.08	1	61.58	24.08	2
63.66	37.40	1	53.66	17.40	2
53.80	19.00	1	43.80	7.99	2
73.21	41.17	1	63.21	29.10	2
63.95	31.40	1	53.95	11.40	2
78.33	45.92	1	68.33	34.98	2
72.36	38.09	1	62.36	18.09	2
64.51	34.10	1	54.51	14.10	2
66.11	34.97	1	56.11	14.97	2
66.97	36.90	1	56.97	16.90	2
69.72	41.24	1	59.72	21.24	2
64.47	33.81	1	54.47	13.81	2
72.60	19.05	1	62.60	30.02	2
72.69	39.88	1	62.69	19.88	2

The means for each group, the overall mean, the covariance matrices, and the pooled (pooled) covariance were calculated as follows:

variable	Pooled Mean	Means for
		Group 1	Group 2
total	62.867	67.867	57.867
souvenir	27,562	35.783	19,342

Pooled Covariance Matrix
	total	souvenir
total	32.59
souvenir	30.58	54.01

Covariance Matrix for Group 1
	total	souvenir
total	32.59
souvenir	25.34	56.90

Covariance Matrix for Group 2
	total	souvenir
total	32.59
souvenir	35.82	51.11

The discriminant function is obtained from this using the above formula

${\displaystyle f(x)=-4{,}690+0{,}020\cdot {\text{Gesamt}}+0{,}124\cdot {\text{Souvenir}}}$.

The classification rule is now:

Assign the object to group I if

${\displaystyle f(x)>0}$

is.

The sample values ​​can be classified in order to check the quality of the model. The classification matrix results here

group	Correctly assigned	incorrectly assigned
I.	14th	2
II	13	3

Now the family with the observations should be arranged again. ${\displaystyle (65;35)}$

The following graphic shows the scatter plot of the learning sample with the group means. The green point is the location of the object . ${\displaystyle (65;35)}$

The graphic already shows that this object belongs to group I. The discriminant function gives

${\displaystyle f(x)=-4{,}690+0{,}020\cdot 65+0{,}124\cdot 35=0{,}967.}$

There

${\displaystyle f(x)>0}$

the object is assigned to group I.

More keywords

• Wilks Lambda
• Flexible discriminant analysis
• Kernel density estimator
• Support vector machine

literature

• Maurice M. Tatsuoka: Multivariate Analysis: Techniques for Educational and psychological Research. John Wiley & Sons, Inc., New York, 1971, ISBN 0-471-84590-6
• KV Mardia, JT Kent, JM Bibby: Multivariate Analysis . New York, 1979
• Ludwig Fahrmeir, Alfred Hamerle, Gerhard Tutz (ed.): Multivariate statistical methods . New York, 1996
• Joachim Hartung , Bärbel Elpelt: Multivariate Statistics . Munich, Vienna, 1999
• Backhaus, Klaus; Erichson, Bernd; Plinke, Wulff et al. a .: Multivariate analysis methods.

Web links

• Springer Encyclopaedia of Mathematics: Discriminant analysis (English)

Individual evidence

1. ↑ Klaus Backhaus, SpringerLink (Online service): Multivariate Analysis Methods an application-oriented introduction . Springer, Berlin 2006, ISBN 978-3-540-29932-5 .
2. ^ RA Fisher (1936), The use of multiple measurements in taxonomic problems , Annals Eugen., Vol. 7, pp. 179-188, doi : 10.1111 / j.1469-1809.1936.tb02137.x