Support vector machine
A support vector machine [ səˈpɔːt ˈvektə məˈʃiːn ] ( SVM , the translation from English , “ support vector machine ” or support vector method is not in use) serves as a classifier (see classification ) and a regressor (see regression analysis ). A support vector machine divides a number of objects into classes in such a way that the widest possible area around the class boundaries remains free of objects; it is a so-called Large Margin Classifier (Eng. "broad margin classifier").
Support vector machines are not machines in the conventional sense, i.e. they do not consist of tangible components. It is a purely mathematical method of pattern recognition that is implemented in computer programs. Accordingly, the part of the name machine does not refer to a machine , but to the area of origin of the support vector machines, machine learning .
Basic functionality
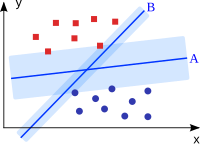
The starting point for building a support vector machine is a set of training objects, for which it is known which class they belong to. Each object is represented by a vector in a vector space . The task of the support vector machine is to fit a hyperplane into this space , which acts as a separating surface and divides the training objects into two classes. The distance between those vectors that are closest to the hyperplane is maximized. This wide, empty border should later ensure that objects that do not exactly correspond to the training objects are classified as reliably as possible.
When using the hyperplane, it is not necessary to consider all training vectors. Vectors that are further away from the hyperplane and are, so to speak, "hidden" behind a front of other vectors do not affect the location and position of the parting plane. The hyperplane only depends on the vectors closest to it - and only these are needed to describe the plane mathematically exactly. These vectors are closest to their function support vectors (Engl. Support vectors ) called and helped to support vector machines to their name.
A hyperplane cannot be "bent", so that a clean separation with a hyperplane is only possible if the objects can be separated linearly . This condition is generally not met for real training object sets. In the case of non-linearly separable data, support vector machines use the kernel trick to draw in a non-linear class boundary.
The idea behind the kernel trick is to transfer the vector space and thus also the training vectors in it to a higher-dimensional space. In a space with a sufficiently high number of dimensions - in case of doubt, infinite - even the most nested set of vectors can be linearly separated. In this higher-dimensional space, the separating hyperplane is now determined. During the reverse transformation into the lower-dimensional space, the linear hyperplane becomes a non-linear, possibly even non-contiguous hypersurface , which neatly separates the training vectors into two classes.
There are two problems with this process: The high transformation is extremely computationally heavy and the representation of the interface in the low-dimensional space is generally incredibly complex and therefore practically unusable. This is where the kernel trick comes in. If one uses suitable kernel functions to describe the interface, which describe the hyperplane in the high-dimensional and still remain “benign” in the low-dimensional, it is possible to implement the forward and reverse transformation without actually having to perform it arithmetically. Here, too, some of the vectors are sufficient, namely again the support vectors, in order to fully describe the class boundary.
Both linear and non-linear support vector machines can be designed more flexibly with additional slip variables . The slip variables allow the classifier to incorrectly classify individual objects, but at the same time “punish” any such misclassification. In this way, on the one hand, overfitting is avoided and, on the other hand, the required number of support vectors is reduced.
Mathematical implementation
The SVM determines based on a set of training examples
a hyperplane that separates the two classes as clearly as possible.
This clearly means the following: A normal vector describes a straight line through the coordinate origin. Hyperplanes run perpendicular to this straight line. Each intersects the line at a certain distance from the origin (as measured in the opposite direction to ). This distance is called a bias . Together, the normal vector and the bias clearly define a hyperplane, and the following applies to the points belonging to it :
- .
For points that are not on the hyperplane, the value is not zero, but positive (on the side that is pointing) or negative (on the other side). The sign can be used to name the side on which the point lies.
If the hyperplane separates the two classes, then the sign is positive for all points in one class and negative for all points in the other class. The aim now is to find such a hyperplane.
If one expresses the class membership in the training examples , then this results in a formulaic condition
If such a hyperplane exists at all, then there are infinitely many that differ only minimally and are sometimes very close to one or the other class. But then there is the risk that data points that will be encountered in the future will be on the “wrong” side of the hyperplane and thus be interpreted incorrectly.
The hyperplane should therefore be such that the smallest distance of the training points onto the hyperplane, the so-called margin (from English margin , margin), is maximized to ensure the best possible generalization to the classifier.
The aim of so-called training is to calculate the parameters and this “best” hyperplane.
The hyperplane is then used as a decision function. This means: it is assumed that the calculated sign will also correctly reflect the class membership for future data points. In particular, a computer can easily and automatically carry out the classification by simply calculating the sign.
Linear separable data
Many learning algorithms work with a linear function in the form of a hyperplane. Are two classes of examples separable from one another by a hyperplane, i.e. H. linearly separable , however, there are usually an infinite number of hyperplanes that separate the two classes from each other. The SVM differs from other learning algorithms in that it selects the one with the minimum quadratic norm from all possible separating hyperplanes , so that the same applies for every training example . This is equivalent to maximizing the smallest distance to the hyperplane (the margin ). According to the statistical learning theory , the complexity of the class of all hyperplanes with a certain margin is lower than that of the class of all hyperplanes with a smaller margin. From this, upper bounds for the expected generalization error of the SVM can be derived.
The optimization problem can then be written as:
- Minimize the term by adjusting the variables ,
- so that the constraint applies to everyone .
Non-linearly separable data
As a rule, the training examples cannot be strictly linearly separated. This can u. a. measurement errors in the data, or the fact that the distributions of the two classes naturally overlap. In this case, the optimization problem is changed in such a way that violations of the secondary conditions are possible, but the violations should be kept as small as possible. For this purpose, a positive slip variable is introduced for each secondary condition, the value of which is the violation of the secondary conditions. means that the secondary condition is violated. Since the sum of the violations should be kept as small as possible, the sum of the errors is added to the target function and thus also minimized. In addition, this sum is multiplied by a positive constant that regulates the balance between the minimization of and the correct classification of the training examples. The optimization problem then has the following form:
- Minimize the term by adjusting the variables ,
- so that the constraint applies to everyone .
Dual problem
Both optimization criteria are convex and can be efficiently solved with modern methods. This simple optimization and the property that support vector machines largely avoid over-fitting to the test data used to design the classifier have made the method extremely popular and widely used.
The optimization problem described above is usually solved in its dual form. This formulation is equivalent to the primal problem in the sense that all solutions to the dual are also solutions to the primal problem. The conversion results from the fact that the normal vector can be written as a linear combination of training examples:
The dual form is derived with the help of the Lagrange multipliers and the Karush-Kuhn-Tucker conditions . It is:
- maximize for : ,
- so that the constraints and apply.
The classification rule thus results:
The SVM got its name from a special subset of the training points, which are Lagrangian variables . These are called support vectors and are either on the margin (if ) or within the margin ( ).
Nonlinear extension with kernel functions
The algorithm described above classifies the data using a linear function. However, this is only optimal if the underlying classification problem is also linear. In many applications this is not the case. One possible way out is to map the data in a space of higher dimensions.
The following applies . This mapping increases the number of possible linear separations (Cover's theorem). SVMs are characterized by the fact that this extension can be integrated very elegantly. In the optimization problem on which the algorithm is based in the formulation presented last, the data points are only included in scalar products. It is therefore possible to replace the inner product in the input space with an inner product in and to calculate it directly instead. The cost of this calculation can be greatly reduced if a positively defined kernel function is used instead:
By this method, a hyperplane (i.e., a linear function) in a high-dimensional space can be calculated implicitly. The resulting classifier has the form
with . By using kernel functions , SVMs can also operate on general structures such as graphs or strings and are therefore very versatile. Although a possibly infinite-dimensional space is implicitly used by the mapping , SVM still generalize very well. It can be shown that the expected test error for maximum margin classifiers is limited and does not depend on the dimensionality of the space.
history
Ronald A. Fisher had the idea of separation by a hyperplane as early as 1936 . It was taken up again in 1958 by Frank Rosenblatt in his contribution to the theory of artificial neural networks . The idea of the support vector machines goes back to the work of Wladimir Wapnik and Alexei Jakowlewitsch Chervonenkis . At the theoretical level, the algorithm is motivated by the principle of structural risk minimization, which states that not only the training error but also the complexity of the model used determine the generalization ability of a classifier. SVMs had their breakthrough in the mid-1990s, and numerous advancements and modifications have been published in recent years.
software
Libraries for SVMs
- libsvm , implemented in C ++ and ported to Java
- liblinear , implemented in C ++ and ported to Java
- SVMlight , based on C
Machine learning and data mining software that contain SVMs
- GNU Octave uses SVMlight
- KNIME
- Matlab uses libsvm , SVMlight and Spider
- RapidMiner uses libsvm and an SVM implemented in Java
- Scikit-learn uses libsvm and liblinear .
- Shogun uses libsvm and SVMlight
- WEKA uses libsvm and Spider
SVM modules for programming languages (selection)
- Perl has modules for libsvm and SVMlight
- R , has packages based on libsvm (package e1071 ), SVMlight (package klaR ) and has the package kernlab for kernel learning with SVMs
- Ruby has modules for libsvm and SVMlight
literature
- Bernhard Schölkopf , Alex Smola: Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond (Adaptive Computation and Machine Learning) , MIT Press, Cambridge, MA, 2002, ISBN 0-262-19475-9 .
- Ingo Steinwart , Andreas Christmann: Support Vector Machines , Springer, New York, 2008. ISBN 978-0-387-77241-7 . 602 pp.
- Nello Cristianini, John Shawe-Taylor: Kernel Methods for Pattern Analysis , Cambridge University Press, Cambridge, 2004, ISBN 0-521-81397-2
- Christopher JC Burges: A Tutorial on Support Vector Machines for Pattern Recognition , Data Mining and Knowledge Discovery, 2 (2): 121-167, 1998.
- Vladimir Vapnik : Statistical Learning Theory , Wiley, Chichester, GB, 1998.
- Vladimir Vapnik: The Nature of Statistical Learning Theory , Springer Verlag, New York, NY, USA, 1995.
Individual evidence
- ↑ Schölkopf, Smola: Learning with Kernels, MIT Press, 2001
- ↑ Fisher, RA (1936), “The use of multiple measurements in taxonomic problems”, in Annals of Eugenics 7 : 179-188, doi : 10.1111 / j.1469-1809.1936.tb02137.x
- ↑ Rosenblatt, F. (1958), "The Perceptron, a Probabilistic Model for Information Storage and Organization in the Brain", in Psychological Review, 62/386, pp. 386-408, doi : 10.1037 / h0042519 .
- ↑ Vapnik and Chervonenkis, Theory of Pattern Recognition, 1974 (German translation: Wapnik and Tschervonenkis, Theory of Pattern Recognition, 1979)
- ^ David Meyer et al .: R-Paket e1071. Misc Functions of the Department of Statistics, Probability Theory Group (Formerly: E1071), TU Wien. In: CRAN. The R Foundation, accessed on May 14, 2016 (English, current version: 1.6-7).
- ↑ Uwe Ligges et al .: R-Paket klaR. Classification and visualization. In: CRAN. The R Foundation, accessed on May 14, 2016 (English, current version: 0.6-12).
- ↑ Alexandros Karatzoglou, Alex Smola, Kurt Hornik: R-Paket kernlab. Kernel-Based Machine Learning Lab. In: CRAN. The R Foundation, accessed on May 14, 2016 (English, current version: 0.9-24).