Gauge integral

The gauge integral (also: Eichintegral , Henstock-Integral , Henstock-Kurzweil-Integral ) is an integral type of descriptive nature, the current formulation of which was only discovered in the middle of the 20th century by the mathematician Jaroslav Kurzweil . Ralph Henstock devoted himself to developing the theory of this type of integral. A central estimate, the so-called Henstock Lemma, is named after him. The precursor is the (equivalent) Denjoy-Perron integral, which, however, is based on a very technical and non-illustrative definition.

The specialty of the gauge integral is that every derivation function can be automatically (i.e. without additional requirements) integrable with . In addition, there are conditionally integrable functions in the theory of the gauge integral . These are functions that can be integrated, but not their amount. In both the Riemann and Lebesgue definitions, the integrability of a function always means that its amount can be integrated. ${\displaystyle f'\colon {[a,b]}\rightarrow \mathbb {R} }$ ${\displaystyle \textstyle \int _{a}^{b}f'(t)\mathrm {d} t=f(b)-f(a)}$

The gauge integral contains both the Riemann and Lebesgue integrals as special cases; That is, every Riemann or Lebesgue integrable function is Gauge integrable; However, since there are functions that are neither Riemann- nor Lebesgue-integrable, but still gauge-integrable, the gauge integral represents a real extension of the Lebesgue integral.

The integral owes the name “gauge” to its definition: Similar to the Riemann integral, decompositions and Riemann sums are used for the calibration integral, but the fineness of a decomposition is given a special interval value Function, called calibration function , assessed.

introduction

The main sentence

The main theorem of differential and integral calculus (its 1st part in common counting) is a central proposition in the theory of the Riemann and Lebesgue integral . It reads:

• Set: If a derivative function of over the interval , then applies integrable Riemann (or Lebesgue) . ${\displaystyle f'}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle \int _{a}^{b}f'(t)\mathrm {d} t=f(b)-f(a)}$

In practice, the main theorem provides one of the most important methods of determining the value of an integral concretely and precisely. For example, if you want to integrate the function with over , then you understand f as the derivative function of a function , called an antiderivative . Obviously is given by an antiderivative of such that it follows: ${\displaystyle f\colon [0,1]\rightarrow \mathbb {R} }$ ${\displaystyle f(x)=x^{2}}$ ${\displaystyle [0,1]}$ ${\displaystyle F\colon [0,1]\rightarrow \mathbb {R} }$ ${\displaystyle F(x)={\tfrac {1}{3}}x^{3}}$ ${\displaystyle f}$

${\displaystyle \int _{0}^{1}x^{2}=F(1)-F(0)={\frac {1}{3}}1^{3}-{\frac {1}{3}}0^{3}={\frac {1}{3}}}$

For both the Riemann and Lebesgue integral, however, the integrability of must be stated as a prerequisite - not every derivative function is necessarily integrable. Rather, it shows that there are derivative functions that are neither Riemann nor Lebesgue integrable. One example is the function with ${\displaystyle f'}$ ${\displaystyle g\colon [0,1]\rightarrow \mathbb {R} }$

Figure 1: Representation of the function g and its derivative (the function g was scaled with a factor of 150)

${\displaystyle g(x)={\begin{cases}x^{2}\cos \left({\frac {\pi }{x^{2}}}\right)&{\text{ für }}x>0\\0&{\text{ für }}x=0\end{cases}}}$

(see Fig. 1). Your derivation is through

${\displaystyle g'(x)={\begin{cases}2x\cos \left({\frac {\pi }{x^{2}}}\right)+{\frac {2\pi }{x}}\sin \left({\frac {\pi }{x^{2}}}\right)&{\text{ für }}x>0\\0&{\text{ für }}x=0\end{cases}}}$

given. Since there is no restriction , Riemann cannot be integrated either. One can show that Lebesgue cannot be integrated either. ${\displaystyle g'}$ ${\displaystyle g'}$ ${\displaystyle g'}$

A (descriptive) analysis of the reasons why Riemann is not integrable leads to a decisive improvement in the Riemann definition. To do this, you first think about where the formula comes from. ${\displaystyle g'}$ ${\displaystyle \textstyle \int _{a}^{b}f'(t)\mathrm {d} t=f(b)-f(a)}$

The straddle lemma and the problems of the Riemann integral

After the mean value theorem of differential calculus there is a differentiable function on an interval a with ${\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }$ ${\displaystyle [x,y]\subset [a,b]}$ ${\displaystyle c\in [x,y]}$

${\displaystyle f'(c)={\frac {f(y)-f(x)}{y-x}}.}$

If you choose intermediate points for a decomposition according to the mean value theorem , the result for Riemann sums is : ${\displaystyle Z=\{x_{0},\dots ,x_{n}\}}$ ${\displaystyle c_{i}\in [x_{i-1},x_{i}]}$ ${\displaystyle S(f',Z,c_{1},\dots ,c_{n})}$

${\displaystyle {\begin{array}{rcl}S(f',Z,c_{1},\dots ,c_{n})&=&\sum _{i=1}^{n}f'(c_{i})(x_{i}-x_{i-1})=\sum _{i=1}^{n}{\frac {f(x_{i})-f(x_{i-1})}{x_{i}-x_{i-1}}}(x_{i}-x_{i-1})\\&=&\sum _{i=1}^{n}(f(x_{i})-f(x_{i-1}))=f(b)-f(a)\end{array}}}$

Figure 2: The tangent at the point at the point and the secant above the interval in which lies are almost parallel, the secant slope (mean slope above ) is a good approximation of the tangent slope (punctual slope). ${\displaystyle t}$ ${\displaystyle [x,y]}$ ${\displaystyle t}$ ${\displaystyle [x,y]}$

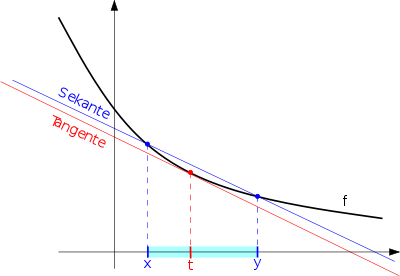
The last sum represented a telescope sum . For other intermediate points i applies in the above calculation. A. no equality, but for the proof of it is not necessary that all Riemann sums are exactly the same . It is sufficient for the Riemann sums to approximate the number for any intermediate places as long as one chooses the decomposition under consideration with sufficient precision. This would be the case, for example, if a function on each interval for all the approximation ${\displaystyle \int _{a}^{b}f'(t)\mathrm {d} t=f(b)-f(a)}$ ${\displaystyle f(b)-f(a)}$ ${\displaystyle f(b)-f(a)}$ ${\displaystyle f}$ ${\displaystyle [x,y]\subset [a,b]}$ ${\displaystyle t\in [x,y]}$

${\displaystyle (1)\ \ \ {\frac {f(y)-f(x)}{y-x}}\approx f'(t)}$

is fulfilled, whereby the error resulting from the approximation becomes arbitrarily small, as long as the interval is only sufficiently small (Fig. 2). ${\displaystyle [x,y]}$

But there are functions that do not show this behavior. One such function is the function from the previous section. Consider, for example, the interval for any (even arbitrarily small) : oscillates "wildly back and forth" near 0, therefore a position can be found on every interval of this form (no matter how small it is) , so that an arbitrarily large positive or is negative number. The average slope over the interval, however, tends towards 0 when it tends towards 0. Finally, and the average slope of g over the interval is just the difference quotient of at 0: ${\displaystyle g}$ ${\displaystyle [0,x_{1}]}$ ${\displaystyle 0<x_{1}<1}$ ${\displaystyle g'}$ ${\displaystyle t_{1}}$ ${\displaystyle g'(t_{1})}$ ${\displaystyle x_{1}}$ ${\displaystyle g'(0)=0}$ ${\displaystyle [0,x_{1}]}$ ${\displaystyle g}$

${\displaystyle (*)\ \ \ {\frac {g(x_{1})-g(0)}{x_{1}-0}}\approx g'(0)=0{\text{ für kleine }}x_{1}}$

${\displaystyle g'(t_{1})}$can therefore deviate as much as you want from the average gradient on the interval . Since every decomposition Z “contains” an interval of this form, there is a subinterval and certain intermediate points for each decomposition for which the approximation is violated. As in the case of the function g, this can lead to a situation where Riemann is not integrable, because according to the Riemann definition, all intermediate points for a decomposition Z must be examined. It would be desirable to have an integral definition in which only certain intermediate points need to be considered at certain sub-intervals. For the purpose of integrating the function it would be e.g. For example, it is helpful to only allow the intermediate point 0 for the sub-interval , because according to this approximation would be  fulfilled. ${\displaystyle [0,x_{1}]}$ ${\displaystyle (1)}$ ${\displaystyle g'}$ ${\displaystyle g'}$ ${\displaystyle [0,x_{1}]}$ ${\displaystyle (*)}$ ${\displaystyle (1)}$

An integration theory that is based on Riemann sums and in which every derivative function is integrable should, according to the previous considerations, only consider pairs of decompositions and intermediate points for which ${\displaystyle Z=\{x_{0},\dots ,x_{n}\}}$ ${\displaystyle t_{1},\dots ,t_{n}}$

${\displaystyle (2)\ \ \ f'(t_{i})\approx {\frac {f(x_{i})-f(x_{i-1})}{x_{i}-x_{i-1}}}}$

applies. The following sentence opens up a way of identifying such pairs:

• Theorem (Straddle Lemma): Let be differentiable in . Then there is a with for everyone with and . ${\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }$ ${\displaystyle t\in [a,b]}$ ${\displaystyle \epsilon >0}$ ${\displaystyle \delta (t)>0}$ ${\displaystyle |f(y)-f(x)-f'(t)(y-x)|\leq \epsilon (y-x)}$ ${\displaystyle x,y\in [a,b]}$ ${\displaystyle x\leq t\leq y}$ ${\displaystyle [x,y]\subset (t-\delta (t),t+\delta (t))}$

If the inequality of the straddle-lemma by dividing its core message is revealed: At any point there is a closed interval , for the ${\displaystyle y-x}$ ${\displaystyle t\in [a,b]}$ ${\displaystyle [x,y]\subset [a,b]}$

${\displaystyle f'(t)\approx {\frac {f(y)-f(x)}{y-x}}}$

applies. The number indicates the error of this approximation. Since it can be arbitrary, in particular arbitrarily small, an interval can even always be found on which the above approximation is arbitrarily good. The only requirement is that the interval limits and are sufficiently close to , or to put it another way: The requirement is that the interval is in a sufficiently small area of : ${\displaystyle \epsilon >0}$ ${\displaystyle \epsilon }$ ${\displaystyle [x,y]}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle t}$ ${\displaystyle [x,y]}$ ${\displaystyle t}$

${\displaystyle [x,y]\subset (t-\delta (t),t+\delta (t))}$

If one now selects only those pairs from the decomposition together with intermediate points for which the condition ${\displaystyle Z=\{x_{0},\dots ,x_{n}\}}$ ${\displaystyle t_{1},\dots ,t_{n}}$

${\displaystyle (3)\ [x_{i-1},x_{i}]\subset (t_{i}-\delta (t_{i}),t_{i}+\delta (t_{i}))}$

applies (where the choice is made according to the straddle lemma), then the approximation is always fulfilled, and all associated Riemann sums are close to , as desired. ${\displaystyle \delta }$ ${\displaystyle (2)}$ ${\displaystyle f(b)-f(a)}$

Figure 3: Riemann's definition of refinement is not sufficient to assess whether a decomposition and associated intermediate points satisfy the condition . The splits and are equally fine in the sense of Riemann (the largest sub-interval is always the same length). For the intermediate point , the condition for the decomposition is fulfilled, but not for despite the same fineness. ${\displaystyle (3)}$ ${\displaystyle Z_{1}}$ ${\displaystyle Z_{2}}$ ${\displaystyle t}$ ${\displaystyle (3)}$ ${\displaystyle Z_{1}}$ ${\displaystyle Z_{2}}$

The question now arises as to how one selects such “suitable” combinations from all possible combinations of intermediate points and splits. The Riemann definition of fineness, i.e. H. looking at the largest interval length , is not fit to do so. Obviously, the selected intermediate points and thus the positions of the sub-intervals are not included in the evaluation of the fineness of the decomposition . However, the relevant number from the straddle lemma is i. A. depend on the location ! One will z. B. expect that the smaller it is, the stronger it oscillates near this point. It can therefore happen that the condition is fulfilled for a breakdown and intermediate points , but not for an equally fine breakdown (see Figure 3) - not even if the same intermediate point is considered. The aim will therefore be to create an improved definition of fineness that takes the position of the partial intervals into account. ${\displaystyle \mu (Z)=\max\{x_{i}-x_{i-1}:i=1,\dots ,n\}}$ ${\displaystyle [x_{i-1},x_{i}]}$ ${\displaystyle Z}$ ${\displaystyle \delta (t)>0}$ ${\displaystyle t}$ ${\displaystyle \delta (t)}$ ${\displaystyle f}$ ${\displaystyle Z_{1}}$ ${\displaystyle t_{1},\dots ,t_{n}}$ ${\displaystyle (3)}$ ${\displaystyle Z_{2}}$ ${\displaystyle [x_{i-1},x_{i}]}$

Basic ideas

In summary, the "guidelines" for the definition of the gauge integral are:

• As part of a new integral type, it should be possible to automatically integrate every derivation function (i.e. without additional requirements) with . ${\displaystyle f'}$ ${\displaystyle \int _{a}^{b}f'(t)\mathrm {d} t=f(b)-f(a)}$
• To this end, the relationship between intermediate points and splits must be re-regulated so that it is possible to combine intermediate points with splits that “fit together well”. To do this, a fine term must be created that
  • the positions of the sub-intervals , , taken into account and ${\displaystyle [x_{i-1},x_{i}]}$ ${\displaystyle i=1,\dots ,n}$
  • which allows only certain intermediate points to be permitted at certain sub-intervals.

The formal definition

Preliminary work

Since only “matching” decompositions and intermediate points are to be considered for the new integral, it makes sense to first combine the two terms in one term.

• Definition (highlighted decomposition) . Let be a decomposition of an interval and intermediate points belonging to Z, i.e. i.e. it applies to . The amount is called a marked decomposition (engl .: tagged partition) of the interval . ${\displaystyle Z=\{x_{0},\dots ,x_{n}\}}$ ${\displaystyle [a,b]}$ ${\displaystyle t_{1},\dots ,t_{n}}$ ${\displaystyle t_{i}\in [x_{i-1},x_{i}]}$ ${\displaystyle i=1,\dots ,n}$ ${\displaystyle D=\{(t_{i},[x_{i-1},x_{i}]):i=1,\dots ,n\}=:\{(t_{i},I_{i}):i=1,\dots ,n\}}$ ${\displaystyle [a,b]}$

A marked decomposition thus contains ordered pairs of the form , with a closed interval and a number with . Riemann sums with regard to a function and a marked decomposition are defined exactly like Riemann's subtotals by: ${\displaystyle (t,I)}$ ${\displaystyle I}$ ${\displaystyle t}$ ${\displaystyle t\in I}$ ${\displaystyle S(f,D)}$ ${\displaystyle f}$ ${\displaystyle D}$

${\displaystyle S(f,D):=\sum _{i=1}^{n}f(t_{i})l(I_{i})=\sum _{i=1}^{n}f(t_{i})(x_{i}-x_{i-1})}$

The following definition lays the groundwork for an improved definition of fineness:

• Definition (calibration function): An interval-valued function on the interval is called a calibration function if and is an open interval. ${\displaystyle \gamma }$ ${\displaystyle [a,b]}$ ${\displaystyle t\in \gamma (t)}$ ${\displaystyle \gamma (t)}$

Figure 4: Above: A calibration function assigns an open interval (green) to each point . Below: A highlighted decomposition is -fine, if for . ${\displaystyle x\in [a,b]}$ ${\displaystyle \gamma (x)}$ ${\displaystyle D=\{(t_{i},[x_{i-1},x_{i}]):i=1,\dots ,n\}}$ ${\displaystyle \gamma }$ ${\displaystyle [x_{i-1},x_{i}]\subset \gamma (t_{i})}$ ${\displaystyle i=1,\dots ,n}$

A calibration function assigns an open interval that contains to each point . The term calibration function can now be used to define a very flexible degree of fineness that not only takes into account the position of the sub-intervals of a decomposition , but also regulates the relationship between the decomposition and intermediate points: A marked decomposition should then be called -fine if one Is the calibration function and each sub- interval lies within the open interval that delivers at the intermediate point belonging to the sub-interval : ${\displaystyle t\in [a,b]}$ ${\displaystyle \gamma (t)}$ ${\displaystyle t}$ ${\displaystyle \gamma }$ ${\displaystyle I_{i}=[x_{i-1},x_{i}]}$ ${\displaystyle Z}$ ${\displaystyle D}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle I_{i}=[x_{i-1},x_{i}]}$ ${\displaystyle \gamma }$ ${\displaystyle t_{i}}$

• Definition: Let be a gauge function on the interval [a, b] and a marked decomposition of this interval. means -fine , if for everyone . ${\displaystyle \gamma }$ ${\displaystyle D=\{(t_{i},I_{i}):i=1,\dots ,n\}}$ ${\displaystyle D}$ ${\displaystyle \gamma }$ ${\displaystyle I_{i}\subset \gamma (t_{i})}$ ${\displaystyle i=1,\dots ,n}$

example

By restricting to fine decompositions, it is possible - through a clever choice of the calibration function  - to select only suitable pairs of decompositions and support points. Be about and a decomposition of this interval. If (as in the example of the function ) the only possible intermediate point to the partial interval is to be allowed, it is defined as follows: ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle [a,b]=[0,1]}$ ${\displaystyle Z}$ ${\displaystyle g'}$ ${\displaystyle 0}$ ${\displaystyle I_{1}=[0,x_{1}]}$ ${\displaystyle \gamma }$

${\displaystyle \gamma (t)={\begin{cases}(-\delta (0),\delta (0))&{\text{ für }}t=0\\(t-\delta (t),t+\delta (t))&{\text{ für }}t\neq 0\end{cases}}}$

Be and be arbitrary. Then the only open interval given by that contains the 0. For each marked decomposition of but apply must: . Because of this , a marked decomposition can only be -fine if . The sub-interval occurs in every -fine marked decomposition exclusively together with the intermediate point 0. Furthermore, due to the function's dependency, the smallness of a sub-interval of a marked breakdown can be “set” depending on the intermediate point and thus on the position of the sub-interval. ${\displaystyle 0<\delta (t)<{\frac {t}{2}}}$ ${\displaystyle \delta (0)>0}$ ${\displaystyle \gamma (0)}$ ${\displaystyle \gamma }$ ${\displaystyle D}$ ${\displaystyle [0,1]}$ ${\displaystyle I_{1}\subset \gamma (t_{1})}$ ${\displaystyle 0\in I_{1}}$ ${\displaystyle \gamma }$ ${\displaystyle t_{1}=0}$ ${\displaystyle I_{1}=[0,x_{1}]}$ ${\displaystyle \gamma }$ ${\displaystyle t}$ ${\displaystyle \delta }$ ${\displaystyle I_{i}}$ ${\displaystyle D}$ ${\displaystyle t_{i}}$

Definition of the gauge integral

Figure 5 Approximation of the area between the graph of a function and the axis by means of Riemann subtotals (orange rectangles) ${\displaystyle f}$ ${\displaystyle x}$

The gauge integral is now - similar to the Riemann integral - defined as a fixed number , which Riemann sums with respect to marked decompositions of an interval can approach, provided that these decompositions are selected precisely with respect to suitable calibration functions : ${\displaystyle A}$ ${\displaystyle D=\{(t_{i},I_{i}):i=1,\dots ,n\}}$ ${\displaystyle [a,b]}$ ${\displaystyle \gamma }$

• Definition (gauge integral): A function is called gauge integrable (eichintegrabel, Henstock- (Kurzweil-) integrable) above , if there is a fixed number to each of a calibration function on are such that for each -fine marked decomposition applies. is Gauge Integral (Integral calibration, Henstock- (Kurzweil-) Integral) from over , in symbols . ${\displaystyle f\colon I=[a,b]\rightarrow \mathbb {R} }$ ${\displaystyle [a,b]}$ ${\displaystyle A\in \mathbb {R} }$ ${\displaystyle \epsilon >0}$ ${\displaystyle \gamma }$ ${\displaystyle [a,b]}$ ${\displaystyle |S(f,D)-A|<\epsilon }$ ${\displaystyle \gamma }$ ${\displaystyle D}$ ${\displaystyle A}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle A=\int _{a}^{b}f=\int _{I}f}$

The definition is very reminiscent of the (original) definition of the Riemann integral. The important difference is that the rough Riemann fineness measure (considering the longest sub-interval of the decomposition ) has been replaced by the new, improved measure. Henstock therefore speaks of an "Integral of Riemann-Type" in his work Theories of Integration . ${\displaystyle Z}$

Properties of the gauge integral

As for any other type of integral:

• The value of the gauge integral is clearly determined .

Furthermore, the integral function is linear : ${\displaystyle f\mapsto \int _{a}^{b}f}$

• Are two functions via gauge integrable and , then is gauge integrable over and: . ${\displaystyle f,g}$ ${\displaystyle [a,b]}$ ${\displaystyle \alpha ,\beta \in \mathbb {R} }$ ${\displaystyle \alpha f+\beta g}$ ${\displaystyle [a,b]}$ ${\displaystyle \int _{a}^{b}(\alpha f+\beta g)=\alpha \int _{a}^{b}f+\beta \int _{a}^{b}g}$

The Riemann integral fits easily into the framework of the gauge integral:

• Every Riemann integrable function is also gauge integrable and the two integrals agree.

Let the Riemann integral of over and be chosen in such a way that for each decomposition with and arbitrary intermediate points . If you select the calibration function to ${\displaystyle R\int _{a}^{b}f}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle \delta >0}$ ${\displaystyle \left|R\int _{a}^{b}f-S(f,Z,t_{1},\dots ,t_{n})\right|<\epsilon }$ ${\displaystyle Z}$ ${\displaystyle \mu (Z)<\delta }$ ${\displaystyle t_{1},\dots ,t_{n}}$ ${\displaystyle \gamma }$

${\displaystyle \gamma (t)=\left(t-{\frac {\delta }{2}},t+{\frac {\delta }{2}}\right),}$

then for each -fine marked decomposition by definition: , so . If the decomposition is defined by , then and thus: ${\displaystyle \gamma }$ ${\displaystyle D=\{(t_{i},[x_{i-1},x_{i}]):i=1,\dots ,n\}}$ ${\displaystyle [x_{i-1},x_{i}]\subset \gamma (t_{i})}$ ${\displaystyle x_{i}-x_{i-1}<\delta }$ ${\displaystyle Z}$ ${\displaystyle Z=\{x_{0},\dots ,x_{n}\}}$ ${\displaystyle \mu (Z)<\delta }$

${\displaystyle \left|S(f,D)-R\int _{a}^{b}f\right|=\left|S(f,Z,t_{1},\dots ,t_{n})-R\int _{a}^{b}f\right|<\epsilon }$

The interval additivity known from the Riemann and Lebesgue integral also applies:

• Be and two non-overlapping closed intervals (i. E., The two intervals have at most one point in common edge) and about integrable gauge. Then also gauge integrable and we have: . ${\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }$ ${\displaystyle J_{1},J_{2}\subset [a,b]}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$ ${\displaystyle f}$ ${\displaystyle J_{1},J_{2},J_{1}\cup J_{2}}$ ${\displaystyle \int _{J_{1}\cup J_{2}}f=\int _{J_{1}}f+\int _{J_{2}}f}$

Conversely one finds:

• Be gauge integrable over the non-overlapping intervals . Is , so is also integrable and the following applies: ${\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }$ ${\displaystyle J_{1},\dots ,J_{m}}$ ${\displaystyle [a,b]=\cup _{j=1}^{m}J_{j}}$ ${\displaystyle f}$ ${\displaystyle [a,b]}$

${\displaystyle \int _{a}^{b}f=\sum _{j=1}^{m}\int _{J_{i}}f=\int _{J_{1}}f+\dots +\int _{J_{m}}f}$

The gauge integral is monotonic:

• If gauge-integrable over and (i.e. ), then: ${\displaystyle f,g}$ ${\displaystyle [a,b]}$ ${\displaystyle f\geq g}$ ${\displaystyle f(x)\geq g(x)\,\forall x\in [a,b]}$

${\displaystyle \int _{a}^{b}f\geq \int _{a}^{b}g}$

In particular , if . ${\displaystyle \int _{a}^{b}f\geq 0}$ ${\displaystyle f\geq 0}$

It is particularly interesting that every derivative function is gauge-integrable:

• (Main clause, part 1). Be differentiable. Then over gauge integrable with . ${\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }$ ${\displaystyle f'}$ ${\displaystyle [a,b]}$ ${\displaystyle \int _{a}^{b}f'=f(b)-f(a)}$

The result is obtained after a few skillful transformations by choosing the (symmetrical) calibration function , whereby the straddle lemma is used. Then you evaluate the expression for any -fine marked decomposition . The 2nd part of the main clause reads for the gauge integral: ${\displaystyle \epsilon >0}$ ${\displaystyle \gamma (t)=(t-\delta (t),t+\delta (t))}$ ${\displaystyle \delta (t)}$ ${\displaystyle \gamma }$ ${\displaystyle |S(f,D)-(f(b)-f(a))|}$

• (Main clause, part 2). Be gauge-integrable over . Then the function with is differentiable with almost everywhere in [a, b] . ${\displaystyle f\colon [a,b]\rightarrow \mathbb {R} }$ ${\displaystyle [a,b]}$ ${\displaystyle F\colon [a,b]\rightarrow \mathbb {R} }$ ${\displaystyle F(x)=\int _{a}^{x}f}$ ${\displaystyle F'(x)=f(x)}$

For the indefinite integral of a gauge-integrable function, the statement “ is not differentiable or it is true ” is only correct on a Lebesgue null set . It is important that only the integrability of has to be assumed. Is even continuous, so is everywhere in differentiable with . ${\displaystyle F}$ ${\displaystyle f}$ ${\displaystyle F}$ ${\displaystyle F'(x)\neq f(x)}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle F}$ ${\displaystyle [a,b]}$ ${\displaystyle F'(x)=f(x)}$

The two central convergence theorems known from the Lebesgue integral apply to the gauge integral . These describe the circumstances under which the limit function of a function sequence of gauge-integrable functions is in turn gauge-integrable and integration and limit value formation may be swapped: ${\displaystyle f}$ ${\displaystyle (f_{n})}$

${\displaystyle \lim _{n\rightarrow \infty }\int _{a}^{b}f_{n}=\int _{a}^{b}f=\int _{a}^{b}\lim _{n\rightarrow \infty }f_{n}}$

You get:

Figure 6 : Representation of the first 6 terms of a function sequence that increases monotonically, but does not converge evenly against . The sequence of functions is also restricted equally. ${\displaystyle (f_{n})}$ ${\displaystyle f}$ ${\displaystyle (f_{n})}$

• Theorem about monotonic convergence: Let be an interval, a sequence of functions that are integrable over gauge and . Converges monotonically increasing against , i.e. i.e., holds and for all , then is gauge-integrable over if and only if . In this case: ${\displaystyle I}$ ${\displaystyle (f_{n})}$ ${\displaystyle f_{n}\colon I\rightarrow \mathbb {R} }$ ${\displaystyle I}$ ${\displaystyle f\colon I\rightarrow \mathbb {R} }$ ${\displaystyle (f_{n})}$ ${\displaystyle f}$ ${\displaystyle \lim _{n\rightarrow \infty }f_{n}(x)=f(x)}$ ${\displaystyle f_{n+1}(x)\geq f_{n}(x)}$ ${\displaystyle x\in \mathbb {R} }$ ${\displaystyle f}$ ${\displaystyle I}$ ${\displaystyle \sup \left\{\int _{I}^{\ }f_{n}:n\in \mathbb {N} \right\}<\infty }$

${\displaystyle \int _{I}f=\int _{I}\lim _{n\rightarrow \infty }f_{n}=\lim _{n\rightarrow \infty }\int _{I}f_{n}}$

So if a function sequence converges point by point to a limit function and if the sequence increases monotonically for each and every function is integrable over gauge, then the limit function is integrable over gauge if and only if the sequence is bounded. In this case the integration and the limit value formation can be exchanged, i.e. the two operations can be carried out in reverse order. ${\displaystyle f}$ ${\displaystyle (f_{n}(x))}$ ${\displaystyle x\in I}$ ${\displaystyle f_{n}}$ ${\displaystyle I}$ ${\displaystyle f}$ ${\displaystyle I}$ ${\displaystyle \left(\int _{I}^{\ }f_{n}\right)}$

That also applies

• Theorem about majorized convergence. Let be an interval, a sequence of functions that are integrable over gauge and . Converges pointwise to and there are gauge-integrable functions with almost everywhere in and all , so is over gauge-integrable and the following applies: ${\displaystyle I}$ ${\displaystyle (f_{n})}$ ${\displaystyle f_{n}\colon I\rightarrow \mathbb {R} }$ ${\displaystyle I}$ ${\displaystyle f\colon I\rightarrow \mathbb {R} }$ ${\displaystyle (f_{n})}$ ${\displaystyle f}$ ${\displaystyle \alpha ,\beta \colon I\rightarrow \mathbb {R} }$ ${\displaystyle \alpha \leq f_{n}\leq \beta }$ ${\displaystyle I}$ ${\displaystyle n\in \mathbb {N} }$ ${\displaystyle f}$ ${\displaystyle I}$

${\displaystyle \int _{I}f=\int _{I}\lim _{n\rightarrow \infty }f_{n}=\lim _{n\rightarrow \infty }\int _{I}f_{n}}$

So is there an over gauge integrable minorant and over integrable gauge majorant for , so the limit function is the function sequence gauge integrable over . In this case too, limit value formation and integration can be swapped. ${\displaystyle I}$ ${\displaystyle \alpha }$ ${\displaystyle I}$ ${\displaystyle \beta }$ ${\displaystyle (f_{n})}$ ${\displaystyle f}$ ${\displaystyle (f_{n})}$ ${\displaystyle I}$

Extensions

In the following, the term measurability (and correspondingly related terms) is always to be understood as Lebesgue measurability . So the measure considered is the Lebesgue measure on . ${\displaystyle \mathbb {R} ^{n}}$

Extensions in one dimension

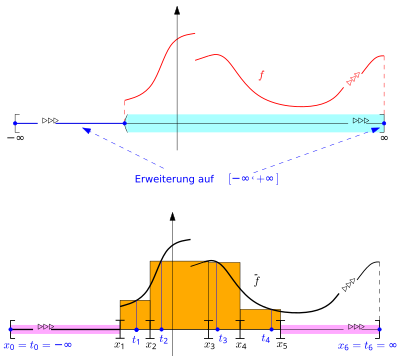
The gauge integral can be extended to infinite intervals. At first glance, this seems surprising. If you look at the interval as an example, you are initially faced with the problem that the interval is not closed. This problem can be solved simply by not taking , but the extended real numbers sets based. One proceeds accordingly when integrating over every open interval : One then always considers the end of the interval in , i.e. the closed interval , whereby and / or are also permitted. But this does not solve the problem: Since the gauge integral works with finite decompositions, in the case of an infinite integration area at least one sub-interval of each marked decomposition is infinitely long (either or or both) and thus the sum ${\displaystyle \mathbb {R} =(-\infty ,\infty )}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle {\overline {\mathbb {R} }}=\mathbb {R} \cup \{-\infty ,+\infty \}=[-\infty ,+\infty ]}$ ${\displaystyle (a,b)}$ ${\displaystyle {\overline {\mathbb {R} }}}$ ${\displaystyle [a,b]}$ ${\displaystyle a=-\infty }$ ${\displaystyle b=\infty }$ ${\displaystyle I=[a,b]}$ ${\displaystyle I}$ ${\displaystyle [x_{0},x_{1}]}$ ${\displaystyle [x_{n-1},x_{n}]}$

${\displaystyle S(f,D)=\sum _{i=1}^{n}f(t_{i})l(I_{i})=\sum _{i=1}^{n}f(t_{i})(x_{i}-x_{i-1})}$

at best infinite, at worst not even defined, provided that two infinitely long intervals occur and f takes values ​​with different signs at the respective intermediate positions (then the undefined expression occurs). One could now define improper integrals similar to the Riemann integral , but it turns out that this is not necessary by using a trick: In the case of an infinite definition interval, one does not examine the integral over , but over , given by: ${\displaystyle \infty -\infty }$ ${\displaystyle I}$ ${\displaystyle f}$ ${\displaystyle {\bar {f}}:[-\infty ,+\infty ]\rightarrow \mathbb {R} }$

${\displaystyle {\bar {f}}(x)={\begin{cases}f(x)&{\text{ für }}x\in I\\0&{\text{ sonst}}\end{cases}}}$

Figure 7 : Above: Representation of an extended function . Bottom: The area between pieces , and the (red background) axis about the two infinitely long intervals omitted if for this or be selected as a repeater. ${\displaystyle {\overline {\mathbb {R} }}}$ ${\displaystyle f}$
${\displaystyle {\bar {f}}}$ ${\displaystyle x}$ ${\displaystyle \infty }$ ${\displaystyle -\infty }$

In particular . The convention should then apply within the Riemann sum. According to this, every Riemann sum is also defined if it contains infinitely long intervals, insofar as these only occur together with the intermediate points . However, this can be enforced by the following definition: ${\displaystyle {\bar {f}}(\infty )={\bar {f}}(-\infty )=0}$ ${\displaystyle S(f,D)}$ ${\displaystyle 0\cdot \infty =0}$ ${\displaystyle S(f,D)}$ ${\displaystyle D}$ ${\displaystyle \pm \infty }$

• Definition: The interval with is called an open interval that contains. Analogous means with an open interval that contains . ${\displaystyle (a,\infty ]}$ ${\displaystyle a\in \mathbb {R} }$ ${\displaystyle \infty }$ ${\displaystyle [-\infty ,b)}$ ${\displaystyle b\in \mathbb {R} }$ ${\displaystyle -\infty }$

It is now possible to define calibration functions in such a way that infinitely long sub-intervals occur exclusively as intermediate points, e.g. B. for the interval : ${\displaystyle \gamma }$ ${\displaystyle \pm \infty }$ ${\displaystyle [-\infty ,\infty ]}$

${\displaystyle \gamma (t)={\begin{cases}[-\infty ,a)&{\text{ für }}t=-\infty \\(t-l(t),t+r(t))&{\text{ für }}t\in \mathbb {R} \\(b,\infty ]&{\text{ für }}t=\infty \end{cases}}}$

Here can be arbitrary real numbers and be any positive real functions. Since and are the only intervals from the range of values that are infinitely long, the sub-interval from a -fine marked decomposition can only occur together with the intermediate point due to the condition . The same applies to the partial interval , which can only occur together with the intermediate point . Using the example of dismantling ${\displaystyle a,b}$ ${\displaystyle r,l}$ ${\displaystyle \gamma (-\infty )}$ ${\displaystyle \gamma (\infty )}$ ${\displaystyle \gamma }$ ${\displaystyle [-\infty ,x_{1}]}$ ${\displaystyle \gamma }$ ${\displaystyle D}$ ${\displaystyle [-\infty ,x_{1}]\subset \gamma (t_{1})}$ ${\displaystyle t_{1}=-\infty }$ ${\displaystyle [x_{n-1},\infty ]}$ ${\displaystyle t_{n}=\infty }$

${\displaystyle D=\{(-\infty ,[-\infty ,1]),(1,[0,1]),(2,[1,3]),(\infty ,[3,\infty ])\}}$

and a function it becomes clear why the problem of infinite / undefined Riemann sums is solved: ${\displaystyle f\colon \mathbb {R} \rightarrow \infty }$

${\displaystyle S({\bar {f}},D)=\underbrace {{\bar {f}}(-\infty )l([-\infty ,1])} _{=0\cdot \infty =0}+f(1)(2-0)+f(2)(3-1)+\underbrace {{\bar {f}}(\infty )l([3,\infty ])} _{=0\cdot \infty =0}=2f(1)+2f(2)}$

The two potentially infinite summands are omitted and the Riemann sum is finite. With these new definitions, the gauge integral can easily be extended to infinite and / or open sub-intervals:

• Definition: Let be any interval and its conclusion in (i.e., it is also allowed and ). 's gauge integrable (Henstock- (Kurzweil-) -integrabel, eichintergrabel) above , if there is a fixed number to each of a calibration function on are such that for each -fine marked decomposition decomposition of . It is called the gauge integral of over , in symbols . ${\displaystyle I\subset \mathbb {R} }$ ${\displaystyle {\bar {I}}=[a,b]}$ ${\displaystyle {\overline {\mathbb {R} }}}$ ${\displaystyle a=-\infty }$ ${\displaystyle b=\infty }$ ${\displaystyle f}$ ${\displaystyle I}$ ${\displaystyle A\in \mathbb {R} }$ ${\displaystyle \epsilon >0}$ ${\displaystyle \gamma }$ ${\displaystyle {\bar {I}}}$ ${\displaystyle |S(f,D)-A|<\epsilon }$ ${\displaystyle \gamma }$ ${\displaystyle D}$ ${\displaystyle {\bar {I}}}$ ${\displaystyle A}$ ${\displaystyle f}$ ${\displaystyle I}$ ${\displaystyle A=\int _{a}^{b}f=\int _{I}f}$

If there is any measurable subset of an interval , it is called gauge-integrable over , if the function over is gauge-integrable. The gauge integral of f is then defined by: ${\displaystyle E\subset I}$ ${\displaystyle I}$ ${\displaystyle f\colon I\rightarrow \mathbb {R} }$ ${\displaystyle E}$ ${\displaystyle f\cdot \chi _{E}}$ ${\displaystyle I}$ ${\displaystyle S(f,D)}$ ${\displaystyle E}$

${\displaystyle \int _{E}^{\ }f:=\int _{I}^{\ }f\chi _{E}}$

If there is a measurable quantity and a measurable function, it is called Gauge-integrable over , if the extension of to , i.e. the function with ${\displaystyle E\subset \mathbb {R} }$ ${\displaystyle f\colon E\rightarrow \mathbb {R} }$ ${\displaystyle f}$ ${\displaystyle E}$ ${\displaystyle f}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle f^{*}\colon \mathbb {R} \rightarrow \mathbb {R} }$

${\displaystyle f^{*}(x)={\begin{cases}f(x)&{\text{ falls }}x\in E\\0&{\text{ sonst }}\end{cases}}}$

is integrable via gauge and one sets ${\displaystyle \mathbb {R} }$

${\displaystyle \int _{E}f:=\int _{\mathbb {R} }f^{*}.}$

It appears:

• If one defines improper gauge integrals similar to the improper integrals in the Riemann theory, then it is improperly gauge-integrable over an infinitely long definition interval if it is actually gauge-integrable in the above sense; moreover, the values ​​of the integrals agree. ${\displaystyle f}$
• All the properties mentioned in the previous section are transferred analogously to the gauge integral extended to infinite definition intervals. The 1st part of the main theorem then applies to every finite sub-interval of an infinitely long integration area , in the 2nd part any fixed point is to be chosen. The content of the sentence then applies to the function , where is possible. ${\displaystyle I}$ ${\displaystyle a\in I}$ ${\displaystyle F(x)=\int _{a}^{x}f}$ ${\displaystyle x<a}$

Due to the interval additivity, all extended definitions coincide with the original definition of the gauge integral over intervals if there is an interval (every interval is measurable). With these definitions the connection to the Lebesgue integral succeeds. It appears: ${\displaystyle E}$

• Be a measurable amount. If Lebesgue is integrable over , then Gauge is also integrable over and the two integrals agree. In particular: is Lebesgue integrable over if and only if is absolutely Gauge integrable over , i.e. H. both the function and its amount are integrable across the gauge. ${\displaystyle E}$ ${\displaystyle f\colon E\rightarrow \mathbb {R} }$ ${\displaystyle E}$ ${\displaystyle f}$ ${\displaystyle E}$ ${\displaystyle f}$ ${\displaystyle E}$ ${\displaystyle f}$ ${\displaystyle E}$ ${\displaystyle f}$ ${\displaystyle |f|}$ ${\displaystyle E}$

This means that the Lebesgue integral is also included as a special case in the gauge integral.

The multi-dimensional gauge integral

The gauge integral is similarly continued to any dimensions. As in a dimension, the integral is first defined using intervals. The extension to infinitely large intervals should already be included.

• Definition (n-dimensional interval): A set is called (n-dimensional) interval if there are intervals with . ${\displaystyle I\subset {\overline {\mathbb {R} }}^{n}}$ ${\displaystyle J_{1},\dots ,J_{n}\subset {\overline {\mathbb {R} }}}$ ${\displaystyle I=J_{1}\times \dots \times J_{n}}$

An interval in n dimensions is thus defined as the Cartesian product of n one-dimensional intervals and consequently has the shape of an n-dimensional cuboid . The following applies:

• Definition (open, closed): An interval is open [closed] in , if all open [closed] in are. ${\displaystyle I=J_{1}\times \dots \times J_{n}}$ ${\displaystyle {\overline {\mathbb {R} }}^{n}}$ ${\displaystyle J_{i}}$ ${\displaystyle {\overline {\mathbb {R} }}}$

Note that an interval of the form with or is also referred to as closed in . ${\displaystyle [a,b]}$ ${\displaystyle a=-\infty }$ ${\displaystyle b=\infty }$ ${\displaystyle {\overline {\mathbb {R} }}}$

Figure 8 : A marked decomposition of a closed 2-dimensional interval. Such a decomposition is called -fine, if . ${\displaystyle D=\{(t_{1},I_{1}),\dots ,(t_{15},I_{15})\}}$ ${\displaystyle \gamma }$ ${\displaystyle [x_{i-1},x_{i}]\subset \gamma (t_{i})}$

The terms of the highlighted decomposition and the calibration function are expanded accordingly to include dimensions: ${\displaystyle n}$

• Definition (highlighted decomposition): Let be a closed interval. A lot is marked decomposition of , if all intervals with and . ${\displaystyle I\subset {\overline {\mathbb {R} }}^{n}}$ ${\displaystyle D=\{(t_{i},I_{i}),i=1,\dots ,n\}}$ ${\displaystyle I}$ ${\displaystyle I_{i}}$ ${\displaystyle t_{i}\in I_{i}}$ ${\displaystyle \cup _{i=1}^{n}I_{i}=I}$

A marked decomposition of a closed interval is therefore a set of ordered pairs , whose first entry is a point and whose second entry, on the other hand, is an interval. The point belonging to the interval must be in , and the union of all results in the interval to be broken down (see Fig. 8). ${\displaystyle (t_{i},I_{i})}$ ${\displaystyle I\subset {\overline {\mathbb {R} }}^{n}}$ ${\displaystyle I_{i}}$ ${\displaystyle t_{i}}$ ${\displaystyle I_{i}}$ ${\displaystyle I_{i}}$ ${\displaystyle I}$

• Definition (calibration function): Let be an interval. A intervallwertige function is called calibration function on , if an open interval and for all . ${\displaystyle I\subset {\overline {\mathbb {R} }}^{n}}$ ${\displaystyle \gamma }$ ${\displaystyle I}$ ${\displaystyle \gamma (t)}$ ${\displaystyle t\in \gamma (t)}$ ${\displaystyle t\in I}$

As in the one-dimensional, an interval should also be considered open if it has the form or with any real number . Just as in a dimension, these terms are used to define the fineness of a marked decomposition: ${\displaystyle I=J_{1}\times \dots \times J_{n}}$ ${\displaystyle J_{i}}$ ${\displaystyle J_{i}=[-\infty ,a)}$ ${\displaystyle J_{i}=(a,\infty ]}$ ${\displaystyle a}$

• Definition: Let be a calibration function on the closed interval . A marked decomposition is called -fine, if for . ${\displaystyle \gamma }$ ${\displaystyle I}$ ${\displaystyle D=\{(t_{i},I_{i}):i=1,\dots ,n\}}$ ${\displaystyle \gamma }$ ${\displaystyle I_{i}\subset \gamma (t_{i})}$ ${\displaystyle i=1,\dots ,n}$

The volume of an interval is given by ${\displaystyle I}$

${\displaystyle \operatorname {vol} (I):=v(J_{1}\times \dots \times J_{n})=l(J_{1})\cdot l(J_{2})\cdot \dots \cdot l(J_{n}),}$

where represents the length of the (one-dimensional) interval . The convention should also apply here, i. h, has. one of the length , it is , even if one or more infinitely long intervals among the are. ${\displaystyle l(J_{i})=l([b_{i},a_{i}])=b_{i}-a_{i}}$ ${\displaystyle J_{i}}$ ${\displaystyle 0\cdot \infty =0}$ ${\displaystyle J_{i}}$ ${\displaystyle 0}$ ${\displaystyle v(I)=0}$ ${\displaystyle J_{i}}$

Each function is continued on: ${\displaystyle f\colon I\subset \mathbb {R} ^{n}\rightarrow \mathbb {R} }$ ${\displaystyle {\overline {\mathbb {R} }}^{n}}$

${\displaystyle {\bar {f}}(x)={\begin{cases}f(x)&{\text{ falls }}x\in I\\0&{\text{ sonst }}\end{cases}}}$

In particular, it vanishes in every point that has at least one infinite component. So is about . Riemann subtotals for a function and a highlighted decomposition are defined by: ${\displaystyle {\bar {f}}}$ ${\displaystyle x=(x_{1},\dots ,x_{n})\in {\overline {\mathbb {R} }}^{n}}$ ${\displaystyle {\bar {f}}(1,\infty ,0,-\infty ,\dots )=0}$ ${\displaystyle S({\bar {f}},D)}$ ${\displaystyle f\colon I\rightarrow \mathbb {R} }$ ${\displaystyle D=\{(t_{i},I_{i}):i=1,\dots ,n\}}$

${\displaystyle S({\bar {f}},D)=\sum _{i=1}^{n}{\bar {f}}(t_{i})\operatorname {vol} (I_{i})}$

The convention is also valid here. The gauge integral in dimensions can then be set as follows: ${\displaystyle 0\cdot \infty =0}$ ${\displaystyle n}$

• Definition (n-dimensional gauge integral): Whether an interval of , its degree in . 's gauge integrable (Henstock- (Kurzweil-) -intergrabel, eichintegrabel) above , if there is a fixed number and each a calibration function on are such that for each -fine marked decomposition applies: . One writes: . ${\displaystyle I}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle {\overline {I}}}$ ${\displaystyle {\overline {\mathbb {R} }}^{n}}$ ${\displaystyle f}$ ${\displaystyle I}$ ${\displaystyle A}$ ${\displaystyle \epsilon >0}$ ${\displaystyle \gamma }$ ${\displaystyle {\bar {I}}}$ ${\displaystyle \gamma }$ ${\displaystyle D}$ ${\displaystyle |S({\bar {f}},D)-A|<\epsilon }$ ${\displaystyle A=\int _{I}^{\,}f}$

All expansions to any measurable subsets of the happen exactly as with the one-dimensional gauge integral. The above Properties of the one-dimensional gauge integral are transferred analogously to the multi-dimensional gauge integral. Furthermore, versions of the theorems of Fubini and Tonelli can be set up for the n-dimensional gauge integral. ${\displaystyle \mathbb {R} ^{n}}$

characterization

The gauge integral is descriptive in nature, i. that is, it is based on the observation that differentiation and integration are usually interchangeable. With this observation in the foreground, the calibration integral guarantees interchangeability in general. There are therefore immediately (without having to use pathological examples) functions that are not Riemann integrable but Gauge integrable, such as B. the reciprocal of the root function or the leading example above.

Literature and web links

• Ralph Henstock: Theories of Integration. London 1963.
• Douglas S. Kurtz, Charles W. Swartz: Theories of Integration. 2004.
• Website about the gauge integral