One-sample t test

The sample t-test (engl. One sample t-test ) is a test of significance from the mathematical statistics . Using the mean value of a random sample , it checks whether the mean value of a population is equal to a specified value (or smaller or larger).

A corresponding extension of a comparison of means for two (dependent or independent) samples is the two-sample t-test .

Test idea

The one-sample t-test uses the mean of a sample to check (in the simplest case) whether the mean of the population differs from a given value . ${\displaystyle {\bar {x}}}$ ${\displaystyle \mu }$ ${\displaystyle \mu _{0}}$

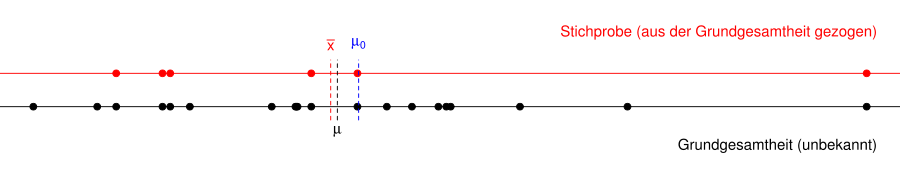
The graphic below shows a population (black dots) and a sample (red dots) that were randomly drawn from the population. The sample mean can be calculated from the sample, but the population mean is unknown. One suspects z. B. because of historical results or theoretical considerations that the mean of the population is different from a given value . ${\displaystyle {\bar {x}}}$ ${\displaystyle \mu }$ ${\displaystyle \mu }$ ${\displaystyle \mu _{0}}$

In the simplest case, the test checks

• the null hypothesis that the population mean equals the given value ( ) ${\displaystyle H_{0}:\,\mu =\mu _{0}}$
• against the alternative hypothesis that the mean of the population is not equal to the given value ( ). ${\displaystyle H_{1}:\,\mu \neq \mu _{0}}$

If the sample is appropriately drawn, e.g. For example, as a simple random sample , there is a high probability that the mean of the sample will be close to the mean of the population . I.e. the distance between the dashed red and black lines will most likely be small. ${\displaystyle {\bar {x}}}$ ${\displaystyle \mu }$

• If the specified value is now close to the mean value of the sample , i.e. H. the dashed blue and dashed red lines have a small distance, then the specified value is also close to the mean value of the population . We cannot then reject the null hypothesis. ${\displaystyle \mu _{0}}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle \mu _{0}}$ ${\displaystyle \mu }$
• However, if the specified value is far from the mean value of the sample , i.e. H. the dashed blue and dashed red lines have a large distance, then the specified value is also far away from the mean value of the population . Then we can reject the null hypothesis. ${\displaystyle \mu _{0}}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle \mu _{0}}$ ${\displaystyle \mu }$

The exact mathematical calculations can be found in the following sections.

Hypotheses

For the one-sample t-test, three different hypothesis pairs (null hypothesis vs. alternative hypothesis ) can be formulated: ${\displaystyle H_{0}}$ ${\displaystyle H_{1}}$

1. ${\displaystyle H_{0}:\,\mu =\mu _{0}}$vs. (two-sided test), ${\displaystyle H_{1}:\,\mu \neq \mu _{0}}$
2. ${\displaystyle H_{0}:\,\mu \leq \mu _{0}}$vs. (right-sided test) and ${\displaystyle H_{1}:\,\mu >\mu _{0}}$
3. ${\displaystyle H_{0}:\,\mu \geq \mu _{0}}$vs. (left side test), ${\displaystyle H_{1}:\,\mu <\mu _{0}}$

The same test statistic is used for all three hypothesis pairs , only the areas for the rejection or acceptance of the null hypothesis differ.

Mathematical derivation of the test statistic

For a normally distributed population

If there are independent, normally distributed random variables with expected value and standard deviation , and if you want to test the null hypothesis , then it makes sense to use their arithmetic mean ${\displaystyle X_{1},X_{2},\dots ,X_{n}}$ ${\displaystyle \mu \in \mathbb {R} }$ ${\displaystyle \sigma >0}$ ${\displaystyle \mu =\mu _{0}}$

${\displaystyle {\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}}$

to use as test statistic . Namely, it is also normally distributed with an expected value , but has the standard deviation . If it is known , the hypothesis could be tested with a Gaussian test . For this one calculates ${\displaystyle \mu }$ ${\displaystyle {\tfrac {\sigma }{\sqrt {n}}}}$ ${\displaystyle \sigma }$

${\displaystyle Z={\sqrt {n}}{\frac {{\bar {X}}-\mu _{0}}{\sigma }}}$,

which is standard normally distributed under the null hypothesis.

Normally, however, the standard deviation is unknown and appears here as a so-called interference parameter (since there is no inference here) . In this case it stands to reason to use the empirical standard deviation ${\displaystyle \sigma }$

${\displaystyle S={\sqrt {\frac {\sum _{i=1}^{n}(X_{i}-{\bar {X}})^{2}}{n-1}}}}$

to estimate and as test statistic

${\displaystyle T={\sqrt {n}}{\frac {{\bar {X}}-\mu _{0}}{S}}}$

to use. Under the null hypothesis, however, this statistic is no longer normally distributed, but t-distributed with degrees of freedom . If the value of the test statistic for a specific sample is so large (or so small) that this or an even more significant value is sufficiently improbable under the null hypothesis , the null hypothesis is rejected. ${\displaystyle n-1}$

For an arbitrarily distributed population

If ( ) are independently and identically distributed random variables with expected value and standard deviation , then, as in the above case, it is obvious to use their arithmetic mean ${\displaystyle X_{1},X_{2},\dots ,X_{n}}$ ${\displaystyle n>30}$ ${\displaystyle \mu \in \mathbb {R} }$ ${\displaystyle \sigma >0}$

${\displaystyle {\bar {X}}={\frac {1}{n}}\sum _{i=1}^{n}X_{i}}$

to use as test statistic . Although the distribution of is unknown, the central limit theorem means that it is approximately normally distributed with expected value and standard deviation . ${\displaystyle {\bar {X}}}$ ${\displaystyle \mu }$ ${\displaystyle {\tfrac {\sigma }{\sqrt {n}}}}$

Because the standard deviation is normally unknown, it is obvious in this case to use the empirical standard deviation as well

${\displaystyle S={\sqrt {\frac {\sum _{i=1}^{n}(X_{i}-{\bar {X}})^{2}}{n-1}}}}$

to estimate and again as test statistic

${\displaystyle T={\sqrt {n}}{\frac {{\bar {X}}-\mu _{0}}{S}}}$

to use. Under the null hypothesis, however, this statistic is only approximately t-distributed with degrees of freedom. If the value of the test statistic for a specific sample is so large (or so small) that this or an even more extreme value is sufficiently improbable under the null hypothesis , the null hypothesis is rejected. ${\displaystyle n-1}$

example

Two-sided test

The aim is to test whether the average runtime of notebook batteries deviates from the 3.5 hours specified by the manufacturer. For this purpose, the running times of 10 batteries of this brand are measured under controlled identical conditions. Since we have few observations, the central limit theorem cannot be applied; see section Mathematical Derivation of Test Statistics for an Arbitrarily Distributed Population . We must therefore assume that the runtime of the notebook batteries is normally distributed in the population. ${\displaystyle \mu }$

The following hypotheses should be tested:

General	example
${\displaystyle H_{0}:\,\mu =\mu _{0}}$ vs. ${\displaystyle H_{1}:\,\mu \neq \mu _{0}}$	${\displaystyle H_{0}:\,\mu =3{,}5}$Hours vs. Hours ${\displaystyle H_{1}:\,\mu \neq 3{,}5}$

For example, performing the test would give the sample mean hours and sample standard deviation hours. The test value can now be calculated from this as follows: ${\displaystyle {\bar {x}}=3{,}25}$ ${\displaystyle s=0{,}31}$ ${\displaystyle t}$

General	example
${\displaystyle t={\sqrt {n}}{\frac {{\bar {x}}-\mu _{0}}{s}}}$	${\displaystyle t={\sqrt {10}}{\frac {3{,}25-3{,}5}{0{,}31}}\approx -2{,}55}$
With ${\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$	${\displaystyle {\bar {x}}=3{,}25}$ Hours
and ${\displaystyle s={\sqrt {\frac {\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}{n-1}}}}$	${\displaystyle s=0{,}31}$ Hours

The null hypothesis is rejected at the significance level , if . Therein corresponds to the - quantile of the t-distribution with degrees of freedom. ${\displaystyle \alpha }$ ${\displaystyle |t|>t(1-{\tfrac {\alpha }{2}},n-1)}$ ${\displaystyle t(1-{\tfrac {\alpha }{2}},n-1)}$ ${\displaystyle (1-{\tfrac {\alpha }{2}})}$ ${\displaystyle n-1}$

For the example, this means that the null hypothesis is rejected at a significance level if t is less than the 2.5% quantile or greater than the 97.5% quantile of the t-distribution with degrees of freedom. The value can be found with the help of a t-table or a computer program . Because of the symmetry of the t-distribution is . Because of the null hypothesis that the expected value of the running time is equal to 3.5 hours, it can be rejected at the level of significance . The batteries do not run for an average of 3.5 hours, i.e. more or less. ${\displaystyle \alpha =5\,\%}$ ${\displaystyle 10-1=9}$ ${\displaystyle t(0{,}975;9)=2{,}262}$ ${\displaystyle t(0{,}025;9)=-2{,}262}$ ${\displaystyle t=-2{,}55<-2{,}262}$ ${\displaystyle \alpha =5\,\%}$

One-sided test

In practice, a one-sided test would have been carried out, because the customer is only satisfied if the batteries run for more than 3.5 hours. The hypotheses for checking whether the batteries can hold out for at least 3.5 hours are then

General	example
${\displaystyle H_{0}:\,\mu \geq \mu _{0}}$ vs. ${\displaystyle H_{1}:\,\mu <\mu _{0}}$	${\displaystyle H_{0}:\,\mu \geq 3{,}5}$Hours vs. Hours ${\displaystyle H_{1}:\,\mu <3{,}5}$

The test value is given again and can also be used to test the one-sided hypothesis on the level of significance . The null hypothesis is now rejected if is. ${\displaystyle t\approx -2{,}55}$ ${\displaystyle \alpha }$ ${\displaystyle \mu \geq \mu _{0}}$ ${\displaystyle t<-t(1-\alpha ,\ n-1)}$

For results . And then we can reject this null hypothesis as well, i.e. In other words, we were able to show that the average battery life is less than 3.5 hours. ${\displaystyle \alpha =0{,}05}$ ${\displaystyle t(1-\alpha ,\ n-1)=1{,}833}$ ${\displaystyle -2{,}55<-1{,}833}$

Alternative tests

• In the case,

• if the central limit theorem for the sample variables is not met, or ${\displaystyle X_{i}}$
• if the central limit theorem for the sample variables is met and the sample size is less than or equal to 30 ${\displaystyle X_{i}}$

As an alternative, the nonparametric single sample median test can be used. However, this tests whether the median of the population corresponds to a specified value.

• If the standard deviation is known, the one- sample Gaussian test should be used. ${\displaystyle \sigma }$

Compact display

One-sample t-test
requirements	${\displaystyle X_{i}\,}$ independent of each other ${\displaystyle X_{i}\sim {\mathcal {N}}(\mu ;\sigma )\,}$or and sufficiently large (see ZGS ) ${\displaystyle X_{i}\sim (\mu ;\sigma )\,}$ ${\displaystyle n}$
Hypotheses	${\displaystyle H_{0}:\mu \leq \mu _{0}}$ ${\displaystyle H_{1}:\mu >\mu _{0}\,}$ (right side)	${\displaystyle H_{0}:\mu =\mu _{0}\,}$ ${\displaystyle H_{1}:\mu \neq \mu _{0}}$ (two-sided)	${\displaystyle H_{0}:\mu \geq \mu _{0}}$ ${\displaystyle H_{1}:\mu <\mu _{0}\,}$ (left side)
Test statistics	${\displaystyle T={\sqrt {n}}{\frac {{\bar {X}}-\mu _{0}}{S}}\sim t_{n-1}}$
Test value	${\displaystyle t={\sqrt {n}}{\frac {{\bar {x}}-\mu _{0}}{s}}}$with and ${\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$ ${\displaystyle s={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\bar {x}})^{2}}}}$
Rejection area ${\displaystyle H_{0}}$	${\displaystyle (t_{1-\alpha ;n-1},\infty )\,}$	${\displaystyle (-\infty ,-t_{1-{\frac {\alpha }{2}};n-1})\cup (t_{1-{\frac {\alpha }{2}};n-1},\infty )\,}$	${\displaystyle (-\infty ,-t_{1-\alpha ;n-1})\,}$

literature

• Jürgen Bortz , Christof Schuster: Statistics for human and social scientists . 7th edition. Springer, Berlin 2010, ISBN 978-3-642-12769-4 .
• Jürgen Bortz , Gustav A. Lienert, Klaus Boehnke: Distribution-free methods in biostatistics . 3. Edition. Springer Berlin Heidelberg, 2008, ISBN 978-3-540-74706-2 .
• Christel Weiß: Basic knowledge of medical statistics . 5th edition. Springer, Berlin 2010, ISBN 978-3-642-11336-9 .

Web links

• Calculator for all variants of the t-test. Calculates t-value, p-value and critical values.
• Internet calculator - T distribution