Two sample t test

The two-sample t-test is a significance test from mathematical statistics . In the usual form, it uses the mean values ​​of two samples to check whether the mean values ​​of two populations are the same or different from one another.

There are two flavors of the two-sample t-test:

• those for two independent samples with equal standard deviations in both populations and ${\displaystyle \sigma }$
• those for two dependent samples.

If there are two independent samples with unequal standard deviations in both populations, the Welch test must be used.

Basic idea

The two-sample t-test uses the mean values and two samples to check (in the simplest case) whether the mean values and the associated populations are different. ${\displaystyle {\overline {x}}_{1}}$ ${\displaystyle {\overline {x}}_{2}}$ ${\displaystyle \mu _{1}}$ ${\displaystyle \mu _{2}}$

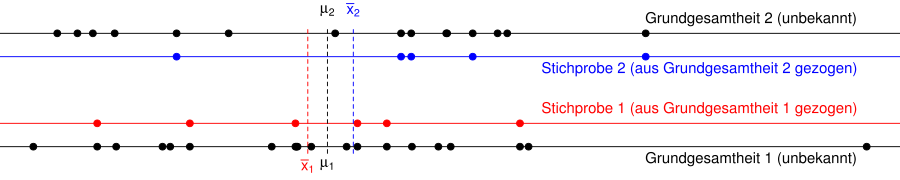
The graph below shows two populations (black dots) and two samples (blue and red dots) that were randomly drawn from the populations. The mean values ​​of the samples and can be calculated from the samples, but the mean values ​​of the populations and are unknown. The graph shows the populations are so constructed that the two means are equal, so . ${\displaystyle {\overline {x}}_{1}}$ ${\displaystyle {\overline {x}}_{2}}$ ${\displaystyle \mu _{1}}$ ${\displaystyle \mu _{2}}$ ${\displaystyle \mu _{1}=\mu _{2}}$

We now suspect z. B. on the basis of historical results or theoretical considerations that the mean values and the population are different, and would like to check this. ${\displaystyle \mu _{1}}$ ${\displaystyle \mu _{2}}$

In the simplest case, the two-sample t-test checks

• the null hypothesis that population means are equal ( ) ${\displaystyle H_{0}:\,\mu _{1}=\mu _{2}}$
• against the alternative hypothesis that the population means are unequal ( ). ${\displaystyle H_{1}:\,\mu _{1}\neq \mu _{2}}$

If the samples are appropriately drawn, for example as simple random samples , the mean of sample 1 will be very likely to be close to the mean of population 1 and the mean of sample 2 will be very likely to be close to the mean of population 2. That is, the distance between the dashed red and black lines or the dashed blue and black lines will most likely be small. ${\displaystyle {\overline {x}}_{1}}$ ${\displaystyle \mu _{1}}$ ${\displaystyle {\overline {x}}_{2}}$ ${\displaystyle \mu _{2}}$

• If the distance between and (dashed blue and red line) is small, then are the mean values of the populations and close together. We cannot reject the null hypothesis. ${\displaystyle {\overline {x}}_{1}}$ ${\displaystyle {\overline {x}}_{2}}$ ${\displaystyle \mu _{1}}$ ${\displaystyle \mu _{2}}$
• If the distance between and (dashed blue or red line) is large, then the mean values ​​of the populations and are also far apart. We can reject the null hypothesis. ${\displaystyle {\overline {x}}_{1}}$ ${\displaystyle {\overline {x}}_{2}}$ ${\displaystyle \mu _{1}}$ ${\displaystyle \mu _{2}}$

The exact mathematical calculations can be found in the following sections.

Two-sample t-test for independent samples

The two-sample t-test is used to examine differences in mean values ​​between two populations with the same unknown standard deviation . For this, each of the populations must be normally distributed or the sample sizes must be large enough for the central limit theorem to be applicable. For the test, a sample of the size is drawn from the 1st population and, independently of this, a sample of the size from the 2nd population. For the associated independent sample variables and then applies and with the means and the two populations. If a number is given for the difference between the mean values, then the null hypothesis is ${\displaystyle \sigma }$ ${\displaystyle x_{1},\ldots ,x_{n}}$ ${\displaystyle n}$ ${\displaystyle y_{1},\ldots ,y_{m}}$ ${\displaystyle m}$ ${\displaystyle X_{1},\ldots ,X_{n}}$ ${\displaystyle Y_{1},\ldots ,Y_{m}}$ ${\displaystyle \operatorname {E} (X)(X_{i})=\mu _{X}}$ ${\displaystyle \operatorname {E} (X)(Y_{j})=\mu _{Y}}$ ${\displaystyle \mu _{X}}$ ${\displaystyle \mu _{Y}}$ ${\displaystyle \omega _{0}}$

${\displaystyle H_{0}:\,\mu _{X}-\mu _{Y}=\omega _{0}}$

and the alternative hypothesis

${\displaystyle H_{1}:\,\mu _{X}-\mu _{Y}\neq \omega _{0}}$.

The test statistic results in

${\displaystyle T={\frac {{\overline {X}}-{\overline {Y}}-\omega _{0}}{S{\sqrt {{\frac {1}{n}}+{\frac {1}{m}}}}}}={\sqrt {\frac {nm}{n+m}}}{\frac {{\overline {X}}-{\overline {Y}}-\omega _{0}}{S}}.}$

There are and the respective sample mean values ​​and ${\displaystyle {\overline {X}}}$ ${\displaystyle {\overline {Y}}}$

${\displaystyle S^{2}={\frac {(n-1)S_{X}^{2}+(m-1)S_{Y}^{2}}{n+m-2}}}$

the weighted variance, calculated as the weighted mean of the respective sample variances and . ${\displaystyle S_{X}^{2}}$ ${\displaystyle S_{Y}^{2}}$

The test statistic is t-distributed with degrees of freedom under the null hypothesis . The test value, i.e. the realization of the test statistics based on the sample, is then calculated as ${\displaystyle T}$ ${\displaystyle m+n-2}$

${\displaystyle t={\sqrt {\frac {nm}{n+m}}}{\frac {{\overline {x}}-{\overline {y}}-\omega _{0}}{s}}.}$

Where and are the mean values ​​and calculated from the sample ${\displaystyle {\overline {x}}}$ ${\displaystyle {\overline {y}}}$

${\displaystyle s^{2}={\frac {(n-1)s_{x}^{2}+(m-1)s_{y}^{2}}{n+m-2}}}$

the realization of the weighted variance, calculated from the sample variances and . It is also known as pooled sample variance . ${\displaystyle s_{x}^{2}}$ ${\displaystyle s_{y}^{2}}$

At the level of significance , the null hypothesis is rejected in favor of the alternative, if ${\displaystyle \alpha }$

${\displaystyle |t|>t(1-{\tfrac {1}{2}}\alpha ,\ n+m-2).}$

Alternatively, the following hypotheses can be tested with the same test statistic : ${\displaystyle T}$

• ${\displaystyle \!H_{0}:\mu _{X}-\mu _{Y}\leq \omega _{0}}$vs. and the null hypothesis is rejected if resp. ${\displaystyle \!H_{1}:\mu _{X}-\mu _{Y}>\omega _{0}}$ ${\displaystyle t>t(1-\alpha ,\ m+n-2)}$
• ${\displaystyle \!H_{0}:\mu _{X}-\mu _{Y}\geq \omega _{0}}$vs. and the null hypothesis is rejected if . ${\displaystyle \!H_{1}:\mu _{X}-\mu _{Y}<\omega _{0}}$ ${\displaystyle t<-t(1-\alpha ,\ m+n-2)}$

comment

If the variances in the populations are not equal, then the Welch test must be carried out.

example 1

Two types of fertilizer are to be compared. For this purpose, 25 plots of the same size are fertilized, namely  plots with variety A and  plots with variety B. It is assumed that the harvest yields are normally distributed with the same variances. The former results in a mean crop yield with sample variance and the other plots the mean with variance . This is used to calculate the weighted variance ${\displaystyle n=10}$ ${\displaystyle m=15}$ ${\displaystyle {\overline {x}}=23{,}6}$ ${\displaystyle s_{x}^{2}=9{,}5}$ ${\displaystyle {\overline {y}}=20{,}1}$ ${\displaystyle s_{y}^{2}=8{,}9}$

${\displaystyle s^{2}={\frac {9\cdot 9{,}5+14\cdot 8{,}9}{10+15-2}}=9{,}135}$.

The test variable is obtained from this

${\displaystyle t={\sqrt {\frac {10\cdot 15}{10+15}}}\cdot {\frac {23{,}6-20{,}1}{\sqrt {9{,}135}}}=2{,}837}$.

This value is greater than the 0.975 quantile of the t-distribution with degrees of freedom . So it can be said with a confidence of that there is a difference in the effect of the two fertilizers. ${\displaystyle 10+15-2=23}$ ${\displaystyle t(0{,}975;\ 23)=2{,}069}$ ${\displaystyle 95\,\%}$

Compact display

Two-sample t-test for two independent samples
requirements	${\displaystyle X_{1},\ldots ,X_{n}}$and independent of each other ${\displaystyle Y_{1}\ldots ,Y_{m}}$ ${\displaystyle X_{i}\sim {\mathcal {N}}(\mu _{X};\sigma )\,}$or with ${\displaystyle X_{i}\sim (\mu _{X};\sigma )\,}$ ${\displaystyle n>30}$ ${\displaystyle Y_{j}\sim {\mathcal {N}}(\mu _{Y};\sigma )\,}$or with ${\displaystyle Y_{j}\sim (\mu _{Y};\sigma )\,}$ ${\displaystyle m>30}$ ${\displaystyle \sigma }$ unknown
Hypotheses	${\displaystyle H_{0}:\mu _{X}-\mu _{Y}\leq \omega _{0}\,}$ ${\displaystyle H_{1}:\mu _{X}-\mu _{Y}>\omega _{0}\,}$ (right side)	${\displaystyle H_{0}:\mu _{X}-\mu _{Y}=\omega _{0}\,}$ ${\displaystyle H_{1}:\mu _{X}-\mu _{Y}\neq \omega _{0}\,}$ (two-sided)	${\displaystyle H_{0}:\mu _{X}-\mu _{Y}\geq \omega _{0}\,}$ ${\displaystyle H_{1}:\mu _{X}-\mu _{Y}<\omega _{0}\,}$ (left side)
Test statistics	${\displaystyle T={\sqrt {\frac {nm}{n+m}}}{\frac {{\overline {X}}-{\overline {Y}}-\omega _{0}}{S}}\sim t_{n+m-2}}$
Test value	${\displaystyle t={\sqrt {\frac {nm}{n+m}}}{\frac {{\overline {x}}-{\overline {y}}-\omega _{0}}{s}}}$ with , , , ${\displaystyle {\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$ ${\displaystyle {\overline {y}}={\frac {1}{m}}\sum _{i=1}^{m}y_{i}}$ ${\displaystyle s_{x}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}}}$ ${\displaystyle s_{y}={\sqrt {{\frac {1}{m-1}}\sum _{j=1}^{m}(y_{j}-{\overline {y}})^{2}}}}$ and ${\displaystyle s={\sqrt {\frac {(n-1)s_{x}^{2}+(m-1)s_{y}^{2}}{n+m-2}}}}$
Rejection area ${\displaystyle H_{0}}$	${\displaystyle \{t|t>t_{1-\alpha ;n+m-2}\}\,}$	${\displaystyle \{t|t<-t_{1-\alpha /2;n+m-2}\}\,}$ or ${\displaystyle \{t|t>t_{1-\alpha /2;n+m-2}\}\,}$	${\displaystyle \{t|t<-t_{1-\alpha ;n+m-2}\}\,}$

Two-sample t-test for dependent samples

Error 1. Type of connected and disconnected t-test depending on the correlation . The simulated random numbers come from a bivariate normal distribution with a variance of 1. The significance level is 5% and the sample size is 60.

Goodness of connected and unconnected t-test as a function of the correlation. The simulated random numbers come from a bivariate normal distribution with a variance of 1 and a difference between the expected values of 0.4. The level of significance is 5% and the sample size is 60.

Here and are two random samples, connected in pairs, which were obtained, for example, from two measurements on the same examination units (repeated measurements). The samples can also be paired for other reasons, for example if the and values ​​are measured by women or men in a partnership and differences between the sexes are of interest. ${\displaystyle x_{1},x_{2},\dots ,x_{n}}$ ${\displaystyle y_{1},y_{2},\dots ,y_{n}}$ ${\displaystyle x}$ ${\displaystyle y}$

If the null hypothesis is to be tested that the two expected values ​​of the underlying normally distributed populations are the same, the differences can be tested for zero with the one- sample t-test . In practice, with smaller sample sizes ( ), the prerequisite must be met that the differences in the population are normally distributed. With sufficiently large samples, the differences between the pairs are distributed approximately normally around the arithmetic mean of the difference in the population. Overall, the t-test reacts rather robustly to an assumption violation. ${\displaystyle d_{i}=x_{i}-y_{i}}$ ${\displaystyle n\leq 30}$

Example 2

In order to test a new therapy for lowering the cholesterol level, the cholesterol levels are determined in ten test subjects before and after the treatment. The following measurement results are obtained:

Before treatment:	223	259	248	220	287	191	229	270	245	201
After treatment:	220	244	243	211	299	170	210	276	252	189
Difference:	3	15th	5	9	−12	21st	19th	−6	−7	12

The differences in the measured values ​​have the arithmetic mean and the sample standard deviation . This results as a test variable value ${\displaystyle {\overline {d}}=5{,}9}$ ${\displaystyle s_{d}=11{,}3866}$

${\displaystyle t={\sqrt {10}}{\frac {5{,}9}{11{,}3866}}=1{,}6385}$.

It is , therefore, applies . Thus, the null hypothesis that the expected values ​​of the cholesterol values ​​before and after the treatment are the same, i.e. that the therapy has no effect , cannot be rejected at the level of significance . Because of this , the one-sided alternative that the therapy lowers the cholesterol level is not significant either. If the treatment has any effect at all, it is not big enough to detect with such a small sample size. ${\displaystyle t(0{,}975;\ 9)=2{,}2622}$ ${\displaystyle |t|\leq t(0{,}975;\ 9)}$ ${\displaystyle \alpha =5\,\%}$ ${\displaystyle t<t(0{,}95;\ 9)=1{,}8331}$

Compact display

Two-sample t-test for two paired samples
requirements	${\displaystyle D_{i}=X_{i}-Y_{i}\,}$ independent of each other ${\displaystyle {\overline {D}}={\frac {1}{n}}\sum _{i=1}^{n}D_{i}\sim {\mathcal {N}}(\mu _{D};\sigma _{D}/{\sqrt {n}})}$ (at least approximately)
Hypotheses	${\displaystyle H_{0}:\mu _{X}-\mu _{Y}\leq \omega _{0}}$ ${\displaystyle H_{1}:\mu _{X}-\mu _{Y}>\omega _{0}\,}$ (right side)	${\displaystyle H_{0}:\mu _{X}-\mu _{Y}=\omega _{0}\,}$ ${\displaystyle H_{1}:\mu _{X}-\mu _{Y}\neq \omega _{0}}$ (two-sided)	${\displaystyle H_{0}:\mu _{X}-\mu _{Y}\geq \omega _{0}}$ ${\displaystyle H_{1}:\mu _{X}-\mu _{Y}<\omega _{0}\,}$ (left side)
Test statistics	${\displaystyle T={\sqrt {n}}{\frac {{\overline {D}}-\omega _{0}}{S_{D}}}\sim t_{n-1}}$
Test value	${\displaystyle t={\sqrt {n}}{\frac {{\overline {d}}-\omega _{0}}{s_{d}}}}$ with , , and ${\displaystyle d_{i}=x_{i}-y_{i}\,}$ ${\displaystyle {\overline {d}}={\frac {1}{n}}\sum _{i=1}^{n}d_{i}}$ ${\displaystyle s_{d}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}(d_{i}-{\overline {d}})^{2}}}}$
Rejection area ${\displaystyle H_{0}}$	${\displaystyle [t_{1-\alpha ;n-1},\infty )\,}$	${\displaystyle (-\infty ,-t_{1-{\frac {\alpha }{2}};n-1}]\cup [t_{1-{\frac {\alpha }{2}};n-1},\infty )\,}$	${\displaystyle (-\infty ,-t_{1-\alpha ;n-1}]\,}$

Welch test

The Welch test calculates the test statistic similar to the two-sample t-test:

${\displaystyle T={\frac {{\overline {X}}-{\overline {Y}}-\omega _{0}}{\sqrt {{\frac {S_{X}^{2}}{n}}+{\frac {S_{Y}^{2}}{m}}}}}\approx t_{\nu }.}$

However, this test statistic is not distributed under the null hypothesis , but is approximated by means of a t-distribution with a modified number of degrees of freedom (see also Behrens-Fisher problem ): ${\displaystyle t}$

${\displaystyle \nu ={\left({\frac {s_{x}^{2}}{n}}+{\frac {s_{y}^{2}}{m}}\right)^{2} \over {\frac {1}{n-1}}\left({\frac {s_{x}^{2}}{n}}\right)^{2}+{\frac {1}{m-1}}\left({\frac {s_{y}^{2}}{m}}\right)^{2}}.}$

Where and are the standard deviations of the populations estimated from the sample as well as and the sample sizes. ${\displaystyle s_{x}}$ ${\displaystyle s_{y}}$ ${\displaystyle n}$ ${\displaystyle m}$

Although the Welch test was developed specifically for the case , the test does not work well if at least one of the distributions is abnormal, the case numbers are small and very different ( ). ${\displaystyle \sigma _{X}\neq \sigma _{Y}}$ ${\displaystyle n\neq m}$

Compact display

Welch test
requirements	${\displaystyle X_{1},\ldots ,X_{n}}$and independent of each other ${\displaystyle Y_{1}\ldots ,Y_{m}}$ ${\displaystyle X_{i}\sim {\mathcal {N}}(\mu _{X};\sigma _{X})\,}$or with ${\displaystyle X_{i}\sim (\mu _{X};\sigma _{X})\,}$ ${\displaystyle n>30}$ ${\displaystyle Y_{j}\sim {\mathcal {N}}(\mu _{Y};\sigma _{Y})\,}$or with ${\displaystyle Y_{j}\sim (\mu _{Y};\sigma _{Y})\,}$ ${\displaystyle m>30}$ ${\displaystyle \sigma _{X}\neq \sigma _{Y}}$ unknown
Hypotheses	${\displaystyle H_{0}:\mu _{X}-\mu _{Y}\leq \omega _{0}\,}$ ${\displaystyle H_{1}:\mu _{X}-\mu _{Y}>\omega _{0}\,}$ (right side)	${\displaystyle H_{0}:\mu _{X}-\mu _{Y}=\omega _{0}\,}$ ${\displaystyle H_{1}:\mu _{X}-\mu _{Y}\neq \omega _{0}\,}$ (two-sided)	${\displaystyle H_{0}:\mu _{X}-\mu _{Y}\geq \omega _{0}\,}$ ${\displaystyle H_{1}:\mu _{X}-\mu _{Y}<\omega _{0}\,}$ (left side)
Test statistics	${\displaystyle T={\frac {{\overline {X}}-{\overline {Y}}-\omega _{0}}{S}}\approx t_{\nu }}$
Test value	${\displaystyle t={\frac {{\overline {x}}-{\overline {y}}-\omega _{0}}{s}}}$ with , , , , and . ${\displaystyle {\overline {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}}$ ${\displaystyle {\overline {y}}={\frac {1}{m}}\sum _{i=1}^{m}y_{i}}$ ${\displaystyle s_{x}^{2}={\frac {1}{n-1}}\sum _{i=1}^{n}(x_{i}-{\overline {x}})^{2}}$ ${\displaystyle s_{y}^{2}={\frac {1}{m-1}}\sum _{j=1}^{m}(y_{j}-{\overline {y}})^{2}}$ ${\displaystyle s={\sqrt {{\frac {s_{x}^{2}}{n}}+{\frac {s_{y}^{2}}{m}}}}}$ ${\displaystyle \nu ={\frac {\left({\frac {s_{x}^{2}}{n}}+{\frac {s_{y}^{2}}{m}}\right)^{2}}{{\frac {\left({\frac {s_{x}^{2}}{n}}\right)^{2}}{n-1}}+{\frac {\left({\frac {s_{y}^{2}}{m}}\right)^{2}}{m-1}}}}}$
Rejection area ${\displaystyle H_{0}}$	${\displaystyle \{t|t>t_{1-\alpha ;\nu }\}\,}$	${\displaystyle \{t|t<-t_{1-\alpha /2;\nu }\}\,}$ or ${\displaystyle \{t|t>t_{1-\alpha /2;\nu }\}\,}$	${\displaystyle \{t|t<-t_{1-\alpha ;\nu }\}\,}$

Alternative tests

As stated above, the t-test is used to test hypotheses about expected values ​​of one or two samples from normally distributed populations with an unknown standard deviation.

• The assumption that each of the two groups is normally distributed can be tested with the Shapiro-Wilk test or the Kolmogorow-Smirnow test . If there is no normal distribution, nonparametric tests can be used as a substitute for the t-test , such as a Wilcoxon-Mann-Whitney test (also: Wilcoxon rank sum test) for independent samples or a Wilcoxon signed rank test for paired samples. A simple alternative method for rapid assessment is the Tukey rapid test .
• If more than two normally distributed samples are to be tested for equality of the expected values, an analysis of variance can be used.
• Gaussian tests can be used when comparing the mean values ​​of normally distributed samples with known standard deviation .

Web links

• Calculator for all variants of the t-test. Calculates t-value, p-value and critical values.

Individual evidence

1. ^ Jürgen Bortz: Statistics for human and social scientists . 6th edition, Springer, Berlin 2005, ISBN 3-540-21271-X , p. 142.
2. ^ RR Wilcox: Statistics for the Social Sciences . Academic Press Inc, 1996, ISBN 0-12-751540-2 .
3. ^ DG Bonnet, RM Price: Statistical inference for a linear function of medians: Confidence intervals, hypothesis testing, and sample size requirements . In: Psychological Methods . tape 7 , no. 3 , 2002, doi : 10.1037 / 1082-989X.7.3.370 .