Errors 1st and 2nd kind
The 1st and 2nd type errors , also called α errors (alpha errors) and β errors (beta errors), denote a statistical mistake. They refer to a method of mathematical statistics, the so-called hypothesis test . When testing a hypothesis, there is a Type I error if the null hypothesis is rejected when it is actually true (based on a randomly increased or decreased number of positive results). On the other hand, a type 2 error means that the test erroneously does not reject the null hypothesis , although the alternative hypothesis is correct. Errors of the 1st and 2nd type are often mentioned in the statistical quality control (see inspection lot ) as producer risk and consumer risk. In process control by means of quality control cards, the terms blind alarm and omitted alarm are used for this . Type 1 and 2 errors are also known as frequentist concepts . Nevertheless, type 1 and type 2 errors are always conditional probabilities . The concept of type 1 and 2 errors was introduced by Neyman and Pearson.
Decision table
| reality | |||
|---|---|---|---|
| H 0 is true | H 1 is true | ||
| Decision of the test ... |
... for H 0 | Correct decision (specificity) Probability: 1 - α |
Type 2 error probability: β |
| ... for H 1 |
Type 1 error Probability: α |
correct decision probability: 1-β ( selectivity of the test , sensitivity) |
|
Formal representation
A statistical test is a decision problem that involves an unknown parameter that must be in a certain parameter space . The parameter space can be broken down into two disjoint subsets and . The decision problem now lies in deciding whether lies in or . Identify the null hypothesis and the alternative hypothesis . Because and are disjoint, only one of the two hypotheses can be true. Since a hypothetical test always implies a decision, there is a likelihood that one will make a wrong decision. Be and . Once the rejection range and test statistic have been defined, then the probability of rejecting each can be determined. Let , where it is rejected if the test statistic falls in the critical range ( ). The function is also called a quality function . Usually there is a different probability of rejecting the null hypothesis , even if it is true (called type I error). In hypothesis testing, it is common to design test procedures only so that this probability is limited by a constant called the significance level of the test. That is, the significance level is the greatest value of for each value of which makes true, that is . In contrast to the 1st type error, the 2nd type error is not controlled by a specified limit . It's I. A. not possible to minimize both error probabilities at the same time. Therefore, among all the significance tests (tests that check for an error of type I), the one that minimizes the probability of error is sought. In other words: If the level of significance or the type 1 error has been determined a priori , then one is interested in maximizing the degree of discrimination against all relevant alternatives. The selectivity of a test is 1 minus the probability of making a type 2 error, i.e. H. . The probability of a type 2 error is not considered to be predetermined, but rather to be dependent on the parameter present in the population. In summary, the following applies to the probability of making a type 1 or type 2 error
- and .
In the case of “simple” hypotheses (such as, for example, vs. ), only the equals sign applies to the probability of committing a type 1 error. H. . In general, a decrease in increases the likelihood of type 2 errors and vice versa. Through complicated calculations can also be determined.
Type 1 error
There is a Type I error in testing a hypothesis if the null hypothesis is rejected when it is actually true (based on false positives ).
The initial hypothesis (null hypothesis) is the assumption that the test situation is in the "normal state". If this "normal state" is not recognized, although it actually exists, a type 1 error results. Examples of a type 1 error are:
- the patient is seen as sick even though he is actually healthy (null hypothesis: the patient is healthy ),
- the defendant is convicted of being guilty when in reality he is innocent (null hypothesis: the defendant is innocent ),
- the person is not granted access although they have access authorization (null hypothesis: the person has access authorization )
The level of significance or probability of error is the maximum probability , determined before a hypothesis test, that the null hypothesis will be rejected on the basis of the test results even though the null hypothesis is true. As a rule, one chooses a significance level of 5% (significant) or 1% (very significant).
The other possible wrong decision, namely to reject the alternative hypothesis even though it is true, is called Type II error.
Examples
- A tester has an urn in front of him that he cannot look into. There are red and green balls inside. Only one ball can be removed from the urn for testing purposes.
Alternative hypothesis: "There are more red balls than green balls in the urn".
In order to be able to give a judgment about the contents of the urn, the tester will remove balls from the urn several times for test purposes. If he then comes to the decision that the alternative hypothesis may be correct, i.e. he is of the opinion that there are more red than green balls in the urn, although in reality the null hypothesis is correct, namely that as many red as green or fewer red than If there are green balls in the urn, he is committing a type I error. - We want to check whether a new learning method increases the learning performance of students. To do this, we compare a group of students who were taught using the new learning method with a sample of students who were taught using the old method.
Alternative hypothesis: “Students who were taught according to the new learning method have a higher learning performance than students who were taught according to the old method.”
Assuming in our study, the sample of students who were taught according to the new learning method actually shows a better one Learning performance on. Perhaps this difference is due to coincidence or other influences. If, in truth, there is no difference at all between the two populations and we erroneously reject the null hypothesis - that is to say, consider it certain that the new method improves learning - then we are making a mistake of type I. This can of course have fatal consequences if we z. For example, converting the entire teaching to the new learning method with high costs and effort, even though this does not actually produce any better results. - Spam filter for incoming e-mails : A filter should recognize whether an e-mail is spam or not.
Null hypothesis: It is normal e-mail and not spam.
Alternative hypothesis: It's spam.
If an e-mail is classified as spam, but in reality it is not spam, i.e. the e-mail is incorrectly classified as spam, we speak of an error type I (false-positive).
Type 2 error
In contrast to the 1st type error, a 2nd type error means that the test incorrectly confirms the null hypothesis even though the alternative hypothesis is correct.
Difficulties in determining the error Art
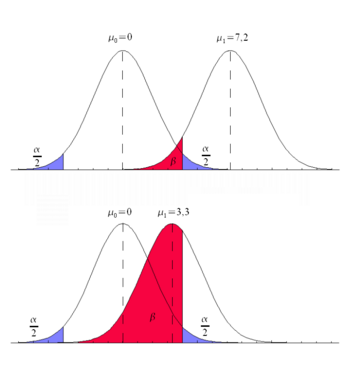
In contrast to the 1st type risk of mistakenly rejecting the given null hypothesis, although it actually applies, the 2nd type risk, i.e. the probability of a 2nd type error, can usually not be determined in advance. The reason for this is the way in which the hypotheses of statistical tests are determined: While the null hypothesis always represents a specific statement such as, for example , “mean value” , the alternative hypothesis is because it basically covers all other possibilities so that i. d. Usually only of a rather indeterminate or global nature (for example : “mean value ”).
The graphic on the right illustrates this dependency of the probability of a type 2 error ; (red) from the unknown mean value , if the “significance level”, i.e. H. type 1 maximum risk ; (blue) the same value is selected in both cases. As can be seen, there is also the paradoxical situation that the probability of an error of type 2, the greater the closer the true value is to the value asserted by the null hypothesis , up to the point that for the risk of type 2 ; the limit value ; accepts. In other words, the smaller the deviation of the actual value from the claimed value , the paradoxically greater the probability of making a mistake if one continues to believe the claimed value based on the test result (although the difference between the two values may be practically irrelevant due to their insignificance more plays). As this contradiction shows, dealing with the problem of type 2 errors in a purely formal-logical manner can easily be the basis for wrong decisions. In biometric and medical statistical applications, the probability of making a decision for H 0 if H 0 is correct is called specificity . The probability of making a decision for H 1 if H 1 is correct is called the sensitivity . It is desirable for a test method to have high sensitivity and high specificity and thus low probabilities for the errors of the first and second type.
Examples
- In Six Sigma project management: Type 1 error: At the end of the project, you notice that aspects were left out during the initial planning (“too little done”). A type 2 mistake here would be that the entire project was done about things that ultimately turn out to be superfluous or irrelevant for the success of the project (“done too much”).
- A tester has an urn in front of him that he cannot look into. There are red and green balls inside. Only one ball can be removed from the urn for testing purposes.
- Alternative hypothesis : "There are more red balls than green balls in the urn".
- In order to be able to give a judgment about the contents of the urn, the tester will remove balls from the urn several times for test purposes. The null hypothesis in our example is that there are either as many red balls as green balls or more green balls than red balls in the urn (the opposite of the alternative hypothesis ). If, based on his sample, the tester comes to the conclusion that the null hypothesis is correct or the alternative hypothesis is incorrect, although in truth the alternative hypothesis is correct, then he is making a type 2 error.
- We would like to examine the influence of diet on the mental development of children in children's homes. To do this, we compare two groups of children with regard to their performance in cognitive tests: One sample is fed according to the conventional plan, the other receives a particularly healthy diet. We suspect that the healthy diet has a positive effect on cognitive performance.
- Alternative hypothesis: "Children who receive a particularly healthy diet have better cognitive performance than children who are fed the conventional way."
- If we now compare the cognitive performance of our two samples, we find no difference in cognitive performance. As a result, we consider the alternative hypothesis to be false and confirm the null hypothesis. However, if the truth is that the healthy nourished population is performing better, then we are making a Type II error.
- But did we not find a difference in our sample? This equality can, however, also be due to the random scattering of the measurement results or to the unfavorable composition of our samples.
- Committing a type 2 error is usually less “bad” than a type 1 error. However, this depends individually on the subject of the investigation. In our example, the Type II mistake has very negative consequences: Although a healthy diet improves performance, we decide to stick to the conventional diet. A mistake of the first kind, i.e. the introduction of a healthy diet for all children, although this does not lead to an improvement in performance, would have had fewer negative consequences here.
Opposite notation
In some sources, the exact opposite notation is used for type 2 error and test severity. There the probability of committing a type 2 error is denoted by the value 1-β, while the test strength or power is denoted by β.
Agnostic Tests
In May 2018, Victor Coscrato , Rafael Izbicki and Rafael Bassi proposed a method with which both type 1 and type 2 errors can be controlled. They call such a procedure "agnostic test". In addition to the 1st and 2nd type errors, a further so-called 3rd type error is defined in agnostic tests. This occurs when the result of the test neither supports the null hypothesis ( ) nor the alternative hypothesis ( ) , but rather its result remains agnostic.
See also
Web links
Individual evidence
- ↑ a b Denes Szucs, John Ioannidis : When Null Hypothesis Significance Testing Is Unsuitable for Research: A Reassessment. In: Frontiers in human neuroscience. Volume 11, 2017, p. 390, doi: 10.3389 / fnhum.2017.00390 , PMID 28824397 , PMC 5540883 (free full text) (review).
- ↑ Philip Sibbertsen and Hartmut rest: Statistics: Introduction for economists and social scientists. , P. 379
- ^ Ludwig Fahrmeir , Rita artist, Iris Pigeot , Gerhard Tutz : Statistics. The way to data analysis. 8., revised. and additional edition. Springer Spectrum, Berlin / Heidelberg 2016, ISBN 978-3-662-50371-3 , p. 385.
- ↑ Bayer, Hackel: Probability Calculation and Mathematical Statistics , p. 154
- ↑ Note : Both beta (and alpha) represent conditional probabilities
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee. Introduction to the Theory and Practice of Econometrics. 2nd Edition. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore 1988, ISBN 0-471-62414-4 , p. 96 ff
- ↑ Jeffrey Marc Wooldridge : Introductory econometrics: A modern approach. 4th edition. Nelson Education, 2015, p. 779.
- ↑ George G. Judge, R. Carter Hill, W. Griffiths, Helmut Lütkepohl , TC Lee. Introduction to the Theory and Practice of Econometrics. 2nd Edition. John Wiley & Sons, New York / Chichester / Brisbane / Toronto / Singapore 1988, ISBN 0-471-62414-4 , p. 96 ff
- ↑ James L. Johnson: Probability and Statistics for Computer Science. , P. 340 ff
- ↑ Erwin Kreyszig: Statistical methods and their applications ; 7th edition, Göttingen 1998, pp. 209ff.
- ↑ Victor Coscrato, Rafael Izbicki, Rafael Bassi Stern: Agnostic tests can control the type I and type II errors simultaneously . In: arXiv: 1805.04620 [math, stat] . May 11, 2018, arxiv : 1805.04620 .
































