Five lemma

The five-lemma is an important lemma about commutative diagrams , which is frequently used in mathematics , mainly in homological algebra and other applications of Abelian categories .

The five lemma is not only valid in Abelian categories, but also, for example, in the category of groups. It is obtained by combining the two four-lemmas that form dual statements.

statement

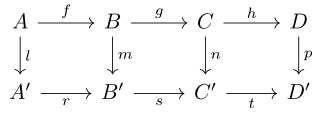
Consider the following commutative diagram in any Abelian category (such as the category of vector spaces over a given field or the category of Abelian groups):

Let the lines be exact , and be isomorphisms , an epimorphism , a monomorphism . The five lemma says that there is also an isomorphism. ${\ displaystyle m}$ ${\ displaystyle p}$ ${\ displaystyle l}$ ${\ displaystyle q}$ ${\ displaystyle n}$

The (first) four lemma says: Are in the commutative diagram

the lines are exact, and epimorphisms and a monomorphism, so is an epimorphism. ${\ displaystyle m}$ ${\ displaystyle p}$ ${\ displaystyle q}$ ${\ displaystyle n}$

The (second) four lemma says: Are in the commutative diagram

the lines exactly, and monomorphisms and an epimorphism, so is a monomorphism. ${\ displaystyle m}$ ${\ displaystyle p}$ ${\ displaystyle l}$ ${\ displaystyle n}$

proof

The proof is provided by chart hunt , detailed below in the category of groups (the neutral element is denoted by 1, the link is written as multiplication). It is (translated into additive notation) directly transferable to the category of the Abelian groups or the modules above a ring and thus applies to all Abelian categories according to Mitchell's embedding theorem .

For the proof of the first four lemma, let in

the lines exactly, and surjective and injective . We have to show that is surjective. ${\ displaystyle m}$ ${\ displaystyle p}$ ${\ displaystyle q}$ ${\ displaystyle n}$

So be any element of . ${\ displaystyle c '}$ ${\ displaystyle C '}$

Since is surjective, there is an in with . ${\ displaystyle p}$ ${\ displaystyle d}$ ${\ displaystyle D}$ ${\ displaystyle p (d) = t (c ')}$

Because of the commutativity of the diagram is . ${\ displaystyle q {\ bigl (} j (d) {\ bigr)} = u {\ bigl (} p (d) {\ bigr)}}$

Because of the accuracy , so . ${\ displaystyle u {\ bigl (} t (c ') {\ bigr)} = 0}$ ${\ displaystyle q {\ bigl (} j (d) {\ bigr)} = 0}$

Because of the injectivity of, it follows from this . ${\ displaystyle q}$ ${\ displaystyle j (d) = 0}$

Since it lies in the core of , it lies in the image of , i.e. H. there is an off with . ${\ displaystyle d}$ ${\ displaystyle j}$ ${\ displaystyle h}$ ${\ displaystyle c}$ ${\ displaystyle C}$ ${\ displaystyle h (c) = d}$

Then applies . ${\ displaystyle t {\ bigl (} n (c) {\ bigr)} = p {\ bigl (} h (c) {\ bigr)} = p (d) = t (c ')}$

Hence, for on is off . ${\ displaystyle c '= x \ cdot n (c)}$ ${\ displaystyle x}$ ${\ displaystyle \ ker (t) = im (s)}$

So be an element of with . ${\ displaystyle b '}$ ${\ displaystyle B '}$ ${\ displaystyle s (b ') = x}$

Since is surjective, there is an in with . ${\ displaystyle m}$ ${\ displaystyle b}$ ${\ displaystyle B}$ ${\ displaystyle m (b) = b '}$

It follows

{\ displaystyle {\ begin {aligned} n {\ bigl (} g (b) \ cdot c {\ bigr)} & = n {\ bigl (} g (b) {\ bigr)} \ cdot n (c) = s {\ bigl (} m (b) {\ bigr)} \ cdot n (c) \\ & = s (b ') \ cdot n (c) = x \ cdot n (c) = c'. \ end {aligned}}}

Thus it is indeed surjective. ${\ displaystyle n}$

The second four lemma is dual to the first or can be proved in the same simple way.

The five-lemma then follows immediately by combining the two four-lemma.

Short five lemma

Are in the commuting diagram

the lines are short exact sequences and and isomorphisms, so is an isomorphism. ${\ displaystyle g}$ ${\ displaystyle h}$ ${\ displaystyle f}$

This follows immediately (again for Abelian categories or the category of groups) from the five lemma, since one can add the zero mapping between the zero objects .

With the short five-part lemma in particular, a common mistake is to infer the isomorphism of and as soon as one finds isomorphisms and . However, this is a fallacy, because the lemma does not claim the existence of an isomorphism, as long as you do not do at least one to and matching homomorphism has. ${\ displaystyle B}$ ${\ displaystyle B '}$ ${\ displaystyle g}$ ${\ displaystyle h}$ ${\ displaystyle g}$ ${\ displaystyle h}$ ${\ displaystyle f}$

Applications

The five lemma is often applied to long exact sequences: To calculate the homology or cohomology of a given object, one typically uses a simpler sub-object with known (co-) homology. This provides a long, exact sequence in which the homology groups sought appear. Admittedly, this alone is normally not sufficient to determine the homology groups; but if one can compare the original object and its sub-object with known objects using morphisms, a homomorphism is induced between long exact sequences and the five-lemma can then determine the unknown groups.

Web links

Margherita Barile: Five Lemma . In: MathWorld (English).