Snake lemma

The snake lemma , a statement from the mathematical subfield of homological algebra that is valid in all Abelian categories , is a tool for the construction of the long exact sequences considered there . It has important applications, for example, in algebraic topology . The homomorphisms constructed with the snake lemma are commonly referred to as compound homomorphisms .

statement

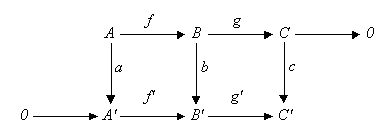
In an Abelian category (e.g. the category of the Abelian groups or the vector spaces over a given body ) the following commutative diagram is given:

Let the lines be exact and denote the zero object . Then there is an exact sequence comprising the cores and cokernels of , , set in relation: ${\displaystyle 0}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

${\displaystyle \ker a\;{\color {Gray}\longrightarrow }\ker b\;{\color {Gray}\longrightarrow }\ker c\;{\overset {d}{\longrightarrow }}\operatorname {coker} a\;{\color {Gray}\longrightarrow }\operatorname {coker} b\;{\color {Gray}\longrightarrow }\operatorname {coker} c}$

If there is also a monomorphism , so is the morphism . If there is an epimorphism , this also applies to . ${\displaystyle f}$ ${\displaystyle \ker a\to \ker b}$ ${\displaystyle g'}$ ${\displaystyle \operatorname {coker} b\to \operatorname {coker} c}$

In the category of groups , however, the snake lemma is applicable only if additional conditions to the homomorphisms , , (see below). ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$

origin of the name

If you expand the diagram to include cores and coke cores, you can see how the claimed exact sequence "snakes" through the diagram:

proof

For the proof one first assumes that the diagram concerns the category of modules over a ring . This allows the claim to be proven by chart hunting. The validity for the case of any Abelian category then results from Mitchell's embedding theorem .

Construction of the homomorphisms

The homomorphisms between the cores or coke nuclei are naturally induced by the given horizontal homomorphisms via the universal properties of the core or coke core. The essential message of the lemma is the existence of the connection homomorphism that completes the sequence. ${\displaystyle d}$

In the case of the category of Abelian groups or of modules over a ring, one can construct element-wise by means of diagram hunting: Let be given, i.e. H. a with . Because of the surjectivity of there is a with . Because there is a (because of the injectivity of unique) with . Define as the image of in . ${\displaystyle d}$ ${\displaystyle x\in \operatorname {ker} \,c}$ ${\displaystyle x\in C}$ ${\displaystyle c(x)=0}$ ${\displaystyle g}$ ${\displaystyle y\in B}$ ${\displaystyle g(y)=x}$ ${\displaystyle g'(b(y))=c(g(y))=0}$ ${\displaystyle f'}$ ${\displaystyle z\in A'}$ ${\displaystyle f'(z)=b(y)}$ ${\displaystyle d(x)}$ ${\displaystyle z}$ ${\displaystyle \operatorname {coker} \,a}$

The choice of was not clear here, but due to the accuracy of every other choice has the shape for the appropriate one . As a result, is replaced by , which then leads to the same value for . Thus the mapping is well defined. ${\displaystyle y\in B}$ ${\displaystyle B}$ ${\displaystyle y+f(w)}$ ${\displaystyle w\in A}$ ${\displaystyle z}$ ${\displaystyle z+a(w)}$ ${\displaystyle d(x)}$ ${\displaystyle d}$

If you have chosen to and with and , you can choose to obviously as well : , . From this it follows . Likewise, if is a ring element, it follows from and that is. The mapping is therefore linear, i.e. a homomorphism. ${\displaystyle x_{1},x_{2}\in \operatorname {ker} (c)}$ ${\displaystyle y_{1},y_{2}\in B}$ ${\displaystyle z_{1},z_{2}\in A'}$ ${\displaystyle g(y_{1,2})=x_{1,2}}$ ${\displaystyle f'(z_{1,2})=b(y_{1,2})}$ ${\displaystyle x_{1}+x_{2}}$ ${\displaystyle y_{1}+y_{2}}$ ${\displaystyle z_{1}+z_{2}}$ ${\displaystyle g(y_{1}+y_{2})=x_{1}+x_{2}}$ ${\displaystyle f'(z_{1}+z_{2})=b(y_{1}+y_{2})}$ ${\displaystyle d(x_{1}+x_{2})=d(x_{1})+d(x_{2})}$ ${\displaystyle r}$ ${\displaystyle g(r\cdot y_{1})=r\cdot x_{1}}$ ${\displaystyle f'(r\cdot z_{1})=b(r\cdot y_{1})}$ ${\displaystyle d(r\cdot x_{1})=r\cdot d(x_{1})}$ ${\displaystyle d}$

Complex property

It follows quickly that the snake sequence forms a complex, i.e. that two "arrows" in a row always result in the zero mapping :

• The imaging is induced by ${\displaystyle \ker a\to \ker c}$ ${\displaystyle g\circ f=0}$
• For the illustration be and . Then you can from in the above construction of this very select, from which , then and thus yields. ${\displaystyle \ker b\to \operatorname {coker} a}$ ${\displaystyle y\in \ker b}$ ${\displaystyle x=g(y)}$ ${\displaystyle d(x)}$ ${\displaystyle y}$ ${\displaystyle b(y)=0}$ ${\displaystyle z=0}$ ${\displaystyle d(x)=0}$
• For the illustration let . With the designations as in the construction above, the picture in results from . Since this is in , the result is 0. ${\displaystyle \ker c\to \operatorname {coker} b}$ ${\displaystyle x\in \ker c}$ ${\displaystyle \operatorname {coker} b}$ ${\displaystyle b(y)\in B'}$ ${\displaystyle \operatorname {Bild} b}$
• The imaging is induced by ${\displaystyle \operatorname {coker} a\to \operatorname {coker} c}$ ${\displaystyle g'\circ f'=0}$

accuracy

The exactness of the homomorphisms between the nuclei, between the coke nuclei and at the beginning and end of the arrow d can in turn be demonstrated by hunting a diagram:

• Accuracy at : Is with , so at least for one . Because of and the injectivity of follows , so in fact as required for one . ${\displaystyle \ker b}$ ${\displaystyle x\in \ker b}$ ${\displaystyle g(x)=0}$ ${\displaystyle x=f(u)}$ ${\displaystyle u\in A}$ ${\displaystyle f'(a(u))=b(f(u))=b(x)=0}$ ${\displaystyle f'}$ ${\displaystyle a(u)=0}$ ${\displaystyle x=f(u)}$ ${\displaystyle u\in \ker a}$
• Accuracy at : Be with us . With the designations above is then for a . Then , hence, for one . So that ${\displaystyle \ker c}$ ${\displaystyle x\in \ker c}$ ${\displaystyle d(x)=0}$ ${\displaystyle z=a(u)}$ ${\displaystyle u\in A}$ ${\displaystyle b(y)=f'(z)=f'(a(u))=b(f(u))}$ ${\displaystyle y=f(u)+v}$ ${\displaystyle v\in \ker b}$ ${\displaystyle x=g(y)=g(f(u))+g(v)=g(v)}$
• Accuracy at : An element of always comes from one . That it is mapped on means that it is in the picture of . Be with us and bet . Then applies . Thus it is and will be mapped to the given as it is after construction . ${\displaystyle \operatorname {coker} a}$ ${\displaystyle {\bar {z}}}$ ${\displaystyle \operatorname {coker} a}$ ${\displaystyle z\in A'}$ ${\displaystyle 0\in \operatorname {coker} b}$ ${\displaystyle f'(z)}$ ${\displaystyle b}$ ${\displaystyle y\in B}$ ${\displaystyle b(y)=f'(z)}$ ${\displaystyle x=g(y)}$ ${\displaystyle c(x)=c(g(y))=g'(b(y))=g'(f'(z))=0}$ ${\displaystyle x\in \ker c}$ ${\displaystyle {\bar {z}}}$
• Exactness at : If the image is from and is mapped to the zero in , then applies to a . Because of the surjectivity of there is a with . Then , so for one . In the transition to the Kokernen falls away, so is the image of . ${\displaystyle \operatorname {coker} b}$ ${\displaystyle {\bar {x}}\in \operatorname {coker} b}$ ${\displaystyle x\in B'}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle \operatorname {coker} c}$ ${\displaystyle g'(x)=c(y)}$ ${\displaystyle y\in C}$ ${\displaystyle g}$ ${\displaystyle z\in B}$ ${\displaystyle g(z)=y}$ ${\displaystyle g'(b(z))=c(g(z))=c(y)=g'(x)}$ ${\displaystyle x=b(z)+f'(u)}$ ${\displaystyle u\in A'}$ ${\displaystyle b(z)}$ ${\displaystyle {\bar {x}}}$ ${\displaystyle {\bar {u}}\in \operatorname {coker} a}$

The last three points take advantage of the fact that the vertical sequences are exact.

naturalness

For applications of the snake lemma it is often necessary that the long exact sequences are "natural" (in the sense of a natural transformation ). This then results from the naturalness of the sequence delivered by the snake lemma.

Is

a commutative diagram with exact lines, the snake lemma can be applied once to the "front" part and once to the "back" part. The two resulting exact sequences are linked to one another via a diagram of the shape

in relationship.

This can also be seen by applying the snake lemma to the category of morphisms between objects of the original category.

Category of groups

Since a number of theorems of homological algebra are valid not only for Abelian categories but also for the category of groups, it should be pointed out that this is not the case for the snake lemma. A natural connection homomorphism d can also be found here , but the long sequence is only a chain complex and not necessarily exact. Only if the vertical sequences are exact, i.e. H. the pictures under a , b and c are each normal divisors in A , B and C , the proof of the exactness also works for groups.

The simple alternating group contains a subgroup that is isomorphic to the symmetric group , in which the cyclic group in turn is a normal divisor . A commutative diagram is obtained from this ${\displaystyle A_{5}}$ ${\displaystyle S_{3}}$ ${\displaystyle C_{3}}$

${\displaystyle {\begin{matrix}&0&\to &C_{3}&\to &C_{3}&\to 0\\&\downarrow &&\downarrow &&\downarrow \\0\to &0&\to &S_{3}&\to &A_{5}\end{matrix}}}$

with exact lines.

Since is simple, the coke core of the right figure is trivial, while isomorphic to . The long sequence therefore has the form ${\displaystyle A_{5}}$ ${\displaystyle S_{3}/C_{3}}$ ${\displaystyle C_{2}}$

${\displaystyle 0\longrightarrow 0\longrightarrow 0\longrightarrow 0\longrightarrow C_{2}\longrightarrow 0}$

and is therefore not exact.

useful information

• In the film It's My Turn ( 1980 ) Jill Clayburgh proves the snake lemma.
• Charles A. Weibel in his book "An Introduction to Homological Algebra" (Cambridge U. Press, 1994) dispenses with a proof with reference to It's My Turn .
• At the very beginning of the film The Graduation Examination ( 1967 ) you can see the statement of the snake lemma on a board behind Dustin Hoffman .

literature

• MF Atiyah , IG Macdonald : Introduction to Commutative Algebra . Oxford 1969, Addison-Wesley Publishing Company, Inc. ISBN 0-201-00361-9 .
• Peter Hilton , Urs Stammbach : A course in homological algebra. 2nd edition, Springer Verlag, Graduate Texts in Mathematics, 1997, ISBN 0-387-94823-6 .