Eclipse cycle
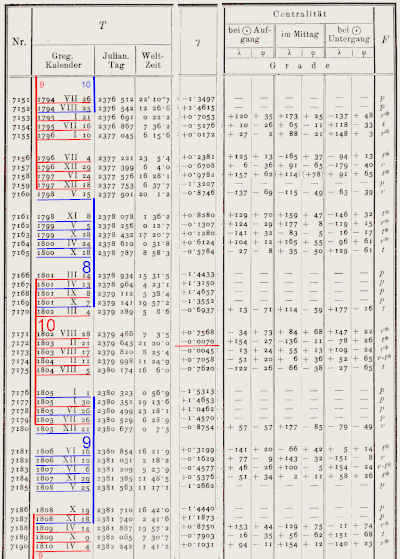
(excerpt from a reproduction of Theodor Oppolzer's calculations , 1887)
The various series of the semester cycle are highlighted in color ; they usually overlap for a short time and each consist of 8, 9 or 10 events.
An eclipse cycle is the periodic repetition of either solar eclipses or lunar eclipses . From the sequence of all eclipses ( Canon of the eclipses ) different types of eclipse cycles can be read out, which are differentiated by the time interval between the individually allocated eclipses - the eclipse period :
- so has z. B. the semester cycle with 6 synodic months (about half a year) the shortest eclipse period
- in contrast, the Saros cycle has a period of 223 lunations (about 18 years).
Overlapping rows of eclipses
A cycle of eclipses is not a continuous sequence of eclipses, but consists of series of eclipses , which are limited in the number of events and offset in time from one another. The first eclipses of a series are weak ( partial ), the ones in the middle are clear ( total ), and the last are weak again, before no eclipse of the series under consideration can be determined after the characteristic period.
The series of the semester cycle contain 8 to 10 events (see table on the right). Before a series ends after a maximum of 5 years, new events usually take place with which a new semester series begins, i. H. both rows overlap.
Eclipse cycles with longer periods are also longer because of the larger number of events they contain, which also differ less from one another, and more series with more pronounced temporal overlap exist in parallel. A Saros series contains e.g. B. about 71 events and lasts about 1270 years, about 38 Saros series exist at the same time.
Labelling
Both the superordinate term, which only refers to the eclipse period, and each eclipse series is referred to as an eclipse cycle. Confusion cannot therefore be ruled out.
In the case of cycles with a long period, this is countered by each of their individual rows having its own number. The solar eclipse of August 11, 1999 was one of B. in the series with No. 145, in short: to the Saros cycle 145.
Cycle readout
The principle of forming a cycle type for reading out certain series of solar eclipses is the same as for lunar eclipses. In the following sections, the cycles are first treated generally or as solar eclipse cycles. Special features of lunar eclipse cycles will be discussed later.
The next eclipse can occur after one lunation (about a month). An eclipse series, however, is one made up of more than two events. Their period is at least six lunations (about half a year), which characterize the semester cycle. An eclipse after a lunation usually takes place before a semester series ends. With this event, the next series of eclipses in the semester cycle begins.
The period of a readout cycle is an integral multiple of synodic months. With an increasing eclipse period, each series also contains a higher number of eclipse events, all of which are related to one another with the same period without interruption. As the period increases, the respective difference to an integer multiple of half a draconian months becomes smaller and smaller, that is, the change in the node distance between the individual events becomes smaller and the events therefore become more similar to one another. The larger the eclipse period, the more such long series with the same period run parallel to each other.
The number of skipped eclipses increases with the eclipse period. The selection condition is that the period contains a whole number of synodic months as well as a whole number of half draconian months. Since eclipses can occur when the moon is close to either node , the condition also applies to an integer number of draconian months plus half a month. In such cycles, the eclipses take place one after the other, alternating near the ascending or descending node. Suitable pairs of numbers of synodic and drakonitischen months, with continued fraction finding calculations.
A cycle series can begin with any darkness. For this reason, there are just as many additional series of a cycle type of a certain period at the same time as an eclipse series as events with the relevant readout mode were skipped. The Saros currently has 38 more rows, each with a different number. In principle, every eclipse can be recorded by any type of cycle and then related to other eclipses with period lengths that are differently determined depending on the type. Readout cycles can be of any size. In theory there is no limit.
The two following figures show, for example, the result of such a selection in the Saros cycle - and in comparison to the semester cycle.

The previous series ended with eclipse v e , the next one begins with n a .

sake of clarity, only even-numbered eclipses are marked.
Saros cycle
The number of eclipses contained in a series increases proportionally with the period, but the duration of a series grows disproportionately and soon exceeds a human life significantly. Among the larger cycle types, the Saros cycle (period 223 synodic months, about 18.03 years; series with an average of 71 eclipses distributed over about 1280 years) is of particular practical importance, although an observer can only experience five to six eclipses in this cycle. An astronomer with an average life expectancy in ancient times could observe at least three of them and evaluate them scientifically. Three Saros periods are in turn the period of the Exeligmos ( Triple Saros ).
It is essential for the meaning of the Saros cycle that the similarity of the successive eclipses is not only determined by the relatively small change in the node distance, but that the Saros period is also almost an integral multiple of an anomalous month , i.e. the moon is more similar Distance to the earth.
Other cycle types
Between semester *) and Saros there are the cycle types Hepton *) (synodic months), Octon (47), Anonymos *) (88) and Tritos *) (135) depending on their period length .
The Saros is followed by the very large Inex cycle *). Its period is 358 synodic months. An inex series contains an average of 809 solar eclipses distributed over 23,400 years. The node distance is only 0.041 °.
Cycles with relatively long periods, which were already known in ancient times, are, for example, a cycle type of the Maya (405 synodic months equals 3 Tritos periods equals about 33 years equals 46 Tzolkin periods of 260 days each) and one of the Greeks (939 synodic months equals about 4 metons) -Periods equal to 20 octons -periods equal to about 76 years).
Note: in the cycles marked with *) , the eclipses take place one after the other alternately near the ascending or descending node.
Assumptions and accuracy
For the earth as a whole, under certain conditions, a lunar eclipse can occur almost 15 days before or after a solar eclipse; this lasts half a lunation between two eclipses For the reproduction of the connections, the simplifying assumption here is circular instead of elliptical orbits of the earth and of the moon as well as average values for their orbital times. The specified values for period, number of eclipses and duration of a cycle series are thus also mean values that are sufficient for the abstraction of the periodicity of cycle types, but not for detailed calculations of an eclipse. The auxiliary variables node distance (as ecliptical angular distance between the new or full moon and the node) and eclipse limit (as the maximum node distance up to which an eclipse can arise) are given as mean values.
These theoretical mean values are compared with statistical mean values. The latter fluctuate depending on the eclipses evaluated in a statistic, which must be taken into account when using values taken from the literature. Since every new eclipse never completely resembles an older one, working with mean values is not free of a residue of arbitrariness anyway.
Some calculations
Predefined sizes
During a synodic month ( 29.53059 days ) the earth moves + 29.1067 ° on its orbit (360 ° in 365.2422 days ), the nodal line rotates during this time −1.5638 ° in the ecliptic (360 ° in 18,613 years ):
- (29.53059 d ÷ 365.2422 d) 360 ° = 29.1067 °,
- (29.53059 d ÷ (18.613 365.2422 d)) 360 ° = 1.5638 °.
Node distance change in the semester cycle
After 6 synodic months the earth has advanced on its orbit + 174.6402 °, the nodal line has rotated −9.3828 °. The new or full moon has come + 4.0230 ° (change in node distance, ecliptical angle) beyond the opposite node:
- + 174.6402 ° - (−9.3828 °) - 180 ° = + 4.0230 °.
Eclipse number and cycle duration for the semester cycle (solar eclipses)
With the eclipse limit ± 16.6 ° (average value, see entry in this figure ), the eclipse number is 9.25 on average, the cycle duration on average 4.5 years:
- (2 16.6 ° ÷ 4.023 °) + 1 ≈ 9.25
(+1, because the number of interval limits = number of intervals + 1) - 9.25 · 6 · 29.53059 d ≈ 4.5 years.
Geographical aspect of solar eclipses
The first and last eclipses in a series are partial and take place in one of the two polar regions of the earth. In between they are central (total or ring-shaped) and gradually shift across all geographical latitudes until they stop in the opposite polar area. If the eclipses alternate between the ascending and descending nodes (*), the row consists of two nested sub-rows, one of which runs from south to north and the other from north to south.
If the value for the change in node distance is negative, the series of eclipses runs in a westerly direction in relation to the nodes. On Earth, their course between the polar regions is reversed to a series with a positive change in the nodal distance.
Total and circular total solar eclipses
The eclipses in the middle of a row are total or annular . Most of them are either total or ring-shaped, even if the period is approximately a whole multiple of the anomalous month (on average 27.55455 d). This condition is well met with the Hepton and the Saros :
- Hepton : 41 29.53059 d = 1210.7542 d ≈ 43.94 anomalous months,
- Saros : 223 29.53059 d = 6585.3216 d ≈ 238.99 anomalous months.
The Saros owes its goodness and fame to this property , very similar solar eclipses are repeated.
Cycle data in summary
| cycle |
synodic moons |
Earth years |
draconite moons |
anomalous moons |
Nodal distance change |
avg. Number of solar eclipses |
Years (total) |
|---|---|---|---|---|---|---|---|
| semester | 6th | 0.485 | 6.5112 (*) | + 4.023 ° | 9.25 | 4.0 | |
| Heptone | 41 | 3.31 | 44.4930 (*) | 43.94 | −2.509 ° | 14.2 | 43.7 |
| Octon | 47 | 3.80 | 51.0042 | + 1.514 ° | 22.9 | 83.2 | |
| Anonymous | 88 | 7.11 | 95.4972 (*) | −0.9772 ° | 35 | 241.7 | |
| Tritos | 135 | 10.92 | 146.5015 (*) | + 0.5181 ° | 65.1 | 700 | |
| Saros | 223 | 18.03 | 241,9987 | 238.99 | −0.4772 ° | 70.6 | 1,255 |
| Inex | 358 | 28.95 | 388.5001 (*) | + 0.0411 ° | 809 | 23,390 |
In the cycles marked with (*), the eclipses take place alternately one after the other in proximity to the ascending or descending node.
Multiples of periods of eclipse
The eclipse period known to the Maya of about 33 years is three times the Tritos period.
A whole-number extension of the Saros period leads to the Exeligmos or Triple Saros with a period duration of approximately 54 years (3 x 18.03 years). Its significance lies in the fact that an eclipse then takes place almost at the same time of day as another 54 years earlier, because 669 synodic months correspond to almost a whole number of days (669 · 29.53059 days = 19 755.965 days ≈ 19 756 days). The repetition of such eclipses can thus be observed from the same place, since the maximum of the eclipse is approximately at the same degree of longitude. This fact was already known in ancient Greece. The lunar circle , which is important for the formation of lunisolar calendars , shows a period of 235 synodic months, which is close to the five-fold period of the octon with 47 synodic months. Because of this coincidence, the lunar circle is often viewed as an eclipse cycle. Compared to Saros with a similar period length, it is an insignificantly short cycle with only four or five eclipses. If the octon period (which contains an average of 22.9 eclipses) is extended to five times, only every fifth eclipse is counted. The lunar circle thus includes only about half as many events as the otherwise shortest eclipse cycle, the semester .
The multiplication of the period reduces the number of eclipses in a cycle series by the same factor.
Lunar eclipse cycles
In contrast to the eclipses caused by the umbra of the earth, penumbral lunar eclipses are not easy to detect with the naked eye. In the Canon of Lunar Eclipses of Theodor Oppolzer they are therefore not listed (see right). The astronomical term, on the other hand, encompasses both types of lunar eclipse and therefore the events of a barely perceptible darkening of the moon by the penumbra of the earth are also included in more recent lists.
The eclipse limit including penumbral lunar eclipses is around ± 16.7 °, roughly the same as that for solar eclipses including partial solar eclipses (around ± 16.6 ° ). Cycles from lunar eclipses and those from solar eclipses are therefore about the same length and contain about the same number of events.
The eclipse limit is significantly smaller at around ± 10.6 ° and the time window is correspondingly narrower if the penumbral lunar eclipses are not counted. A lunar eclipse cycle series from the easily recognizable umbra eclipses thus contains only about two thirds of the events and is about one third shorter than a series in which the more difficult to recognize eclipses are also counted. For the semester cycle, for example, this leads to a reduction to 5 to 6 eclipses per row (see figure on the right), instead of the otherwise 8 to 10 lunar eclipses series (which can overlap in a similar way to the semester cycle for solar eclipses, see figure at the top).
Individual evidence
- ↑ a b c d Theodor Oppolzers : Canon of the darkness . Memoranda of the Imperial Academy of Sciences, mathematical and natural science class, Volume II, Vienna 1887 ( digitized version ).
- ^ Hermann Mucke, Jean Meeus: Canon of solar eclipses. Astronomical Office Vienna, 1992.
- ^ Hermann Mucke, Jean Meeus: Canon of the lunar eclipses. Astronomical Office Vienna, 1992.
- ^ Robert Harry van Gent: A Catalog of Eclipse Cycles
- ↑ Van den Bergh coined most of these names: Periodicity and variation of solar and lunar eclipses, Tjeenk Willink, Haarlem 1955.
- ↑ Van den Bergh (died 1966) developed this cycle, which is to be regarded as his main work (Periodicity and variation of solar and lunar eclipses, Tjeenk Willink, Haarlem 1955). He also chose its name.
- ↑ -180 °, because change to the opposite node
- ^ Jean Meeus, Hermann Mucke: Canon of Lunar Eclipses. Astronomical Office Vienna, 1979.
literature
- George van den Bergh: Periodicity and Variation of Solar and Lunar Eclipses. Tjeenk Willink, Haarlem 1955.
- Friedrich K. Ginzel: Special canon of solar and lunar eclipses for the country area of classical antiquity and the period from 900 BC to 600 AD. Mayer & Müller, Berlin 1899, digital copy of the SLUB Dresden via EOD
- Jean Meeus, Hermann Mucke: Canon of Lunar Eclipses. Astronomical Office Vienna, 1979.
- Theodor Oppolzers : Canon of the darkness. Memoranda of the Imperial Academy of Sciences, mathematical and natural science class, L II.Bd., Vienna 1887.
- JB Zirker: Total Eclipses of the Sun. Princeton University Press, 1995.
Web links
- Robert Harry van Gent: A Catalog of Eclipse Cycles. In: Webpages on the History of Astronomy. A Catalog of Eclipse Cycles. September 8, 2003, accessed October 4, 2008 (English, compilation of numerous cycles in the series of eclipses).
