Length contraction paradox

A paradox of length contraction arises when the reciprocal length contraction is considered without considering the relativity of simultaneity . This type of paradox is the counterpart of the twin paradox that arises from time dilation .

According to the special theory of relativity , a body resting in an inertial system is subject to the effect of length contraction from the point of view of inertial systems moving relative to it . Conversely, all bodies that rest in the second inertial system are also contracted from the perspective of the first inertial system. This leads to different variants of this paradox, with both kinematic and dynamic components playing a role. By considering the relativity of simultaneity, the problems can all be solved.

Garage paradox

Fig. 1

Fig. 2

A ladder and a garage move towards each other, with the ladder moving in the positive x direction from the garage's point of view . It should be assumed that the ladder is longer than the garage in the same state of motion, i.e. the rest length of the ladder is greater. But from the point of view of the inertial system in which the garage rests, the ladder is in motion, and because of the contraction in length, the ladder can be made so small that it fits into the garage by choosing a suitable speed (Fig. 1). In contrast, from the perspective of the ladder system, the garage is moved and consequently contracted. From this perspective the garage is smaller and the ladder cannot possibly fit in the garage (Fig. 2).

resolution

Fig. 3

Fig. 4

The fact that such situations do not lead to contradictions is due to the relativity of simultaneity , i.e. H. what an observer in the garage system perceives as being simultaneous is not simultaneously for an observer in the ladder system.

For this purpose, a garage with two gates (A = left, B = right, Fig. 3) is to be considered, which from the perspective of the garage system - i.e. measured with clocks resting in this system - open simultaneously before the ladder has penetrated (events A1 and B1), close at the same time when the ladder is completely enclosed (A2 and B2) and immediately open again to let the ladder through (A3 and B3). The sequence of events is A1 = B1 before A2 = B2 before A3 = B3.

On the other hand, from the perspective of the ladder system (FIG. 4), due to the relativity of simultaneity, the clocks of the garage system advance from left to right. H. Events on the right come before events on the left. First the right gate (B1) opens, and shortly before the ladder can enter the garage, the left gate (A1) too. Then the right gate (B2) closes and immediately opens again (B3), allowing the right end of the ladder to pass. In the meantime the left end of the ladder has completely passed the left gate. The fact that this gate closes again immediately afterwards (A2) and opens (A3) no longer has any significance. In this way, the ladder in both inertial systems comes through the garage undamaged. The sequence of events is B1 before A1 before B2 before B3 before A2 before A3.

In connection with the original paradox (with a closed rear wall), two variants should now be discussed:

1a) From the perspective of the garage system, the ladder should come to a standstill in the garage immediately. This is only possible if every part of the ladder is accelerated at the same time from the garage's point of view. Once it has come to rest in this way, it also assumes its rest length again in the garage system, and since this is greater than that of the garage, it will hit both inner walls of the garage at the same time during the expansion process.

Fig. 5

1b) In the ladder system, a problem arises from the fact that the ladder is longer than the garage. How is it possible that the left end of the ladder can hit the inside of the left end of the garage? The solution is that in both systems there will be no simultaneous acceleration of the two ends of the ladder or the two sides of the garage, the transfer of the acceleration from one end of the property to the other end can take place with a maximum of v = c. In the garage system, the right part of the ladder is accelerated first and adopts a speed that gradually approaches that of the garage. The other end of the ladder will only be braked later. This automatically causes these sections of the ladder to contract until the entire ladder is finally grasped. From the perspective of the ladder system, the garage is accelerated, first of all the rear wall. Here, too, the entrance door is only recorded at a later point in time. As a result, it is possible that the left end of the ladder disappears completely into the garage, and the ladder can therefore hit the inner walls of the garage on both sides, but not at the same time.

2a) In contrast to the previous variant, the ladder should not come to a standstill along its entire length at the same time in the garage system, but the standstill is caused by the impact on the rear wall. From the garage's point of view, the right end of the ladder comes to a stop first and consequently expands as it now assumes its rest length. This continues to the other end of the ladder, so that gradually the whole ladder assumes its rest length and consequently also hits the other inside of the garage during the expansion process.

2b) In the ladder system, the problem arises again as to how it should be possible for the left end of the ladder to hit the inside of the left end of the garage. The answer to this question arises from the fact that, according to the theory of relativity, rigid bodies can not exist. Since the acceleration in this case comes from only one point, and the coupling forces in the ladder cannot spread faster than the speed of light, it takes time until the information about the collision reaches the other end of the ladder. As with 1b), the right part of the ladder is first accelerated and takes on a speed that gradually approaches that of the garage. From the point of view of the ladder system, the ladder is compressed like an accordion due to the collision, and the left end of the ladder, which is initially resting, only starts moving when the ladder is already completely enclosed inside the garage. During the expansion process that is now beginning (since the ladder is longer than the garage in the same state of motion), the left end of the ladder will also meet the left inside of the garage.

Panzer paradox

This paradox was first introduced by the physicist Wolfgang Rindler , whereby various varieties of this paradox are also known as the "tank paradox" or "skier paradox".

Let there be a ditch with a "rest length" of 10 m (measured in its rest system or the inertial system in which the ditch is motionless) and a rod moved relative to it with the same rest length. If the relative movement between them is so high that a contraction factor of 10 is reached, then this means that, from the trench perspective, the rod is contracted to 1 m, while the trench remains unshortened. On the other hand, from the point of view of the rod, the trench is contracted to 1 m and the rod is not shortened. This leads to the following seemingly contradicting situation.

Assuming that the trench is closed with a trap door, which is opened when the rod is just above the trench, the rod contracted to 1 m should immediately, i.e. H. simultaneously fall into the 10 m wide trench along its entire length. (In order for this to actually happen, however, there should be an electromagnet in the trench that attracts the rod - because gravity cannot be dealt with within the framework of the special theory of relativity.) For an observer who moves with the rod, however, the trench is contracted to 1 m, and there is no reason for this observer (for the time being) to assume that the 10 m long “rigid” rod will fall into the only 1 m wide trench.

resolution

A rod falls into a ditch at a relativistic speed

The solution to this paradox lies in the fact that the assumption of the observer who is at rest relative to the rod, namely that the rod is “rigid”, is wrong. That is, there are no “ rigid bodies ” in the special theory of relativity, since effects in the body can propagate at the maximum speed of light, while the rigid body of pre-relativistic physics is based on the assumption that effects propagate in it infinitely quickly . In addition, the relativity of simultaneity must be taken into account. The view of the observer resting at the rod, corrected by the special theory of relativity, is thus: The trapdoor does not open at all points at the same time. And since the coupling forces in the rod need time for their effect due to their finite propagation speed (maximum speed of light), the rod cannot maintain its “rigidity” (ie the coupling forces in the rod react too slowly) and will begin immediately at the open points of the trap door to "flow" into the trench due to the action of the magnet. In the event that there is no trap door, the rod would of course begin to flow immediately when the first end of the rod is above the trench.

As soon as the front end of the rod hits the trench wall, gradually, from front to back, parts of the rod are now at rest in the system of rest of the trench, until the entire rod stands still in the forward direction. There is then no longer a system of rest for the rod in which the trench is shorter than the rod, and thus the whole rod can fall into the trench in any case.

On the other hand, it could be argued that, although it has now been proven that the rod falls into the ditch in both inertial systems, it would (if the angle of fall were the same in both systems) hit the opposite wall significantly deeper from the point of view of the rest system of the ditch, since the distance to be covered and thus the flight time are significantly longer here, whereas from the point of view of the staff the trench and thus the distance to be covered is significantly shorter, and thus the point of impact is significantly higher. However, this assessment is wrong: Because the acceleration and thus the angle of fall will be much more pronounced in the rod system (or be subject to relativistic aberration), and thus hit the same point on the opposite wall as in the ditch system despite the shorter distance. This is because it must be taken into account that the electric Coulomb field in the trench is subject to contraction from the point of view of the rod, as is the trench itself. This means that the field lines of the Coulomb field normal to the direction of movement in the rest system of the rod are much closer together are than in the ditch rest system.

In other variants, the scenario of a battle between two armies is also used. One army is now digging a trench which they think is wide enough for the approaching enemy tank to fall into. To be absolutely sure, a strong electromagnet is used for this. The other army, on the other hand, believes that their tank can easily get over the trench they see as contracted. The rest corresponds to the above scheme: the armor will immediately begin to dissolve at the points where it hovers freely over the trench (i.e. with a trap door in the places where the trap door opens first, and without a trap door immediately after reaching the edge).

Another variant involves a skier during a descent . This comes to a crevasse - from the perspective of the glacier system, the contracted skis should fall into it, but from the point of view of the skier, the skis should come over the contracted crevice without any problems. The resolution is the same as above: the skis melt and hit the split wall.

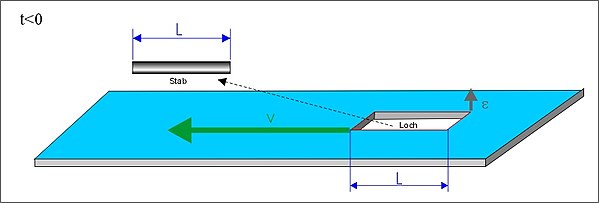
Scale paradox

A rod of length L moves with a speed v parallel to a resting hole also the length L has. At the same time, the rod is still moving towards the hole at a small, vertical speed : ${\displaystyle \epsilon }$

(For the two introductory figures, let us assume that v is so small compared to the speed of light c that no relativistic effects emerge.)

A rod of length L moves with a speed v parallel to a resting hole also the length L has. At the same time, the rod is still moving towards the hole with a small, vertical speed ε

At a suitable point in time t = 0, the rod crosses the resting hole in parallel:

At a suitable point in time t = 0, the rod crosses the resting hole in parallel

• Case (A): The rod moves parallel towards the resting hole.

Viewed from the reference system of the resting hole, the fast moving rod (here with approx. V = 0.94  c ) appears shortened to the length L ' < L due to the length contraction and thus fits comfortably through the hole:

Case (A): When viewed from the reference system of the hole at rest, the rapidly moving rod appears shortened by the length contraction and fits through the hole

• Case (B): The hole moves towards the rod at rest

However, if you look at the situation from the moving system of the rod, the rod is at rest and the hole moves towards the rod at high speed v relative to the rod: (In the figure above at t <0, the hole is still longer L shown, which it has at rest before it is accelerated to v .)

Case (B): viewed from the moving system of the rod, the hole moves relative to the rod with the high speed v

Viewed from the rod, which has the length L in its rest system, the length contraction now affects the moving hole, which only has the length L ' < L , so that the rod no longer fits across the hole:

Case (B): Due to the length contraction of the hole, the rod does not fit through the hole

But that is a contradiction . The dimensions can appear mutually shortened to one another; however, the statement that the rod passes through the hole cannot be made dependent on the choice of the reference system; otherwise the theory of relativity would be contradictory and wrong.

resolution

The description of case (A) (the rod moves parallel towards the resting hole) corresponds to reality and is correctly represented. The description of case (B) (the hole moves towards the rod at rest) was not carried out correctly in the preceding illustration according to the laws of the Lorentz transformation and thus creates the apparent paradox that actually does not exist. When transforming to the system in case (B), it must also be taken into account that not only do the location coordinates change according to the Lorentz transformation and thus lead directly to length contraction, but that the time must also be transformed. This also changes the view of which events appear as simultaneous. In case (A) (hole at rest) the rod crosses the hole in parallel, which means that the front and rear ends of the rod move through the hole simultaneously at time t = 0. The rear end of the rod crosses the hole at location x = 0, the front end of the rod at the location . In case (B), this simultaneity of passage is not retained at the two current hole edge locations, but the time t ' in the rod rest system is calculated according to the Lorentz transformation: ${\displaystyle x_{1}}$

${\displaystyle t^{'}={\frac {t-{\frac {v}{c^{2}}}\cdot x}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

If the rear end of the rod crosses the hole at time t = 0 and at location x = 0, this happens at the following time in the rod rest system:

${\displaystyle t^{'}={\frac {0-{\frac {v}{c^{2}}}\cdot 0}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}=0}$

For the front end of the rod (at time t = 0, at the location in the hole) this happens at the following time in the rod rest system: ${\displaystyle x_{1}}$

${\displaystyle t^{'}={\frac {0-{\frac {v}{c^{2}}}\cdot x_{1}}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}={\frac {-{\frac {v}{c}}\cdot x_{1}}{\sqrt {c^{2}-v^{2}}}}<0}$

The front end of the rod pierced the hole much earlier than the rear end of the rod (viewed in the system that moves with the rod). The fact that the front end of the "resting" rod crosses the approaching hole first clearly means that the hole no longer flies parallel to the rod, but appears tilted, so that the following transformed image for case (B) (The hole moves towards the rod at rest) results in:

If the transformed time is taken into account, the rod and hole no longer move parallel to each other, the two ends of the rod cross the hole at different times, so the rod fits through the hole

In this system, rod and hole no longer fly parallel to each other. It first follows: Simultaneous events in an inertial running in a moved relative thereto inertial not also simultaneously from, and secondly "parallel" lines in other inertial are not parallel: the angle between two spatial directions relatively moving observers differently measured two .

The argument can also be carried out the other way around: If one assumes a rod at rest, towards which a hole actually moves parallel, then the transformation into the system of the hole at rest (case (A)) now generates the tilting of the rod (in the previous one It was exactly the opposite in the illustration, the hole was tilted there and not the rod). The scale paradox can thus be resolved in any case without contradiction within the framework of the theory of relativity.

See also

• Bell's spaceship paradox
• Ehrenfest's paradox

literature

1. ↑ Wolfgang Rindler: Essential relativity . Birkhäuser, Boston 1977, ISBN 3-540-07970-X , pp. 41-42.
2. ↑ ^{a b c d} Eckhard Rebhan: Theoretical Physics I . Spektrum, Heidelberg / Berlin 1999, ISBN 3-8274-0246-8 , pp. 791-793.
3. ↑ ^{a b} Rindler, Wolfgang: Length Contraction Paradox . In: Am. J. Phys. . 29, No. 6, 1961, pp. 365-366. doi : 10.1119 / 1.1937789 .
4. ↑ ^{a b c} Roman Sexl, Herbert K. Schmidt: Space-Time-Relativity . Vieweg, Braunschweig 1979, ISBN 3-528-17236-3 .
5. ↑ Ulrich E. Schröder: Special Theory of Relativity. Verlag Harri Deutsch, 2005, ISBN 3-8171-1724-8 .
6. ^ Richard Lenk: Brockhaus-abc-PHYSIK , Volume 2, 2nd edition, FA Brockhaus Verlag, Leipzig 1989, ISBN 3-325-00192-0 .

Web links

• Physics FAQ: Length paradox
• Physics FAQ: The Barn and the Pole