Geometric frustration

Geometric frustration (also known as frustration for short ) is a phenomenon in condensed matter physics in which the geometric properties of a crystal lattice or the presence of conflicting atomic forces prevent the simultaneous minimization of all interaction energies at a given lattice point. This can lead to highly degenerate ground states with entropy other than 0 even at 0 K (see zero point entropy ). In simpler terms, the substance can never be completely frozen because the structure it forms does not have a single state of minimal energy. Movement at the molecular level still takes place at absolute zero without any energy input.

history

The term frustration in the context of magnetic systems goes back to Gérard Toulouse (1977) and is particularly important for spin glasses .

Magnetic systems with geometric frustration have been studied for many years. Early work included studies of an Ising model on a triangular lattice with antiferromagnetically coupled neighboring spins by GH Wannier published in 1950.

There were later similar attempts at magnets with competing interactions ; H. with different couplings, each of which prefer simple (ferromagnetic or antiferromagnetic) but altogether different structures. In this case, incommensurable spin arrangements can result (e.g. with a spiral structure), as they have been treated since 1959 by Akio Yoshimori , Thomas A. Kaplan , Roger Elliott and others.

A renewed interest in such spin systems arose around two decades later in the context of spin glasses and spatially modulated magnetic superstructures. In spin glasses, the geometric frustration is intensified by stochastic disorder in the interactions. Known spin models with competing or frustrated interactions include the Sherrington-Kirkpatrick model , which describes spin glasses, and the ANNNI model , which represents commensurable and incommensurable magnetic superstructures.

Magnetic order

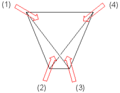
Geometric frustration is an important phenomenon in solid magnetism and has to do with the topological arrangement of spins . A 2D example is shown in Figure 1. Three magnetic ions sit on the corners of a triangular grid with antiferromagnetic interactions between them - since the locations of the (otherwise identical) particles are fixed on the grid, the particles can be distinguished by their location. The energy is minimal when each spin is opposite relative to its neighbors. If the first two spins are anti-parallel, the third is frustrated because its two possible orientations, up and down, result in the same energy. The third spin cannot minimize its interaction energy with both other spins at the same time. Since this occurs for each of the three spins, the ground state is degenerate sixfold ; only the two states in which all spins are up or down have a higher energy.

Similarly, in three-dimensional four spins arranged in a tetrahedron can be geometrically frustrated (Figure 2). If the spins interact antiferromagnetically, they cannot all be aligned antiparallel. There are six closest-neighbor interactions , four of which are antiparallel and therefore energetically “favorable”, but two energetically “unfavorable” interactions remain (here between 1 and 2 and between 3 and 4).

• 

  Figure 1: Antiferromagnetically interacting spins in a triangular arrangement

• 

  Figure 2: Antiferromagnetically interacting spins in a tetrahedral arrangement

Geometric frustration is also possible when the spins are arranged non- collinear . In the case of a tetrahedron with a spin at each corner, which is aligned along the respective axis through the center of the tetrahedron, the spins can be arranged in such a way that they cancel each other out, i.e. there is no net spin (Figure 3). This is equivalent to an antiferromagnetic interaction between each spin pair, and in this case there is no geometric frustration. With such axes, geometric frustration arises when there is ferromagnetic interaction between neighbors such that parallel spins minimize energy. The "best possible" arrangement is shown in Figure 4; there two spins point towards the center and two away from it. The resulting magnetic moment points up and maximizes the ferromagnetic interaction in that direction, but the vector components in other directions cancel each other out; that is, they are arranged antiferromagnetically. There are three different but equivalent arrangements in which two spins point outwards and two inwards, so that the ground state is threefold degenerate.

• 

  Figure 3: Spins along the axes that pass through the center

• 

  Figure 4: Spins with geometric frustration along the axes passing through the center

Mathematical definition

The mathematical definition is analogous to the Wilson loop in quantum chromodynamics : there are energy variables of form

${\displaystyle {\mathcal {H}}=\sum _{G}\,-I_{k_{\nu },k_{\mu }}\,\,S_{k_{\nu }}\cdot S_{k_{\mu }}}$

considered, with

• the graph under consideration ${\displaystyle G}$
• the "exchange energies" between nearest neighbors, which should assume the values ​​± 1 (in given energy units) ${\displaystyle I_{k_{\nu },k_{\mu }}}$
• the inner products of scalar or vectorial spin variables. ${\displaystyle S_{k_{\nu }}\cdot S_{k_{\mu }}}$

If the graph has the (square or triangular) edge areas , the “badge variables”, “loop products” of the shape or appear in the following , which are also referred to as “frustration product”. These frustration products are used to form the sum of all plaques. The result for the individual badge is either +1 or −1. In the negative case, the badge is "geometrically frustrated". ${\displaystyle G}$ ${\displaystyle P}$ ${\displaystyle I_{1,2}I_{2,3}I_{3,4}I_{4,1}}$ ${\displaystyle I_{1,2}I_{2,3}I_{3,1}}$

One can show that the result is gauge invariant  : it does not change if the local values ​​of the exchange integrals and the spins are subjected to the following gauge transformation at the same time:

${\displaystyle I_{i,k}\to \epsilon _{i}I_{i,k}\epsilon _{k},\quad S_{i}\to \epsilon _{i}S_{i},\quad S_{k}\to \epsilon _{k}S_{k}\,.}$

with and as any number ± 1. ${\displaystyle \epsilon _{i}}$ ${\displaystyle \epsilon _{k}}$

But not only the "frustration products", but also other measurable variables, e.g. B. , do not change with such "recalibration" . ${\displaystyle {\mathcal {H}}}$

literature

• David Sherrington, Scott Kirkpatrick: Solvable Model of a Spin-Glass . In: Physical Review Letters . tape 35 , no. 26 , 1975, p. 1792–1796 , doi : 10.1103 / PhysRevLett.35.1792 .
• G. Toulouse: Theory of the frustration effect in spin glasses: I . In: Communications on Physics . tape 2 , no. 4 , 1977, pp. 115-119 .

See also

• Spin ice cream