Hausdorff convergence

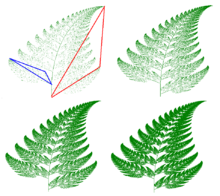
Hausdorff convergence is a mathematical term used to describe that compact subsets of (or a general metric space ) approximate a limit set. It is used in fractal geometry to construct fractals and in differential geometry to prove contradictions. ${\ displaystyle \ mathbb {R} ^ {n}}$

The term Gromov-Hausdorff convergence is more general , which describes the convergence of arbitrary sequences of compact metric spaces (not necessarily subsets of a given space).

definition

The Barnsley fern results from the Hausdorff limit of its finite approximations.

Let be a metric space and a sequence of compact subsets. The sequence converges to the compact set if ${\ displaystyle (X, d)}$ ${\ displaystyle A_ {n} \ subset X}$ ${\ displaystyle A_ {n}}$ ${\ displaystyle A}$

{\ displaystyle \ lim _ {n \ rightarrow \ infty} \ delta (A_ {n}, A) = 0}

applies. This is the Hausdorff distance . ${\ displaystyle \ delta}$

In full meaning of this definition: converges to when it all one there, so for all applies: is the environment of and is in the environment of . ${\ displaystyle A_ {n}}$ ${\ displaystyle A}$ ${\ displaystyle \ epsilon> 0}$ ${\ displaystyle N \ in \ mathbb {N}}$ ${\ displaystyle n> N}$ ${\ displaystyle A}$ ${\ displaystyle \ epsilon}$ ${\ displaystyle A_ {n}}$ ${\ displaystyle A_ {n}}$ ${\ displaystyle \ epsilon}$ ${\ displaystyle A}$

properties

Limits of sequences of convex sets in Euclidean space are convex, limits of sequences of connected sets are connected. In contrast, the limit value of a sequence of path-connected spaces does not always have to be path-connected.

Two convergent sequences and their limits.

The sequence on the right in the picture is a sequence of tori which converges to a circle. The limit value of a sequence of homeomorphic spaces does not necessarily have to be homeomorphic to the individual sequence members, it can even have a lower dimension. ${\ displaystyle A_ {n}}$

The sequence on the right in the picture is a sequence of curves of length which converges to a curve of length . The length of curves, however, so not continuous with respect to Hausdorff convergence, it is lower continuous . Higher-dimensional volumes of surfaces, bodies, etc. are generally neither below nor above semi-continuous with respect to Hausdorff convergence. ${\ displaystyle B_ {n}}$ ${\ displaystyle {\ sqrt {2}}}$ ${\ displaystyle 1}$

Compactness theorem

According to Blaschke's theorem , the following compactness criterion applies to the Hausdorff convergence.

Let be arbitrary, a ball of radius , and a sequence of compact sets, then there is a Hausdorff-convergent subsequence . ${\ displaystyle R> 0}$ ${\ displaystyle B (x_ {0}, R) \ subset \ mathbb {R} ^ {d}}$ ${\ displaystyle R}$ ${\ displaystyle A_ {n} \ subset B (x_ {0}, R)}$

literature

“How Riemannian Manifolds Converge: a Survey” by Christina Sormani, Metric and Differential Geometry: The Jeff Cheeger Anniversary Volume, edited by X. Rong and X. Dai, Progress in Mathematics Vol 297, 27 pp. pdf