Isotomically conjugate points

Isotomically conjugate points and ${\displaystyle P_{1}}$ ${\displaystyle P_{1}}$

Isotomically conjugated points are considered in triangle geometry . They are defined as follows:

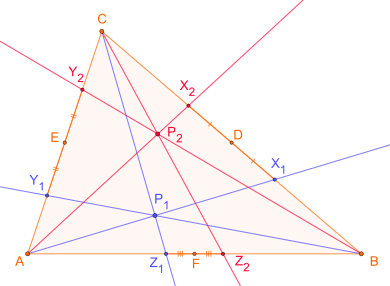
A triangle ABC is given. Let the side centers be denoted by D, E and F. Furthermore, three points X ₁ , Y ₁ and Z _{1 are} given on the pages [BC], [CA] and [AB] , with the straight lines AX ₁ , BY ₁ and CZ ₁ (blue in the sketch) in one point P ₁ cut. If you designate the mirror points of X ₁ , Y ₁ and Z ₁ at the respective side centers (D, E or F) with X ₂ , Y ₂ and Z ₂ , it follows from Ceva's theorem that the straight line AX ₂ , BY ₂ and CZ ₂ (drawn in red) intersect at a point P ₂ . The points P ₁ and P _{2 are} said to be isotomically conjugated to one another.

Examples

• The center of gravity of a triangle is isotomically conjugated to itself.
• The Nagel point and the Gergonne point are isotomically conjugated to one another.

properties

• If a point P _{1 has} the trilinear coordinates , the isotomically conjugate point P _{2 has} the trilinear coordinates . , and stand for the side lengths of the given triangle. ${\displaystyle x:y:z}$ ${\displaystyle {\frac {1}{a^{2}x}}:{\frac {1}{b^{2}y}}:{\frac {1}{c^{2}z}}}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle c}$
• If a point P _{1 has} the barycentric coordinates , the isotomically conjugated point P _{2 has} the barycentric coordinates or equivalent . ${\displaystyle x:y:z}$ ${\displaystyle {\frac {1}{x}}:{\frac {1}{y}}:{\frac {1}{z}}}$ ${\displaystyle yz:zx:xy}$

See also

• Isogonally conjugated points

literature

• Roger A. Johnson : Advanced Euclidean Geometry . Dover 2007, ISBN 978-0-486-46237-0 , pp. 157-159, 278 (first published in 1929 by the Houghton Mifflin Company (Boston) under the title Modern Geometry )

Web links

Commons : Isotomic Conjugates  - Collection of images, videos and audio files

• Eric W. Weisstein : Isotomic Conjugate . In: MathWorld (English).
• Paul Yiu: Isotomic and isogonal conjugates - Chapter 12 of a geometry script (PDF, 10 pages)
• Navneel Singhal: Isotomic and isogonal conjugates (PDF, 12 pages)