Jacobi field

A Jacobi field or, more precisely Jacobi vector field (named after Carl Gustav Jacob Jacobi ) is a vector field along a geodesic , the solution of the Jacobi equation is. Considered clearly, it represents the displacement vector field between infinitesimally neighboring geodesics on a Riemannian or pseudoriemannian manifold . This concept is used in differential geometry and in general relativity . The study of Jacobi fields is central to the proof of Cartan-Hadamard's theorem .

Jacobi equation

The Jacobi equation is a differential equation for a vector field along a geodesic and relates the curvature of the manifold to the second derivative of the Jacobi field sought.

Let it be a geodesic with a tangential vector field . A smooth vector field along is called a Jacobi field if it is the Jacobi equation ${\displaystyle c\colon (a,b)\rightarrow M}$ ${\displaystyle c'}$ ${\displaystyle Y\colon (a,b)\rightarrow TM}$ ${\displaystyle c}$

${\displaystyle \nabla _{c'}^{2}Y+R(Y,c')c'=0}$

Fulfills. The term denotes the curvature tensor and the longitudinal covariant derivative induced by the Levi-Civita relationship . ${\displaystyle R(\cdot ,\cdot )\cdot }$ ${\displaystyle \nabla _{c'}}$ ${\displaystyle \nabla }$ ${\displaystyle c}$

The Jacobi equation is a linear ordinary differential equation of the second order.

In general, a Jacobi field can have components tangential and orthogonal to the geodesic. Tangential Jacobele fields have the simple shape

${\displaystyle Y(t)=ac'(t)+btc'(t)}$

for real parameters and . Any Jacobi fields have the shape ${\displaystyle a}$ ${\displaystyle b}$

${\displaystyle Y(t)=Y_{\perp }(t)+ac'(t)+btc'(t)}$,

where a Jacobi field is orthogonal to . For the investigation of conjugate points and the Morse index theory, one therefore usually restricts oneself to the consideration of orthogonal Jacobi fields. ${\displaystyle Y_{\perp }}$ ${\displaystyle c}$

By choosing coordinates, the Jacobi field can be written as , where the parallel orthonormal vector fields are longitudinal , and thus the Jacobi equation is obtained in coordinates: ${\displaystyle Y(t)=\sum \limits _{i=1}^{m}y_{i}(s)X_{i}(s)}$ ${\displaystyle X_{i}}$ ${\displaystyle c}$

${\displaystyle y_{i}''(t)+\sum \limits _{j=1}^{m}y_{j}(t)g(R(c',X_{j})c',X_{i})(t)=0}$

In this form it is easy to see that a unique solution exists for given initial conditions . ${\displaystyle Y(0)=u,Y'(0)=v}$

Example: Jacobi field on the 2-sphere

Representation of a sphere.
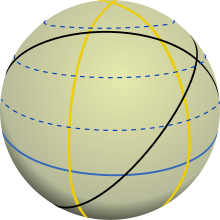
All of the solid lines in this picture are great circles . The dashed lines are the parallels . The yellow lines are the longitudes

The spherical surface can serve as an illustrative example. In the canonical metric on the sphere, which one gains by embedding in , the geodesics are the great circles . All great circles that run through a point intersect again at the antipodal point of this point. These great circles together with the two points describe the longitudes and the poles of a spherical coordinate system. The Jacobi field along these longitude circles is tangential to the sphere at every point and perpendicular to the longitude circles. The integral curves of the Jacobi field are therefore the circles of latitude. The lines of the circles of latitude in the adjacent picture can be understood as vectors of the Jacobi field at this point. Here it becomes clear that the Jacobi field describes the distance between neighboring geodesics and disappears in the poles. The two poles are therefore conjugate points. ${\displaystyle \mathbb {R} ^{3}}$

motivation

The definition of the Jacobi equation is based on the investigation of the energy functional in the context of Riemannian geometry . This functional is defined as follows for all smooth curves on the Riemannian manifold : ${\displaystyle c:[a,b]\to M}$ ${\displaystyle (M,g)}$

${\displaystyle E(c)={\frac {1}{2}}\int \limits _{a}^{b}g(c'(t),c'(t))dt}$

The name energy functional can easily be understood in the context of classical mechanics, in which the kinetic energy of a particle is defined by. As known from Hamilton's principle , a physical particle will choose a path that minimizes energy. So if we are interested in which orbits these are in the context of Riemannian geometry , we have to calculate the variation of this functional. For this we define the variation of a curve as , whereby we abbreviate the respective curve with , whereby our original curve is. With the help of the theory of the fiber bundle and the relationship (differential geometry) we can now calculate the first variation: ${\displaystyle E_{\mathrm {kin} }={\frac {1}{2}}v^{2}}$ ${\displaystyle h:[a,b]\times (-\epsilon ,\epsilon )\to M}$ ${\displaystyle h(t,s)=c_{s}(t)}$ ${\displaystyle c_{0}(t)=c(t)}$

${\displaystyle {\frac {d}{dt}}{\bigg \vert }_{s=0}E(c_{s})=g(Y(t),c'(t)){\bigg \vert }_{a}^{b}-\int \limits _{a}^{b}g(Y(t),\nabla _{c'(t)}c'(t))\mathrm {d} t}$

Interestingly, for zeros of this variation in the case of a variation with fixed endpoints (i.e. ) we find exactly the definition of a geodesic . So we find that geodesics in Riemannian geometry describe the curves that satisfy the Hamiltonian principle in the case of . To understand the definition of the Jacobele fields we have to go one step further. So we choose an extreme point of the first variation, that is, a geodesic. The second variation then results as ${\displaystyle c_{s}(a)=p}$ ${\displaystyle c_{s}(b)=q}$ ${\displaystyle \forall s\in (-\epsilon ,\epsilon )}$ ${\displaystyle \nabla _{c'(t)}c'(t)=0}$ ${\displaystyle {\mathcal {L}}=E_{\mathrm {kin} }}$ ${\displaystyle c(t)}$

${\displaystyle {\frac {d^{2}}{dt^{2}}}{\bigg \vert }_{s=0}E(c_{s})=\left[g(\nabla _{\partial _{s}}^{h}Y(t),c'(t))+g(\nabla _{\partial _{t}}^{h}Y(t),Y(t))\right]_{a}^{b}+\int \limits _{a}^{b}g(Y(t),\nabla _{\partial _{t}}^{2}Y(t)+R(c',Y)c'(t))\mathrm {d} t}$

So we see that the second variation of the energy functional opens the definition of Jacobi fields.

Lorentz index form and conjugate points

Like the Riemannian index theory, Lorentz's index theory considers geodesics on a special case of pseudoriemannian manifolds and examines these geodesics for the occurrence of conjugate points. Two points , along a geodesic is called conjugated to each other when a non-trivial smooth Jacobi field along exists that in and disappears. ${\displaystyle p=c(a)}$ ${\displaystyle q=c(b)}$ ${\displaystyle c}$ ${\displaystyle c}$ ${\displaystyle p}$ ${\displaystyle q}$

Let be the space of the section-wise smooth orthogonal vector fields along a geodesic , that is, for be and for all . The bilinear symmetrical index form ${\displaystyle V^{\perp }(c)}$ ${\displaystyle c\colon [a,b]\rightarrow M}$ ${\displaystyle Y\in V^{\perp }(c)}$ ${\displaystyle Y(t)\in T_{c(t)}M}$ ${\displaystyle \langle Y(t),c'(t)\rangle =0}$ ${\displaystyle a\leq t\leq b}$

${\displaystyle I\colon \;V^{\perp }(c)\times V^{\perp }(c)\rightarrow \mathbb {R} }$

is defined by

${\displaystyle I(X,Y)=-\int _{a}^{b}\langle X',Y'\rangle -\langle R(X,c')c',Y\rangle \,\mathrm {d} t}$ For ${\displaystyle X,Y\in V^{\perp }(c).}$

In the Riemannian index theory, the sign of the index form is chosen to be positive. If is smooth, a partial integration can be performed and the following applies: ${\displaystyle X}$

${\displaystyle I(X,Y)=-\langle X',Y\rangle |_{a}^{b}+\int _{a}^{b}\langle X''+R(X,c')c',Y\rangle \,\mathrm {d} t}$

For with , that is, this simplifies further to: ${\displaystyle Y\in V^{\perp }(c)}$ ${\displaystyle Y(a)=Y(b)=0}$ ${\displaystyle Y\in V_{0}^{\perp }(c)}$

${\displaystyle I(X,Y)=\int _{a}^{b}\langle X''+R(X,c')c',Y\rangle \,\mathrm {d} t}$

The index form is closely related to conjugate points: For is equivalent to whether a Jacobi field is or whether applies to all . So the end points are conjugated along the geodesics if and only if the bilinear form is degenerate. ${\displaystyle Y\in V_{0}^{\perp }(c)}$ ${\displaystyle Y}$ ${\displaystyle I(Y,Z)=0}$ ${\displaystyle Z\in V_{0}^{\perp }(c)}$ ${\displaystyle c}$ ${\displaystyle I}$

Variation of geodesics

A variation of a geodesic is a smooth map ${\displaystyle c:[a,b]\rightarrow M}$

${\displaystyle \alpha :[a,b]\times (-\varepsilon ,\varepsilon )\rightarrow M}$

for one with . Usually one demands fixed endpoints: and for everyone . The canonical variation with fixed end points is precisely the exponential mapping of vector fields scaled with s ${\displaystyle \varepsilon >0}$ ${\displaystyle \alpha (t,0)=c(t)}$ ${\displaystyle \alpha (a,s)=c(a)}$ ${\displaystyle \alpha (b,s)=c(b)}$ ${\displaystyle s\in (-\varepsilon ,\varepsilon )}$

${\displaystyle Y\in V_{0}^{\perp }(c)}$: . ${\displaystyle \alpha (t,s)=\operatorname {exp} _{c(t)}(sY(t))}$

The variation vector field V of the variation is the vector field V (t) along c (t) with . For the canonical variation the variation vector field is therefore Y (t). ${\displaystyle \alpha }$ ${\displaystyle V(t)=d/ds(\alpha (t,s))|_{s=0}}$

The 2nd variation of the Lorentzian length

${\displaystyle L''(0)=(d^{2}/ds^{2}L(s))|_{s=0}\,}$(with ), ${\displaystyle L(s)=L(t\rightarrow \alpha (t,s))}$

geodetic variation is now given by the above-described index form: . It follows that the variation at I (Y, Y)> 0 results in neighboring time-like curves that also connect c (a) with c (b), but with a greater length ${\displaystyle L''(0)=I(Y,Y)}$ ${\displaystyle \alpha }$

${\displaystyle L(\alpha )>L(c)\,}$

exhibit. So that the time-like geodesic is maximal, i.e. its length corresponds to the Lorentzian distance between its endpoints, I must be negative semidefinite on c.

literature

• Beem, JK, Ehrlich, PE, Easley, KL: Global Lorentzian Geometry, Pure and Applied Mathematics 202, 2nd Edition. New York: Marcel Dekker, Inc. 1996