Potato paradox

The potato paradox describes a surprising result in the careless handling of percentages when determining the ratio of dry matter and water in potatoes. The problem of understanding can be transferred to similar facts. It is not a mathematical paradox in the sense of an antinomy (example: Russell's paradox ), but a playful puzzle with a punch line . It draws attention to the importance of understanding the task in detail by analyzing the problem before starting to calculate.

The linguistically deliberately misleading and counterfactual task is usually:

“100 kilograms of potatoes were harvested with 99 percent water. In the sun they dried up 'a little'. 'The potatoes' now only consist of 98 percent water, but are otherwise intact . How much do the potatoes weigh now? "

In variants of the task there are also time specifications such as “overnight”.

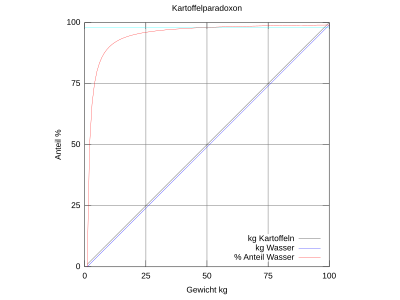
Plot of the percentage of water in the total amount as a red line.
The gray line describes the total weight of the potatoes and starts at the top right with 100 kg. As the potatoes dry out, the weight drops to the left on the diagonal line.
The blue line of the water mass lies immediately below the gray diagonal, since the potatoes in the task consist almost entirely of water.
The light blue 98% line is shown at the very top.

The surprising punch line of the riddle: After drying, the potatoes only weigh 50 kilograms (49 kilograms of water and 1 kilogram of dry matter).

In the online encyclopedia MathWorld , this arithmetic task is called potato paradox . It is misleading that the same term is also used for the Giffen paradox , which is said to have applied during the Great Famine in Ireland to the increasing purchase of potatoes despite rising prices. It describes a surprising, but psychologically and economically easily explainable consumer behavior and has nothing in common with the problem of the potato paradox other than the name.

Explanation of the bill

With two different dimensions

The proportion of dry matter in the 1st total mass before drying ( ) is one percent and as a proportion of the 2nd total mass after drying ( ) two percent, i.e. it has doubled. However, the actual dry matter is set to the same weight value (which is why we can mathematically equate both representations of the dry matter), so the total weight has been halved mathematically. ${\ displaystyle {\ text {M}} _ {1}}$ ${\ displaystyle {\ text {M}} _ {2}}$

{\ displaystyle {\ begin {aligned} 1 \, \% \ cdot {\ text {M}} _ {1} & = 2 \, \% \ cdot {\ text {M}} _ {2} \\ { \ text {M}} _ {2} & = {\ frac {1} {2}} {\ text {M}} _ {1} \ end {aligned}}}

In this sense , the potato paradox is a three- rule problem that is so ambiguously worded that, intuitively and with a rough calculation, one would expect a completely different result.

The control calculation confirms: 2% dry matter of 50 kg is still 1 kg and 98% water of 50 kg total weight corresponds to the 49 kg that are required to achieve 50 kg of potatoes.

With parts instead of percentages

If one part of water evaporates from 100 parts (99 parts water, 1 part dry matter), 99 parts (98 parts water, 1 part dry matter) remain. So there is a part missing. If these 99 parts are extrapolated to 100 percent, this results in around 98.99% water and 1.01% dry matter.

Only when 50 parts of water have evaporated, 50 parts (49 parts of water, 1 part of dry matter) remain, this corresponds to the ratio of 98% water and 2% dry matter.

The following table shows how much water evaporates if the proportion of water mass in relation to the constant dry mass is only reduced by one percentage point.

The ratio is *slowly* changing
Parts of water mass	Parts of dry matter	Share totally	% Water content
${\ displaystyle 99}$	${\ displaystyle 1}$	${\ displaystyle 100}$	${\ displaystyle 99 \%}$
${\ displaystyle 98}$	${\ displaystyle 1}$	${\ displaystyle 99}$	${\ displaystyle 98 {,} {\ overline {98}} \%}$
${\ displaystyle 90}$	${\ displaystyle 1}$	${\ displaystyle 91}$	${\ displaystyle 98 {,} 9010989 \%}$
${\ displaystyle 50}$	${\ displaystyle 1}$	${\ displaystyle 51}$	${\ displaystyle 98 {,} 03921569 \%}$
${\ displaystyle 49}$	${\ displaystyle 1}$	${\ displaystyle 50}$	${\ displaystyle 98 \%}$

Typical fallacy

The result seems counter-intuitive, as one might think that the water content of the original starting material would only decrease by one percentage point (99% −1%). This misjudgment is reinforced by the misleading and factually incorrect information in the task, the potatoes "dried out" in the sun.

If you do not consider that due to the water content of 98% of the new 2nd total mass, the dry mass now accounts for 2%, the potatoes seem to still weigh 99 kilograms after drying, since on a cursory glance only one percent of the water content has evaporated and one percent the original mass corresponded to one kilogram.

This result would be mathematically correct if the task had been: The water content after drying is 98% of the original total mass.

The fallacy is based primarily on the assumption that the water content of the starting material has decreased by one percentage point, while it was actually stated that it has decreased by one percentage point compared to the dry matter . As a result, the proportion of dry matter must have doubled from one percent to two percent .

With a different formulation of the task, the correct result would be much easier to guess: "The potatoes dry out so much that the ratio of dry matter to total weight doubles."

Actual weight ratios

In fact, raw potatoes with their pulp and skin contain around 80 percent water and after six months of storage lose between 6 and 15 percent of their original weight, i.e. 7.2-18 percent of their original water content through evaporation. The weight loss during storage is sensibly expressed as a percentage of the original total weight.

The puzzle is also formulated with watermelons , which have 91.45 percent water. Winter melons even have 96.10 percent, unpeeled cucumbers 95.23 and peeled 96.73 percent.

Web links

Eric W. Weisstein : Potato Paradox . In: MathWorld (English).

Individual evidence

↑ Derrick Niederman: The Puzzler's Dilemma: From the Lighthouse of Alexandria to Monty Hall, a Fresh Look at Classic Conundrums of Logic, Mathematics, and Life . Penguin, 2012, ISBN 978-1-101-56087-7 ( google.de [accessed March 30, 2017]).

↑ John de Pillis: 777 Mathematical Conversation Starters . MAA, Washington DC 2002, ISBN 978-0-88385-540-9 ( google.de [accessed on March 30, 2017] In this description, the potatoes dry out "overnight").

↑ Gerald P. Dwyer, Cotton M. Lindsay: Robert Giffen and the Irish potato . In: The American Economic Review . tape 74 , no. March 1 , 1984.

↑ According to the USDA National Nutrient Database .

↑ How high are the inevitable storage losses after a six-month storage period? In: toffi.net. Retrieved May 18, 2019.

↑ Albrecht Beutelspacher, Marcus Wagner: Why cows like to graze in a semicircle . 1st edition. Herder Verlag, Freiburg im Breisgau / Basel / Vienna 2012, ISBN 978-3-451-06295-7 , p. 48 .

[1] Derrick Niederman: The Puzzler's Dilemma: From the Lighthouse of Alexandria to Monty Hall, a Fresh Look at Classic Conundrums of Logic, Mathematics, and Life . Penguin, 2012, ISBN 978-1-101-56087-7 ( google.de [accessed March 30, 2017]).

[2] John de Pillis: 777 Mathematical Conversation Starters . MAA, Washington DC 2002, ISBN 978-0-88385-540-9 ( google.de [accessed on March 30, 2017] In this description, the potatoes dry out "overnight").