Lamination (math)

In mathematics , laminations generalize the topological notion of foliation .

Laminations are important in complex dynamics, especially in the theory of iteration of quadratic maps .

Laminations of a topological space

It is a Hausdorff room . A lamination is given by an open cover and homeomorphisms ${\ displaystyle X}$ ${\ displaystyle \ textstyle X = \ bigcup _ {i} U_ {i}}$

{\ displaystyle \ phi \ colon U_ {i} \ to D_ {i} \ times T_ {i}}

,

where an open subset is one and any topological space. ${\ displaystyle D_ {i}}$ ${\ displaystyle \ mathbb {R} ^ {n}}$ ${\ displaystyle T_ {i}}$

A lamination of the circular disk. The edges of the leaves form a lamination of the circle.

Laminations of manifolds

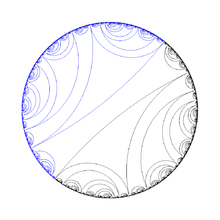
Let it be a manifold. A -dimensional lamination of is a decomposition of a closed subset of into connected submanifolds of the same dimension (the leaves of the lamination), so that there is an overlap of by maps homeomorphic , in which the intersections of the leaves with the maps the hyperplanes for each one correspond. ${\ displaystyle M}$ ${\ displaystyle k}$ ${\ displaystyle M}$ ${\ displaystyle M}$ ${\ displaystyle k}$ ${\ displaystyle M}$ ${\ displaystyle I ^ {k} \ times I ^ {nk}}$ ${\ displaystyle I ^ {k} \ times \ left \ {y \ right \}}$ ${\ displaystyle y \ in I ^ {nk}}$

Laminations of the circle

A slightly different terminology is used in the theory of dynamic systems when it comes to lamination of the circle. In this case, the leaves should not be contiguous, but rather pairs of points, with different pairs of points not being allowed to be intertwined . (Ie if there is a leaf and another leaf, then and both must be in the same connected component of.) ${\ displaystyle \ left \ {x_ {1}, x_ {2} \ right \}}$ ${\ displaystyle \ left \ {y_ {1}, y_ {2} \ right \}}$ ${\ displaystyle y_ {1}}$ ${\ displaystyle y_ {2}}$ ${\ displaystyle S ^ {1} \ setminus \ left \ {x_ {1}, x_ {2} \ right \}}$

If you think of the circle as the edge at infinity of the hyperbolic plane , the lamination of the circle corresponds exactly to the geodetic lamination of the hyperbolic plane. (The edges of two geodesics are not entwined if and only if the two geodesics are disjoint.)

Applications

Special classes of laminations are important in low-dimensional topology and dynamics.

In the theory of 3-manifolds , one is particularly interested in essential laminations .
In the theory of (hyperbolic) surfaces , geodetic lamination is important.
In the theory of low-dimensional dynamic systems, lamination of the circle is used, for example to study the angle-doubling mapping .
In the complex dynamics are used to Sullivan laminations by Riemann surfaces (engl .: Riemann surface laminations ), these are laminations by complex submanifolds locally equivalent to a product circular disk × Cantor set .

literature

Danny Calegari : Foliations and the geometry of 3-manifolds. Oxford Mathematical Monographs. Oxford University Press, Oxford, 2007. ISBN 978-0-19-857008-0

Web links

Lamination (Encyclopedia Mathematica)
D. Sullivan: Quadratic differentials and renormalization conjectures (Appendix)
A. Candel: Uniformization of Surface Laminations