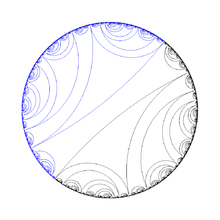
Geodesic lamination

In mathematics , geodetic lamination is an important tool in low-dimensional topology, especially when studying dynamics on surfaces .

definition

Geodetic lamination of a closed hyperbolic surface with two closed geodesics and a third non-closed geodesics spiraling into both.

Geodetic lamination of the hyperbolic plane.

A geodesic lamination is a lamination of a hyperbolic surface , the leaves of which are geodesic .

The set of all geodetic laminations of a hyperbolic surface is denoted by. ${\displaystyle S}$ ${\displaystyle {\mathcal {L}}(S)}$

More generally, geodetic laminations of arbitrary Riemannian manifolds can be defined as laminations whose leaves are totally geodetic submanifolds . In the higher-dimensional topology and dynamics, however, geodesic lamination play a smaller role and there are fewer examples of geodesic lamination in higher dimensions, which is why lamination of hyperbolic surfaces is usually meant when geodesic lamination is mentioned without further addition.

Examples

• A union of closed simple geodesics is a geodesic lamination.
• A geodesic spiraling into a closed curve forms a geodesic lamination together with this closed curve.
• The stable and unstable lamination of a pseudo-Anosov diffeomorphism is geodetic lamination.

Transverse dimensions

Be a geodetic lamination of a surface . A transversal measure assigns a measure to each transversal line , compatible with restrictions and invariant under the homotopias of transversal arcs that are mapped onto them . ${\displaystyle L}$ ${\displaystyle S}$ ${\displaystyle L}$ ${\displaystyle L}$

The carrier of a transversal measure is the union (over all transversal lines ) of the carriers of the induced measures . ${\displaystyle \operatorname {supp} (\mu )\subset L}$ ${\displaystyle \mu }$ ${\displaystyle k}$ ${\displaystyle \mu {\big |}_{k}}$

A measured geodesic lamination (engl .: Measured geodesic lamination ) consists of a geodesic lamination and a transverse dimension with . ${\displaystyle L}$ ${\displaystyle \mu }$ ${\displaystyle \operatorname {supp} (\mu )=L}$

The set of all measured geodetic lamination of a hyperbolic surface is denoted by. ${\displaystyle S}$ ${\displaystyle {\mathcal {ML}}(S)}$

Topologies on L (S) and ML (S)

The set of all geodetic laminations has a natural topology defined by the Hausdorff metric on the set of all closed subsets of . With this topology is a compact space . ${\displaystyle S}$ ${\displaystyle {\mathcal {L}}(S)}$

The topology on the set of all measured geodetic laminations is defined as the weak topology with respect to the family of semi-norms ${\displaystyle {\mathcal {ML}}(S)}$

${\displaystyle (L,\mu )\mapsto \left|\int _{k}\phi \,d\mu \right|,(L,\mu )\in {\mathcal {ML}}(S)}$,

where all continuous functions are traversed on lines that are too transversal . That is, a sequence converges to if and only if ${\displaystyle \phi }$ ${\displaystyle \phi \colon k\to \mathbb {R} }$ ${\displaystyle L}$ ${\displaystyle k}$ ${\displaystyle (L_{n},\mu _{n})}$ ${\displaystyle (L,\mu )}$

• ${\displaystyle L_{n}\to L}$in the Hausdorff topology (in particular, routes that are too transverse are also transversal to for sufficiently large ) ${\displaystyle L}$ ${\displaystyle L_{n}}$ ${\displaystyle n}$
• ${\displaystyle \left|\int _{k}\phi \,d\mu _{n}-\int _{k}\phi \,d\mu \right|\to 0}$for all continuous functions on lines that are too transversal . ${\displaystyle \phi \colon k\to \mathbb {R} }$ ${\displaystyle L}$ ${\displaystyle k}$

Minimality, maximality, completeness

A geodesic lamination is called minimal if every half-sheet lies close to the union of all sheets . Every minimal geodetic lamination is (in the topology above) the limit of a series of simple closed curves .

A geodesic lamination is called maximal if the complement of the union of the leaves is a union of ideal triangles and (in the case of dotted areas ) simply dotted monogons. It is called complete if it is the maximum and limit value of a series of simple closed curves. Any minimal geodesic lamination is included in a full geodesic lamination.

Every geodesic lamination is a finite union of disjoint minimal geodesic laminations and individual leaves that are either simple closed curves or spiral around them.

literature

• Francis Bonahon : Geodesic laminations on surfaces. Laminations and foliations in dynamics, geometry and topology (Stony Brook, NY, 1998), 1-37, Contemp. Math., 269, Amer. Math. Soc., Providence, RI, 2001.

Web links

• Francis Bonahon: Closed curves on surfaces (pdf)

Individual evidence

1. ↑ Bonahon, "Geodesic laminations on surfaces", op.cit., Prop. 1
2. ↑ A more detailed explanation of this definition can be found in Chapter 2.1 of Bonahon, "Closed curves on surfaces", op.cit.
3. ↑ Canary-Epstein-Green: Notes on notes of Thurston. Analytical and geometric aspects of hyperbolic space (Coventry / Durham, 1984), 3-92, London Math. Soc. Lecture Note Ser., 111, Cambridge Univ. Press, Cambridge, 1987.
4. ↑ Hamenstädt: Geometry of the mapping class groups. I. Boundary amenability. Invent. Math. 175 (2009), no. 3, 545-609.
5. ↑ Canary-Epstein-Green, op.cit.