Max-flow-min-cut theorem

In the field of graph theory , the Max-Flow-Min-Cut-Theorem describes a sentence that gives a statement about the relationship between maximum flows and minimum cuts in a flow network . The sentence says:

A maximum flow in the network has exactly the value of a minimum cut.

The theorem is a generalization of Menger's theorem . He was independently proven in 1956 by LR Ford Jr. and DR Fulkerson , as well as P. Elias , A. Feinstein and CE Shannon .

Definitions

Let be a finite directed graph with the nodes and the edges . Every edge from node to node has a non-negative capacity. There is also a source node where the network flow begins and a destination node where the network flow ends. ${\displaystyle G(V,E)}$ ${\displaystyle V}$ ${\displaystyle E}$ ${\displaystyle (u,v)}$ ${\displaystyle u}$ ${\displaystyle v}$ ${\displaystyle c(u,v).}$ ${\displaystyle s}$ ${\displaystyle t}$

A section is a division of the nodes perpendicular to the network flow into two disjoint subsets and for which applies, and . The capacity of a cut is the sum of all edge capacities from to , i.e. ${\displaystyle S}$ ${\displaystyle T}$ ${\displaystyle s\in S}$ ${\displaystyle t\in T}$ ${\displaystyle (S,T)}$ ${\displaystyle S}$ ${\displaystyle T}$

${\displaystyle c(S,T)=\sum _{u\in S,v\in T|(u,v)\in E}c(u,v)}$.

sentence

The following three statements are equivalent:

1. ${\displaystyle f}$is the maximum flow in . ${\displaystyle G}$
2. The residual network does not contain an augmenting path . ${\displaystyle G_{f}}$
3. For at least one cut , the value of the flow is equal to the capacity of the cut : ${\displaystyle (S,T)}$ ${\displaystyle |f|=c(S,T)}$

Evidence sketch

• ${\displaystyle 1\Rightarrow 2}$If there were an augmenting path, one could enlarge the river along it; thus the flow cannot have been maximal.
• ${\displaystyle 2\Rightarrow 3}$If there is no augmenting path, then divide the graph into , the nodes reachable in the residual network, and , the rest. Then is (if it weren't for 0, it would have been reachable). Then for this cut . ${\displaystyle S}$ ${\displaystyle s}$ ${\displaystyle T}$ ${\displaystyle c(S,T)-|f|=0}$ ${\displaystyle T}$ ${\displaystyle |f|=c(S,T)}$
• ${\displaystyle 3\Rightarrow 1}$If it were n't for the maximum, it could be enlarged. Since the capacity of each cut is less than or equal to, the capacity cannot yet be used for at least one cut; in addition, no section applies , because otherwise there would be no augmenting path for the flow enlargement and the flow would be maximal. ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle |f|=c(S,T)}$

In particular, this shows that the maximum flow is equal to the minimum cut: because of 3. it has the size of at least one cut, i.e. at least the smallest, and because of 2. also at most this value, because the residual network already reaches the size of the smallest cut can no longer contain an augmenting path. ${\displaystyle |f|}$

example

A network with maximum flow and three minimum cuts

The residual network of the example network

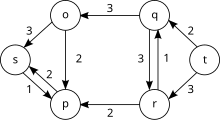
Let the flow network with the nodes be given, and a maximum flow from the source to the sink of size 5. ${\displaystyle V=\{s,o,p,q,r,t\}}$ ${\displaystyle s}$ ${\displaystyle t}$

There are three minimal cuts in this network:

cut	capacity
${\displaystyle S_{1}=\{s,p\},T=\{o,q,r,t\}}$	${\displaystyle c(s,o)+c(p,r)=3+2=5}$
${\displaystyle S_{2}=\{s,o,p\},T=\{q,r,t\}}$	${\displaystyle c(o,q)+c(p,r)=3+2=5}$
${\displaystyle S_{4}=\{s,o,p,q,r\},T=\{t\}}$	${\displaystyle c(q,t)+c(r,t)=2+3=5}$

Note: For all other cuts, the sum of the capacities (not to be confused with the flow) of the outgoing edges is greater than or equal to 6. For example, there is no minimum cut because the sum of the capacities of the outgoing edges is the same . Furthermore, there is no minimum cut, although and are fully used; because there is still an edge (r, q) of the remaining capacity in the residual network . ${\displaystyle S=\{s,o\},T=\{q,p,r,t\}}$ ${\displaystyle c(o,q)+c(o,p)+c(s,p)=3+2+3=8}$ ${\displaystyle S_{5}=\{s,o,p,r\},T=\{q,t\}}$ ${\displaystyle (o,q)}$ ${\displaystyle (r,t)}$ ${\displaystyle G_{f}}$ ${\displaystyle c_{f}(r,q)=c(r,q)-f(r,q)=0-(-1)=1}$

Algorithm for finding minimal cuts

There are different algorithms for finding minimal cuts. The following algorithm finds the edges of a minimal cut directly from the residual network and thus makes use of the properties of the Max-Flow-Min-Cut theorem. For example, the residual flow graph can be generated using the Ford and Fulkerson algorithm.

 ${\displaystyle G=(V,E)}$ ein endlicher gerichteter Graph mit einer Quelle  ${\displaystyle s}$, einer Senke  ${\displaystyle t}$ und jede Kante habe eine nichtnegative Kapazität.
findeKantenEinesMinCut( ${\displaystyle G}$)
1  ${\displaystyle G_{f}\leftarrow }$Residualnetzwerk( ${\displaystyle G}$)
2  ${\displaystyle S\leftarrow \emptyset }$
3  ${\displaystyle T\leftarrow \emptyset }$
4 Für jeden Knoten  ${\displaystyle v\in V}$
5  Wenn Pfad( ${\displaystyle s,v}$) in  ${\displaystyle G_{f}}$ existiert
6  dann  ${\displaystyle S\leftarrow S\cup \{v\}}$
7  ansonsten  ${\displaystyle T\leftarrow T\cup \{v\}}$
8  ${\displaystyle C\leftarrow \emptyset }$
9 Für jede Kante  ${\displaystyle e\in E}$
10 Wenn startKnoten( ${\displaystyle e}$) ${\displaystyle \in S}$ und endKnoten( ${\displaystyle e}$) ${\displaystyle \in T}$ liegt
11  dann  ${\displaystyle C\leftarrow C\cup \{e\}}$
12  ${\displaystyle C}$ ist jetzt die Menge der Kanten für einen minimalen Schnitt

${\displaystyle C}$would contain the cut edges of in the example above . ${\displaystyle S_{1}}$

literature

• Thomas H. Cormen, Charles E. Leiserson , Ronald L. Rivest , Clifford Stein: Introduction to Algorithms . Second edition. MIT Press and McGraw-Hill, 2001, ISBN 0-262-03293-7 . Chapter 26: Maximum Flow , pp. 643-700.
• Santanu Saha Ray: Graph Theory with Algorithms and its Applications . Springer India, New Delhi a. a. 2013, ISBN 978-81-322-0749-8 , pp. 162-165 .

Web links

• Max-Flow Min-Cut Animation (English)
• Max-Flow Problem: Ford-Fulkerson Algorithm (English)

Individual evidence

1. ^ LR Ford Jr., DR Fulkerson: Maximum flow through a network . In: Canad. J. Math. . 8, 1956, pp. 399-404. doi : 10.4153 / CJM-1956-045-5 .
2. ^ P. Elias, A. Feinstein, CE Shannon: Note on Maximum Flow Through a Network . In: IRE Trans. On Information Theory, IT . 2, No. 4, 1956, pp. 117-119. doi : 10.1109 / TIT.1956.1056816 .