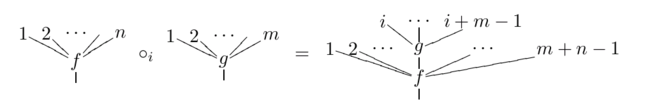Operade

An operade is an algebraic structure that is particularly important in topology , but also in many other applications and leaves room for deformations ( homotopy in the topology) of the underlying objects. Operads generally consist of a set of operations (or functions) with several inputs and one output and the algebra of executing these operations one after the other is considered. The nesting of the successive execution of operations is often represented geometrically in the form of trees .

They were first introduced in algebraic topology in the early 1970s by J. Michael Boardman and Rainer Vogt and by J. Peter May in order to understand the homotopy of higher loop spaces. May also coined the term from operation and monad. The theory of operads experienced a boom in the 1990s, when Maxim Kontsevich , Mikhail Kapranov and Victor Ginzburg showed that some dualities in rational homotopy theory could be explained as Koszul dualities of operads. In homotopy theory, they serve to describe the hierarchies of higher homotopias and have also been used, for example, in mathematical physics and graph theory.

definition

A non-symmetric operad consists of the sequence of the sets of operations on n variables including the identity operation. The following connection of a function on n variables with an operation on m variables is considered: ${\displaystyle P(n)}$ ${\displaystyle f\circ _{i}g}$ ${\displaystyle f\in P(n)}$ ${\displaystyle g\in P(m)}$

${\displaystyle f\circ _{i}g=f(x_{1},\cdots ,g(y_{1},...,y_{m}),x_{i+m},\cdots ,x_{n})}$

where in the i-th position was replaced by. This is a picture of . This can be graphically represented as a composition of trees. ${\displaystyle x_{i}}$ ${\displaystyle g}$ ${\displaystyle P(m)\times P(n)\to P(m+n-1)}$

The identity operates as usual on : for everyone . ${\displaystyle I}$ ${\displaystyle f\in P(n)}$ ${\displaystyle I\circ _{k}f=f\circ _{k}I=f}$ ${\displaystyle 1\leq k\leq n}$

The following associative law applies to the composition:

${\displaystyle (f\circ _{1}g)\circ _{1}h=f\circ _{1}(g\circ _{1}h)}$

if one only looks at the composition in relation to the first variable. In general, more complex laws apply: Let , and , then: ${\displaystyle f\in P(n)}$ ${\displaystyle g\in P(m)}$ ${\displaystyle h\in P(l)}$

${\displaystyle (f\circ _{i}g)\circ _{j}h=(f\circ _{j}h)\circ _{i+l-1}g}$ For ${\displaystyle 1\leq j<i}$

${\displaystyle (f\circ _{i}g)\circ _{j}h=f\circ _{i}(g\circ _{j-i+1}h)}$ For ${\displaystyle i\leq j\leq m+i-1}$

${\displaystyle (f\circ _{i}g)\circ _{j}h=(f\circ _{j-m+1}h)\circ _{i}g}$ For ${\displaystyle j\geq i+m}$

These compositional rules also constitute the definition of non-symmetrical operads. In many applications there is symmetry with regard to the permutation of the input variables. One then defines symmetrical operads in which, after the effect of the permutation group, the two definition rules for the compositions are retained (effect of the identity operation and the above rules of associativity) and additional rules of equivariance:

Let be the symmetric group of n elements acting on P (n). So for , , , ${\displaystyle S_{n}}$ ${\displaystyle f\in P(n)}$ ${\displaystyle \sigma \in S_{n}}$ ${\displaystyle g\in P(m)}$ ${\displaystyle \tau \in P(m)}$

${\displaystyle \sigma f\circ _{i}\tau g=(\sigma \circ _{i}\tau )\,(f\circ _{i}g)}$

for and the block permutation in which the i-th element of is replaced by. Often, symmetric operads are simply referred to as operads. ${\displaystyle 1\leq i\leq n}$ ${\displaystyle \sigma \circ _{i}\tau }$ ${\displaystyle \sigma }$ ${\displaystyle \tau }$

For example, one can imagine functions on a real vector space for the elements of P (n) , but the elements P (n) can also be defined as mappings on topological spaces, chain complexes, polytopes (such as associate hedrons) or completely different objects, for which a composition of operators as above makes sense. It is also said that a symmetric operad can be defined in any symmetric monoidal category. ${\displaystyle P:V^{n}\to V}$ ${\displaystyle V}$

Examples

A simple example of a non-symmetric operad consists of the addition (A) and multiplication (M) of two numbers. The operations are elements of P (2). The composition of A and M is an element of P (3), explicitly:

${\displaystyle A\circ _{1}M(x,y,z)=x\cdot y+z}$

${\displaystyle A\circ _{2}M(x,y,z)=y\cdot z+x}$

${\displaystyle A\circ _{1}A(x,y,z)=A\circ _{2}A(x,y,z)=x+y+z}$

${\displaystyle M\circ _{1}M(x,y,z)=M\circ _{2}M(x,y,z)=x\cdot y\cdot z}$

${\displaystyle M\circ _{1}A(x,y,z)=(x+y)\cdot z=x\cdot z+x\cdot y}$

${\displaystyle M\circ _{2}A(x,y,z)=(y+z)\cdot x=y\cdot x+z\cdot x}$

Are not included , and , but they are included if one of the inputs permutations permits (symmetrical Operade). ${\displaystyle x\cdot z+y}$ ${\displaystyle (x+z)\cdot y=x\cdot y+z\cdot y}$

An important example is the Operade smaller discs (little disk operade). One looks at n different non-overlapping circles in a large circle, all of which are numbered. They form the element The composition of and consists in that P (k) is inserted in P (n) in place of the i-th disc and then renumbered. For example, if P (2) consists of disks 1,2 and is inserted in P (3) (consisting of disks (1,2,3) = (a, b, c)) in the second position ( ), then consists the new figure from the disks (a, 1,2, c) with the new numbering (1,2,3,4). Since the small slices can be permuted, it is also a symmetrical operad. Instead of small disks, cubes are sometimes also considered. ${\displaystyle P(n)}$ ${\displaystyle P(n)\circ _{i}P(k)}$ ${\displaystyle P(n)}$ ${\displaystyle P(k)}$ ${\displaystyle P(3)\circ _{2}P(2)}$

Endomorphism Operad and Algebra of Operads

An important example is the operade of endomorphisms , the set of all multilinear mappings (let V be a vector space). The composition is given by with , which maps by, the output is taken from g as i-th input of f. The input is permuted by the effect of the symmetrical group. The endomorphism operad is often used to represent abstract operads. One then speaks of a P-algebra of an operad P. Algebras of operads are related to operads in the same way as representations of groups in groups. ${\displaystyle End_{V}(n)}$ ${\displaystyle V^{n}\to V}$ ${\displaystyle f\circ _{i}g}$ ${\displaystyle f\in End_{V}(n)}$ ${\displaystyle g\in End_{V}(m)}$ ${\displaystyle V^{n+m-1}\to V}$

Applications in topology

Originally operads were introduced for a homotopy-invariant characterization of loop spaces. For loops with a fixed base, the associated operade is given by polytopes, the so-called association drones. For example, with four loops (a, b, c, d) the associahedron consists of a pentagon, the corners of which correspond to the loop combinations (ab) (cd), ((ab) c) d), (a (bc)) d, a ((bc) d) and a (b (cd)) correspond. ${\displaystyle K_{4}}$

A space is a topological space with a homotopy-coherent set of mappings ${\displaystyle A_{\infty }}$ ${\displaystyle Y}$

${\displaystyle f_{n}:K_{n}\times Y^{n}\to Y}$

so that Y is an algebra over the (non-symmetric) operad . The A stands for associative and means that the number of images, provided with the parameter above , is arbitrarily high. Then the following applies: ${\displaystyle K=\{K_{n}\}}$ ${\displaystyle \infty }$ ${\displaystyle n}$

A contiguous space of the homotopy type of a CW complex has the homotopy type of a loop space for a space if and only if Y is a space. ${\displaystyle \Omega X}$ ${\displaystyle X}$ ${\displaystyle A_{\infty }}$

Applications in mathematical physics

Operads found applications in mathematical physics in the 1990s and thereafter, for example in topological quantum field theories and string theory . There, Riemannian surfaces with dots and markings play a role and the use of the small slice operade leads to modular operades. In the string field theory of open strings, the analog of spaces plays a role for chain complexes, the -algebra, for closed strings and deformation quantization, the -algebra, where L stands for Lie groups. ${\displaystyle A_{\infty }}$ ${\displaystyle A_{\infty }}$ ${\displaystyle L_{\infty }}$

Another application is Maxim Kontsevich's proof that every classical mechanical system can be deformed into a quantum mechanical system (deformation quantization of Poisson manifolds ). More precisely, the multiplication is deformed on the associated observables.

On the one hand, the small disk operade is viewed on chain complexes instead of on topological spaces. Let the new operade be C. On the other hand, consider Hochschild Ko-chains on the set of observables O. This gives the operad H of the Hochschild Ko-chains on O, that is, the functions with n observables as input and one observable as output. They are linear in input. A conjecture by Pierre Deligne says that H is an algebra over the operade C. This has since been proven by Kontsevich and others, with Kontsevich's theorem about the existence of the quantum mechanical deformation of classical systems followed.

literature

• Martin Markl, Steve Shnider, James Stasheff : Operads in Algebra, Topology and Physics, Providence, American Mathematical Society, 2002
• JP May: The Geometry of Iterated Loop Spaces, Berlin, Springer-Verlag, 1972
• Jean-Louis Loday , Bruno Vallette: Algebraic Operads, Springer, Grundlehren der Mathematischen Wissenschaften 346, Springer 2012
• James Stasheff: What Is… an Operad ?, Notices of the American Mathematical Society, Volume 51, June / July 2004, pp. 630–631, pdf
• Jean-Louis Loday: Le renaissance de l 'operads, Séminaire Bourbaki 792, 1994/95, numdam
• Bruno Vallette: Algebra + Homotopy = Operad, Arxiv 2012

Web links

• Krähmer, From computer algorithms to quantum field theory: an introduction to operads , Oberwolfach, Snapshots in modern mathematics
• Operad in ncatlab
• What is an Operad? , Part 1, part 2 , math3ma

Individual evidence

1. ^ Boardman, Vogt, Homotopy Invariant Algebraic Structures on Topological Spaces, Lecture Notes in Mathematics 347, Springer 1973
2. ↑ May, The Geometry of Iterated Loop Spaces, Lecture Notes in Mathematics 271, Springer 1972
3. ↑ Victor Ginzburg, Mikhail Kapranov: Koszul duality for operads , Duke Mathematical Journal, Vol 76, 1994, pp 203-272.
4. ↑ M. Kontsevich, Y. Soibelman, Deformations of algebras over operads and the Deligne conjecture, Conference Moshe Flato 1999, Volume 1, Kluwer 2000, pp. 255-307