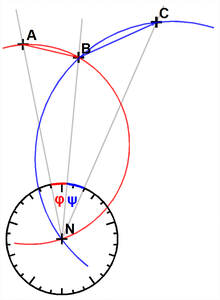
Backward cut
The plane reverse cut is a trigonometric method for land surveying (see geodesy ). The coordinates of a new point N are determined by three points A, B and C with known coordinates, if the horizontal angles ANB = φ and BNC = ψ (viewed from N) are known.
These angles can be calculated from the three direction measurements at new point N to points A, B, C. The solution is obtained by cutting the two peripheral angular circles (see peripheral angle set) with the angles φ (above the chord AB) and ψ (above the chord BC).
inventor
The task of the plane reverse cut is also called Pothenot's task after Laurent Pothenot ; however, before this, Willebrord van Roijen Snell (Snellius) published a solution. That is why some authors speak of the Snellius-Pothenot problem . Numerical solution methods for this task have also been proposed by Cassini , Abraham Gotthelf Kästner , Collins , Carl Friedrich Gauß and Ansermet , among others .
Dangerous circle
The backward step fails if the points A, B, C, N lie on a circle. Then the two peripheral angular circles lie on top of one another and do not result in a point of intersection. In the figure on the right, point A is almost on the arc of CBN. Measurement errors smear the exact position of the circles. Instead of a clear point of intersection at N, one obtains an intersection area N'-N 'in a graphic construction. This case is called a dangerous circle .
Experienced geodesists will avoid this arrangement (specifically, the angle between the two circles should be at least 30 °), since the measurement errors to be expected there cause location errors of a few centimeters to meters.