Round section (truss)

A round cut (also round cut method , node process , node method , node interface process or node equilibrium process ) is a calculation method of the Structural Analysis for sectional reactions and is mainly used in trusses used. In the case of a round cut, a knot is cut out “all around” in the framework in order to observe the forces that are short-circuited at this knot. In an ideal framework, only normal forces act on the bars connected to the node , which are often referred to as bar forces in this context.

Calculation method

Every knot must be in balance. For this one uses the equilibrium of forces of each vector component as an aid . The (vectorial) equilibrium of moments around a single ideal truss node is assumed, since according to theory, all members have only normal forces whose line of action lies in the member axis. According to theory, these lines of action go exactly through the articulated knot, so the sum of all moments around the knot is zero. The following applies to 2-D and 3-D trusses: there is a linear, independent force equilibrium condition for each dimension. ${\displaystyle \sum {\vec {F}}_{i}={\vec {0}}}$

The framework would have to be verified in the deformed position with the associated bar angles, since it is there (and only there) in equilibrium. Since the rod axis rotation angles in practical building examples usually remain negligibly small (in terms of amount) (| φ (x) | ≤0.1), one can generally calculate without any problems with the planned rod angles and rod lengths, as these differ only slightly from the actual rod angles and rod lengths distinguish.

2D

The perimeter method is usually taught for the special case of a flat framework that has a horizontal and vertical direction. Here you can cut out any knot, regardless of how many unknown and known forces act on this knot. The vectorial equilibrium of forces is usually achieved with two scalar, linearly independent equilibrium conditions

• Sum of horizontal forces equal to zero and ${\displaystyle \sum H~=~0}$
• Sum of the vertical forces is zero ${\displaystyle \sum V~=~0}$

specified. Every statically determined ideal framework can only be solved with a round section, the support forces can also be calculated with it, but it is usually easier to determine the support reactions in advance. For the calculation of a truss, however, a combination of round cut and knight cut is often used in order to obtain equations that are as independent as possible and thus systems of equations that are easy to solve. If only up to two forces of a node are unknown whose lines of action are not parallel, each of these forces can be calculated with a one-dimensional, independent system of equations by considering the sum of the forces in any direction that is orthogonal to all other unknown forces of this node .

Zero bars in 2D

Since the nodes in an ideal framework are idealized as central groups of forces , the determination of the zero rods is based on the consideration that the forces are in equilibrium. Three forces that are not equal to zero can only be in equilibrium in a flat central force group if no two of the three forces are collinear with one another. The rules for zero members are thus:

1. If two bars are connected to an unloaded node that are not in the same direction (unloaded double bar), both bars are zero bars.
2. If two (non-collinear) bars are connected to a loaded node and the external force acts in the direction of one bar, the other bar is a zero bar in the theory of the I order (equilibrium in the undeformed position).
3. If three bars are connected to an unloaded node, two of which are in the same direction, the third bar is a zero bar in the theory I order (equilibrium in the undeformed position).

Simple example

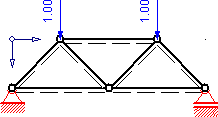
A statically determined framework with horizontal bars and bars at an angle of ± π / 4 (≙ ± 45 °).

The forces can be any multiple of 1  Newton . Due to static symmetry conditions it follows:

Since it is a statically determined framework, it is advantageous to calculate the four unknown support forces (one vertical and two horizontal forces as well as a restraint moment) using external (global) equilibrium:

The support moment in the upper flange results in zero by identifying the transverse force of the upper flange with zero, since there is no vertical support force, the moment at the joint is zero and, due to the differential relationship between moment and transverse force, the moment is constant with a transverse force equal to zero .

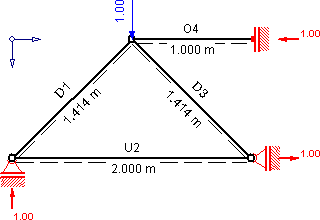
Introduction of member designations:

Cut out any knot. In order to keep the computational effort low, it is advantageous to choose a node with a maximum of two unknown forces that are not parallel. (The upper node would not be suitable because it has three as yet unknown bar forces.) To keep it clear, the normal force is often called the same as the bar name, which is not completely mathematically correct. The correct spelling for z. B. the normal force in member D1 could be: N_ {D1}.

Node1

Take the left support, for example, where two non-parallel, unknown bar forces act. ΣH = 0 would contain two unknowns and lead to D1 + √ (2) ⋅U2 = 0, with which a bar force could not be determined immediately. On the other hand, at =V = 0 (orthogonal to the lower chord U1), the diagonal D1 appears as the only unknown. ΣV = 0 rewritten as ΣVnachOben = ΣVnachBoden leads to: 1⋅ [N] + D1⋅sin (45 °) = 0 through transformation, D1 = -√ (2) ⋅ [N]. With ΣVto the right = ΣVto the left it follows: (√ (2) ⋅ [N]) ⋅cos (45 °) = U1, so that U1 = + 1⋅ [N]. In order not to forget a sign, it is advisable to add a sign even for positive values.

Node2

Now only the diagonal D2 and the top flange O4 are unknown. You can then D2 z. B. calculate with ΣV = 0 at the (lower) symmetry node and learn that it is a zero rod, since apart from D2 no other vertical forces act on the node. In order to check the correctness of the previous calculation on a random basis, you can also calculate nachHtoRight = ΣHtoLeft at the node, the result is 1⋅ [N] = 1⋅ [N] and thus a true statement.

Node3

Now there is only one truss knot where you can still make a round cut, namely the knot above. If the calculation is correct, ΣV = 0 leads to a true statement (0 = D1⋅sin (45 °) + 1⋅ [N]). For the equilibrium it is irrelevant whether it is an external action, a bar force or a support force, so it is treated in the same way. With ΣHto the right = ΣHto the left it follows: O4 = D1⋅cos (45 °) by inserting O4 = -1⋅ [N]

This results in the following for the entire framework:
D1 = -√ (2) ⋅ [N]
U2 = 1⋅ [N]
D3 = ± 0
O4 = -1⋅ [N]
U5 = U2 = 1⋅ [N]
D6 = D3 = ± 0
D7 = D1 = -√ (2) ⋅ [N]

Delimitation of the term

Multiple knots

A round cut could easily be extended by cutting out several nodes and then looking at the balance of forces. However, this is usually referred to as a knight cut , even if it also takes the balance of moments into account. A round cut can be viewed as a special case of the knight cut.

Moment equilibrium

In principle, it would be possible to set up the equation systems for each perimeter using only conditions of equilibrium of moments. In principle, an equilibrium of forces is nothing other than an equilibrium of moments of a point that is infinitely far away. In the case of an ideal truss node, however, it makes no sense to consider the moments around the node itself, as they do not allow any statement about the member axis forces. A sensible choice of points would have to be linearly independent of nodes and all other "observation points" in order to be able to set up a new linearly independent equation with every moment equilibrium.

literature

• Bernhard Pichler, Josef Eberhardsteiner: Structural Analysis VO - LVA-Nr . 202.065 . Ed .: E202 Institute for Mechanics of Materials and Structures - Faculty of Civil Engineering, TU Vienna. SS 2017 edition. TU Verlag, Vienna 2017, ISBN 978-3-903024-41-0 , 6.3 Nodal equilibrium method (round cut method) (516 pages, tuverlag.at - first edition: 2012).
• Kalliauer J .: Examination questions for Mechanics 1 (Vienna University of Technology). (PDF) Kalliauer J., June 2012, pp. 35–36 , accessed on November 6, 2015 . 
• Christian Spura: Technical Mechanics 1. Stereostatics . Springer, Wiesbaden 2016, ISBN 978-3-658-14984-0 .

See also

• analogous procedure for bending bars: cutting reaction
• alternative method for trusses: knight cut
• a 1-D truss is commonly referred to as axially stressed Gerber carrier designated

Individual evidence

1. ^ Bernhard Pichler, Josef Eberhardsteiner: Structural Analysis VO LVA-Nr . 202.065 . Ed .: E202 Institute for Mechanics of Materials and Structures - Faculty of Civil Engineering, TU Vienna. SS 2017 edition. TU Verlag, Vienna 2017, ISBN 978-3-903024-41-0 , 2.4 Linear geometric relationships (516 pp., Tuverlag.at - first edition: 2012). Structural Analysis VO LVA-Nr. 202.065 ( Memento of the original from July 17, 2017 in the Internet Archive ) Info: The archive link was inserted automatically and has not yet been checked. Please check the original and archive link according to the instructions and then remove this notice.