Segre's Theorem (Projective Geometry)

To define a finite oval: tangent, secant, is the order of the projective plane (number of points on a straight line −1) ${\displaystyle t}$ ${\displaystyle s_{1},...s_{n}}$ ${\displaystyle n}$

The set of Segre , named after the Italian mathematician Beniamino Segre , is in the projective geometry the statement:

• In a finite Pappus projective plane of odd order, each oval is a conic section .

The statement was suspected in 1949 by the Finnish mathematicians G. Järnefelt and P. Kustaanheimo and their proof was published in 1955 by B. Segre.

A finite Pappus projective plane can be imagined in inhomogeneous coordinates like the real projective plane described, only that instead of the real numbers a finite field is used. Odd order means that is odd. An oval is a circle-like curve (see below): A straight line intersects at most twice and there is exactly one tangent at each point. The standard examples of ovals are the non-degenerate (projective) conic sections . ${\displaystyle K}$ ${\displaystyle |K|=n}$

Segre's theorem is very important for finite ovals, since in the Pappus odd case there can be no other ovals apart from the conic sections. In contrast to straight pappus planes: Here there are ovals that are not conic sections (see Qvist's theorem ). In infinite pappus planes there are ovals that are not conic sections. In the real world, one only has to smoothly join a semicircle with a suitable semiellipse.

The proof of the theorem for the proof that the given oval is a conic section is carried out with the help of the 3-point degeneration of Pascal's theorem . The property that is typical for bodies of odd order, that the product of all elements that are not 0, is equal to −1, is used.

Definition of an oval

→ Main article : Oval (projective geometry)

• A set of points in a projective plane is called an oval , if ${\displaystyle {\mathfrak {o}}}$

(1) Any straight line hits a maximum of 2 points. If is, is called passer , if is, is called tangent and if is, is called secant . ${\displaystyle g}$ ${\displaystyle {\mathfrak {o}}}$
${\displaystyle |g\cap {\mathfrak {o}}|=0}$ ${\displaystyle g}$ ${\displaystyle |g\cap {\mathfrak {o}}|=1}$ ${\displaystyle g}$ ${\displaystyle |g\cap {\mathfrak {o}}|=2}$ ${\displaystyle g}$

(2) For every point there is exactly one tangent , i. H. . ${\displaystyle P\in {\mathfrak {o}}}$ ${\displaystyle t}$ ${\displaystyle t\cap {\mathfrak {o}}=\{P\}}$

For finite projective planes (i.e. the set of points and set of lines are finite)

• In a projective plane of order (i.e. every straight line contains points), a set is an oval if and only if is and no three points are collinear (on a straight line). ${\displaystyle n}$ ${\displaystyle n+1}$ ${\displaystyle {\mathfrak {o}}}$ ${\displaystyle |{\mathfrak {o}}|=n+1}$ ${\displaystyle {\mathfrak {o}}}$

3-point degeneration of Pascal's theorem

for the proof, the tangent is in ${\displaystyle g_{\infty }}$ ${\displaystyle P_{3}}$

Sentence:

Let it be an oval in a Pappus projective plane of the characteristic . is a non-degenerate conic section if and only if the following statement (P3) applies: ${\displaystyle {\mathfrak {o}}}$ ${\displaystyle \neq 2}$
${\displaystyle {\mathfrak {o}}}$

(P3): Is any triangle and the tangent in at , so are the points ${\displaystyle P_{1},P_{2},P_{3}}$ ${\displaystyle {\mathfrak {o}}}$ ${\displaystyle {\overline {P_{i}P_{i}}}}$ ${\displaystyle P_{i}}$ ${\displaystyle {\mathfrak {o}}}$

${\displaystyle P_{4}:={\overline {P_{1}P_{1}}}\cap {\overline {P_{2}P_{3}}},\ P_{5}:={\overline {P_{2}P_{2}}}\cap {\overline {P_{1}P_{3}}},\ P_{6}:={\overline {P_{3}P_{3}}}\cap {\overline {P_{1}P_{2}}}}$

collinear.

To prove the 3P Pascal theorem

Proof:

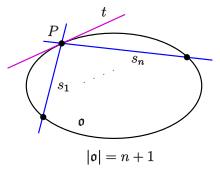
The projective plane is shown in inhomogeneous coordinates over the body in such a way that the tangent in , the x-axis is the tangent in the point and contains the point . Furthermore, let (see picture) the oval can be described with the help of a function as follows: ${\displaystyle K}$ ${\displaystyle P_{3}=(0),\;g_{\infty }}$ ${\displaystyle P_{3},\ (0,0)\in {\mathfrak {o}}}$ ${\displaystyle (0,0)}$ ${\displaystyle {\mathfrak {o}}}$ ${\displaystyle (1,1)}$ ${\displaystyle P_{1}=(x_{1},y_{1}),\;P_{2}=(x_{2},y_{2})\ .}$
${\displaystyle {\mathfrak {o}}}$ ${\displaystyle f:K\mapsto K}$

${\displaystyle {\mathfrak {o}}=\{(x,y)\in K^{2}\;|\;y=f(x)\}\ \cup \{(\infty )\}\;.}$

The tangent at the point is given by the equation using a function ${\displaystyle (x_{0},f(x_{0}))}$ ${\displaystyle f'}$

${\displaystyle y=f'(x_{0})(x-x_{0})+f(x_{0})}$

described. It then applies (see picture)

${\displaystyle P_{5}=(x_{1},f'(x_{2})(x_{1}-x_{2})+f(x_{2}))\;}$ and ${\displaystyle P_{4}=(x_{2},f'(x_{1})(x_{2}-x_{1})+f(x_{1}))\;.}$

I: If is a non-degenerate conic is and and is expected to light that are collinear (see parable ). ${\displaystyle {\mathfrak {o}}}$ ${\displaystyle f(x)=x^{2}}$ ${\displaystyle f'(x)=2x}$ ${\displaystyle P_{4},P_{5},P_{6}}$

II: If there is an oval with property (P3) , the slope of the straight line is equal to the slope of the straight line , i.e. H. it is ${\displaystyle {\mathfrak {o}}}$ ${\displaystyle {\overline {P_{4}P_{5}}}}$ ${\displaystyle {\overline {P_{1}P_{2}}}}$

${\displaystyle f'(x_{2})+f'(x_{1})-{\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}={\frac {f(x_{2})-f(x_{1})}{x_{2}-x_{1}}}}$ and therefore applies

(i): for everyone . ${\displaystyle (f'(x_{2})+f'(x_{1}))(x_{2}-x_{1})=2(f(x_{2})-f(x_{1}))}$ ${\displaystyle x_{1},x_{2}\in K}$

With you get ${\displaystyle f(0)=f'(0)=0}$

(ii): and with follows ${\displaystyle f'(x_{2})x_{2}=2f(x_{2})}$ ${\displaystyle f(1)=1}$

(iii): ${\displaystyle f'(1)=2\;.}$

From (i) and (ii) results

(iv): and with (iii) finally ${\displaystyle f'(x_{2})x_{1}=f'(x_{1})x_{2}}$

(v): for everyone . ${\displaystyle f'(x_{2})=2x_{2}}$ ${\displaystyle x_{2}\in K}$

From (ii) and (v) it follows

${\displaystyle f(x_{2})=x_{2}^{2},\;x_{2}\in K}$.

So is a non-degenerate conic section. ${\displaystyle {\mathfrak {o}}}$

Comment:

1. Property (P3) is fulfilled in Pappusian planes of characteristic 2 for all ovals with a node N (all straight lines through N are tangents). Also for ovals that are not conic sections.
2. The 3-point Pascal theorem is also valid for ovals in infinite Pappus planes over bodies of the characteristic . ${\displaystyle \neq 2}$

Statement and proof of Segre's theorem

Sentence:

An oval in a finite pappus projective plane of odd order is a non-degenerate conic section. ${\displaystyle {\mathfrak {o}}}$

3-point degeneration of Pascal's theorem, for which is proof ${\displaystyle g_{\infty }={\overline {P_{2}P_{3}}}}$

Segre's theorem: for proof

Proof:

As a proof it is shown that the oval fulfills the property (P3) of the 3-point degeneration of Pascal's theorem (see above).

So be any triangle on and as explained in (P3) . The Pappus plane is represented in inhomogeneous coordinates over a finite body in such a way that and is the intersection of the tangents in and . The oval can be represented with the help of a bijective function : ${\displaystyle P_{1},P_{2},P_{3}}$ ${\displaystyle {\mathfrak {o}}}$ ${\displaystyle P_{4},P_{5},P_{6}}$ ${\displaystyle K}$ ${\displaystyle P_{3}=(\infty ),\;P_{2}=(0),\;P_{1}=(1,1)}$ ${\displaystyle (0,0)}$ ${\displaystyle P_{2}}$ ${\displaystyle P_{3}}$ ${\displaystyle {\mathfrak {o}}}$ ${\displaystyle f:K^{*}:=K\cup \setminus \{0\}\mapsto K^{*}}$

${\displaystyle {\mathfrak {o}}=\{(x,y)\in K^{2}\;|\;y=f(x),\;x\neq 0\}\;\cup \;\{(0),(\infty )\}\;.}$

If now , then the slope of the secant Da is both and a bijection of on , and a bijection of on is, where the slope of the tangent is in, holds for ${\displaystyle P=(x,y),\;x\in K\setminus \{0,1\}}$ ${\displaystyle m(x)={\tfrac {f(x)-1}{x-1}}}$ ${\displaystyle {\overline {PP_{1}}}\;.}$ ${\displaystyle x\mapsto f(x)-1}$ ${\displaystyle x\mapsto x-1}$ ${\displaystyle K\setminus \{0,1\}}$ ${\displaystyle K\setminus \{0,-1\}}$ ${\displaystyle x\mapsto m(x)}$ ${\displaystyle K\setminus \{0,1\}}$ ${\displaystyle K\setminus \{0,m_{1}\}}$ ${\displaystyle m_{1}}$ ${\displaystyle P_{1}}$ ${\displaystyle K^{**}:=K\setminus \{0,1\}\;:}$

${\displaystyle \prod _{x\in K^{**}}(f(x)-1)=\prod _{x\in K^{**}}(x-1)=1\quad {\text{und}}\quad m_{1}\cdot \prod _{x\in K^{**}}{\frac {f(x)-1}{x-1}}=-1\;.}$

(Note: For the following applies: ) So ${\displaystyle K^{*}:=K\setminus \{0\}}$ ${\displaystyle \displaystyle \prod _{k\in K^{*}}k=-1\;.}$

${\displaystyle -1=m_{1}\cdot \prod _{x\in K^{**}}{\frac {f(x)-1}{x-1}}=m_{1}\cdot {\frac {\displaystyle \prod _{x\in K^{**}}(f(x)-1)}{\displaystyle \prod _{x\in K^{**}}(x-1)}}=m_{1}\;.}$

Since the slopes of and the tangent are both , it results . This is true for every triangle . ${\displaystyle {\overline {P_{5}P_{6}}}}$ ${\displaystyle {\overline {P_{1}P_{1}}}}$ ${\displaystyle -1}$ ${\displaystyle {\overline {P_{1}P_{1}}}\cap {\overline {P_{2}P_{3}}}=P_{4}\in {\overline {P_{5}P_{6}}}}$ ${\displaystyle P_{1},P_{2},P_{3}\in {\mathfrak {o}}}$

So the property (P3) of 3-point degeneracy of Pascal's theorem applies and the oval is a non-degenerate conic section.

Web links

• E. Hartmann: Planar Circle Geometries, an Introduction to Moebius, Laguerre and Minkowski Planes. Script, TH Darmstadt (PDF; 891 kB), p. 41.

literature

• P. Dembowski : Finite Geometries. Springer-Verlag, 1968, ISBN 3-540-61786-8 , p. 149
• B. Segre : Ovals in a finite projective plane , Canad. Journal of Math. 7 (1955), pp. 414-416.
• G. Järnefelt & P. Kustaanheimo : An observation on finite geometries , The 11th Skandinaviske Matematikerkongress, Trondheim (1949), pp. 166–182.
• Albrecht Beutelspacher , Ute Rosenbaum: Projective geometry. 2nd Edition. Vieweg, Wiesbaden 2004, ISBN 3-528-17241-X , p. 162.

Individual evidence

1. ^ E. Hartmann: Planar Circle Geometries, an Introduction to Moebius, Laguerre and Minkowski Planes. Script, TH Darmstadt (PDF; 891 kB), p. 35.