Solitaire (board game)
Solitaire (also Solitaire, Steckhalma, Solohalma, Springer, Jumper, Nonnenspiel, Einsiedlerspiel ) is a board game for one person. The most widespread playing field is cross-shaped, and it is equipped with 32 stones on 33 fields. This game is also known as English Solitaire (picture).
Since the card game is also called Patience Solitaire , at least in the USA , the board game is more likely to be called Peg Solitaire or Sailor's Solitaire, in the USA it is also called Hi-Q after a well-known brand .
history

It is certain that the game was first known in France . It appears for the first time in 1697 on an engraving by Claude-Auguste Berey and was certainly played at the court of the Sun King . It is first mentioned in England in 1746.
The story of the "French nobleman in prison" comes from an English book from 1801, as John Beasley records in 1985 in the only specialist book on the subject, The Ins and Outs of Peg Solitaire . Beasley refers this story to the realm of "ineradicable fables", with correspondingly little success. Also, that it could have been invented overseas cannot be ruled out or verified. The English name Sailor's solitaire could suggest this.
In Switzerland, this board game is widely known as the "Amden Tubbeli Game". Amden is a village on the Walensee . Craftsmen in Amden make such board games.
Gottfried Wilhelm Leibniz valued the game and mentioned in a letter in 1710 that he had found his own variant for it.
One of the oldest printed game boards available is cross-shaped, has 45 fields and was manufactured by JC Wiegleb in 1779.
regulate
The point is to let one piece jump over exactly one tile next to it, which is then "deleted". Stones may only jump in rows and columns, but not diagonally. Only one stone should be left exactly in the middle of the board.
- Solitaire for two
The game can also be played in pairs, although this is rarely practiced. The opponents take turns moving. The loser is someone who can no longer jump.
Board variants

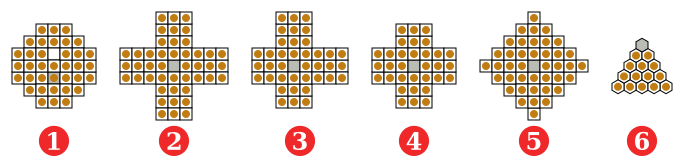
The most varied of board shapes occur: In addition to the most common fully symmetrical "English" solitaire (4) and the original shape, the "French" solitaire (1), there are different crosses, e.g. B. the German Wiegleb board with 45 fields from 1779 (2), crosses with arms of different lengths (3-3-2-2) (3), squares like the diamond with 41 fields (5), 6 × 6 and 8 × 8 boards (which of course cannot have a center field), 9 × 9 boards, triangular versions (most often with 15 fields; 6) and many more - star-shaped arrangements were also played.
For his research, George Bell in particular developed new special shapes, such as rhombuses, the mushroom-shaped mushroom board with 36 fields, and similar ones with 75 and 90 fields.
The English standard board (33 fields, Figure 4)
- The standard game consists of filling all fields except one with stones on a 33-inch board. The free space at the start of the game and the goal are usually in the middle ( d4 → d4 ).
- However, the game on this board can be solved from any starting constellation with a free field.
The French board (37 fields, Figure 1)
- The problem d4 → d4, "Free space ... middle, last stone ... middle" is proven not to be solvable on the 37-point board , which strongly suggests that this game originally also allowed diagonal moves (which also makes this problem solvable). In today's usual moves, two stones are left if only the midfield was free at the start of the game.
- Only three starting constellations (and their rotated and / or mirrored counterparts) can be played on this board down to a single remaining piece, namely the one with the free space on c1 or d3 or d6.
- Literature on this older board , known in France by the way as European , is significantly more sparse than on the 33rd.
Other versions of the game
- In some variants, certain target configurations are to be generated from a wide variety of starting configurations, for example a “pyramid” or a “cross” is to be dismantled or created.
- Gottfried Wilhelm Leibniz's special way of playing was to let the “holes” “jump” instead of the stones.
- Furthermore, the goal of symmetrical end positions can be a criterion for the course of the game.
Computer programs
Solutions can be found with the help of computer programs. A fundamentally well-suited method is " recursive backtracking ". If all possibilities are tried out systematically, then it can also be checked whether there is a solution from a certain starting position for a certain end position. Since only a small part of the stones are able to reach the target field as the last stone due to the special nature of the jumps (for example, this is only 4 stones in the English standard variant), the search can be accelerated many times over by pressing Each jump is checked whether the stones in question are still in play. If this is not the case, the current sequence can be canceled.
Since there are usually a large number of solutions for the same task, the final challenge is to find the solution with the fewest “pulls” (which means that the same stone has to jump several times in quick succession). The proven shortest possible solution for the standard game on the board of 33, d4 → d4, was already found in 1912 by game guru Ernest Bergholt : 18 “moves”, namely b4-d4, c6-c4, a5-c5, d5-b5 , f5-d5, e7-e5, e4-e6, c7-e7-e5, c3-c5, c1-c3, e2-e4-e6-c6-c4-c2, a3-a5-c5-e5, g3-e3 , d3-f3, g5-g3-e3, e1-c1-c3, b3-d3-f3-f5-d5-d3, d2-d4.
In 1999 the standard solitaire game was completely calculated on the computer and the entire solution space was thus accessible. The techniques used were: backtracking, exhaustive search, hashing, distributed computing, efficient storage of the board constellation, among other things by using symmetries.
In 2003 Jean-Charles Meyrignac and George Bell presented further programs for solving solitaire (game) tasks. Meyrignac has calculated 280 different solutions for the starting constellation “Free field = c1” on the 37-note board (and has proven that this task only requires 20 “moves”).
Note on the term "train"
It would make sense, as Jürgen Köller does, to only use "train" to designate what could also be called a train series or similar, and to always call the "individual train" just a jump , but the general usage is different (one thinks of Chess and other board games). In this article, only “train” in quotation marks means several consecutive jumps with the same stone. Bergholt's 18 “moves” naturally consist of 31 jumps, Meyrignac's 20 “moves” consist of 35 jumps.
proof
- ^ Beasley, 2003
- ↑ Strasser Helmut (2005), Solitaire: All symmetrical end positions
- ↑ Eichler, Jäger, Ludwig (c't 07/1999) Spielverderber, Solitaire solving with the computer
Web links
- http://mathematische-basteleien.de/solitaer.htm (Jürgen Köller)
- http://www.yogpielee.de - Page with 3 different, animated solutions for the standard board with 33 fields.