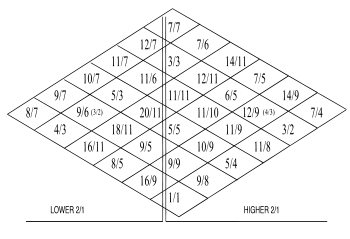
Tonality diamond

from Wikipedia, the free encyclopedia
This article or the following section is not adequately provided with supporting documents ( e.g. individual evidence ). Information without sufficient evidence could be removed soon. Please help Wikipedia by researching the information and including good evidence.

A tonality diamond is a music theory diagram . The diagram is mainly known through the work of Harry Partch .

Sound system

Harry Partch's tone system is based on Hermann von Helmholtz 's theory of tone sensations , after reading it, he rejected the tempered tone system and the major-minor dualism. In particular, one can perhaps speak of an extended version of Max Meyer's tonality diamond . This "diamond" generates - as Partch put it - "Otonalities" and "Utonalities" on its two diagonal axes: Otonalities (o = 'over', or 'Major') and Utonalities (u = 'under' or 'Moll') . These “Otonalities” and “Utonalities” go beyond the major and minor by including the 7th, 9th and 11th natural notes.

Partch starts from the following network of integer intervals , where 1/1 denotes the fundamental G of his system, 9/8 the major second A according to the natural tuning , 5/4 the pure major third B (about a twelfth tone lower than in the tempered system), 11/8 the 11th natural tone C sharp (about a quarter tone lower), 3/2 the perfect fifth D (slightly higher), 7/4 the natural seventh (about a sixth tone lower) etc. This is his "Otonality". Their values ​​can be read from the bottom left to the top right on the diagonal and start at different values ​​that are plotted on the opposite diagonal. This opposite diagonal from the bottom right to the top left includes the inversion of the values ​​and is called “Utonality” by Partch.

11-limit tonality diamond

In order to convert these numerical ratios (= interval ratios to "Identity" 1/1, i.e. our tone G) as pitch values in cents , this formula can be used:

You divide the numerical values, form the logarithm (base 10, on the calculator “log”) and multiply by 3986. So for 11/10 you get the cent value 165. The interval 11/10 is 165 cents above G. That is an interval between a small and a large second. 11/10 is like an 11th natural tone 11/8 above a fundamental tone, which is a natural third 4/5 (Partch writes an octave 8/5) below G (see the position on the diamond!), I.e. 11/8 ⋅ 4 / 5 = 11/10. The upward octave applies to all values ​​of the left half of his diamond and is due to the formation of the scales with these same proportions that Partch undertook. So on the keys of his "Chromelodeon", which is able to play the desired pitches in its purest form, the proportions of the diamond and all other added intervals are painted as numbers in all octaves! The intervals given in the “tonality diamond” are difficult to reproduce in our musical notation, as many tones differ greatly from the tempering. If in the following experiment we assume a perfect fifth notation (the perfect 3/2 fifth is only about 2 cents higher than the tempered one), thirds, septa and the 11th natural note must be indicated in order to indicate Partch's system with our notes. The "Otonality" on G looks like this in the 1st transcription example:

Harry Partch: 1. Transcription of the Otonality on G = lower line of the tonality diamond from bottom left to top right

The opposite diagonal from the bottom right to the top left, the "Utonality", is the exact reverse of the "Otonality" and reads as follows in the 2nd transcription example (we use the proportions from Partch's diamonds for the sake of clarity; actually, instead of 16 / 9 is better to write 8/9 than the inverse of 9/8; Partch did not do this either, since once the proportions were chosen, each signaled a pitch in all octaves for him ):

Harry Partch: 2. Transcription of the Utonality under G = bottom line of the tonality diamond bottom right to top left

As a sound example follows 1. "Otonality" on G, 2. "Utonality" under G, 3. Some changes between O and U tonalities with microtonal shades 

  Audio-Datei / Hörbeispiel Partch O- und Utonality?/i

All parallel diagonals produce either otonalities or tonalities on different transposition levels. We can make this clear in a third transcription, which first transcribes Partch's “Primary Tonalities” (those are those from the “Tonality Diamond”) and then adds his “Secondary Tonalities”, as well as individual pure fifths: These Partch mainly added to get a balanced microtonal scale.

The combinations of the indices are necessary in order to indicate the pure interval ratios of the 5th, 7th and 11th natural tones, even with tones that are already derived from these natural tone ratios. Take the combination of low-7 with high-5 as an example: The subscript 7 means that this is a natural sept, i.e. an interval 7/4 (about 1/6 tone lower). And the superscript 5 that appears at the same time indicates that a 4/5 interval is the starting point of this natural sept (approx. 1 / 12ton higher). Overall, this tone will be approx. 1/12 tone lower in the combination of the indices. A superscript 11 brings about 1 / 4ton up, a subscript 11 about 1 / 4ton down.

Harry Partch: 3. Transcription of all 43 tones of the Partch system

The composer liked to use the entire 43-note stock of Partch in linear form, on his kitharas or canons in arpeggio form. The transcription as a scale follows in the 4th example:

Harry Partch: 4. Transcription of all 43 tones of the Partch system as a scale

The “11-Limit” diamond with its “Primary Tonalities” is vividly embodied on the “Diamond Marimba” Partchs, a percussion instrument where the lamellae are arranged according to the tonality diamond, but in a different order: in thirds.

5-limit

3/2
5/4 6/5
1/1 1/1 1/1
8/5 5/3
4/3

7-limit

7/4
3/2 7/5
5/4 6/5 7/6
1/1 1/1 1/1 1/1
8/5 5/3 12/7
4/3 10/7
8/7

11-limit

11-limit tonality diamond

15-limit

15/8
7/4 5/3
13/8 14/9 3/2
3/2 13/9 7/5 15/11
11/8 4/3 13/10 14/11 5/4
5/4 11/9 6/5 13/11 7/6 15/13
9/8 10/9 11/10 12/11 13/12 14/13 15/14
1/1 1/1 1/1 1/1 1/1 1/1 1/1 1/1
16/9 9/5 20/11 11/6 24/13 13/7 28/15
8/5 18/11 5/3 22/13 12/7 26/15
16/11 3/2 20/13 11/7 8/5
4/3 18/13 10/7 22/15
16/13 9/7 4/3
8/7 6/5
16/15

swell