Turinggrad

In computability theory and mathematical logic , the Turing degree (also the degree of unsolvability ) of a set of natural numbers measures the algorithmic unsolvability of the set. The concept of the Turing degree is fundamental in computability theory, where sets of natural numbers are often viewed as decision problems ; the Turing degree of a set indicates how difficult the decision problem is for the set.

Two sets are Turing-equivalent if they have the same degree of unsolvability; every Turing degree is a set of Turing-equivalent sets, so that two sets are in different Turing degrees if and only if they are not Turing-equivalent. In addition, the Turing degrees are partially ordered in the following sense : If the Turing degree of a set is smaller than the Turing degree of a set , then every (unpredictable) procedure that correctly decides whether numbers are in can be converted calculably into a procedure that decides correctly whether numbers are in. In this sense, the Turing degree of a set corresponds to the degree of its algorithmic unsolvability. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle Y}$ ${\displaystyle X}$

The Turing degrees were introduced by Emil Leon Post in 1944 , and many basic results were demonstrated by Stephen Cole Kleene and Post in 1954 . The Turing degrees are the subject of intensive research to this day. Much evidence in this area uses an evidence technique known as the priority method.

Turing equivalence

In the following, the word set refers to subsets of natural numbers. A set is called Turing-reducible to a set , if there is an oracle-Turing machine that decides with the help of an oracle for whether a given number is in . The notation stands for: can be reduced to Turing. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle Y}$ ${\displaystyle X}$ ${\displaystyle X\leq _{T}Y}$ ${\displaystyle X}$ ${\displaystyle Y}$

Two sets and are called Turing-equivalent if they are Turing-reducible to one another. The notation stands for: and are Turing equivalent. The relation is an equivalence relation . ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X\equiv _{T}Y}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle \equiv _{T}}$

Turinggrad

A Turing degree is an equivalence class of the relation . The notation denotes the equivalence class that contains the set . The class of all Turing degrees is denoted by. ${\displaystyle \equiv _{T}}$ ${\displaystyle [X]}$ ${\displaystyle X}$ ${\displaystyle {\mathcal {D}}}$

The Turing degrees have a partial order . It is defined in such a way that if and only applies if . There is a Turing degree that contains exactly the decidable sets, and this degree is smaller than all others. It is denoted by (zero) because it is the smallest element of the partially ordered set . Turing degrees are usually denoted by bold type to distinguish them from quantities. Bold small letters etc. serve as variables for Turing degrees. ${\displaystyle \leq }$ ${\displaystyle [X]\leq [Y]}$ ${\displaystyle X\leq _{T}Y}$ ${\displaystyle \mathbf {0} }$ ${\displaystyle {\mathcal {D}}}$ ${\displaystyle \mathbf {a} ,\mathbf {b} }$

For all sets and is (pronounced join ) the union of the sets and . The Turing degree of is the supremum of the degrees and . This is an upper half lattice . The supremum of degrees and is denoted by. It is known that there is no association since there are pairs of degrees without an infimum. ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle X\oplus Y}$ ${\displaystyle \left\{2n\mid n\in X\right\}}$ ${\displaystyle \left\{2n+1\mid n\in Y\right\}}$ ${\displaystyle X\oplus Y}$ ${\displaystyle [X]}$ ${\displaystyle [Y]}$ ${\displaystyle {\mathcal {D}}}$ ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {b} }$ ${\displaystyle \mathbf {a} \cup \mathbf {b} }$ ${\displaystyle {\mathcal {D}}}$

For any set denotes the set of indexes by oracle machines that hold on to their own index as input when using as an oracle. The set is called the Turing jump of . The Turing jump of a degree is the degree ; this is well defined since it follows. An important example is the degree of the hold problem . ${\displaystyle X}$ ${\displaystyle X^{\prime }}$ ${\displaystyle X}$ ${\displaystyle X^{\prime }}$ ${\displaystyle X}$ ${\displaystyle [X]}$ ${\displaystyle \left[X^{\prime }\right]}$ ${\displaystyle X^{\prime }\equiv _{T}Y^{\prime }}$ ${\displaystyle X\equiv _{T}Y}$ ${\displaystyle \mathbf {0} ^{\prime }}$

Basic properties of the Turing grades

• Every Turing degree is countably infinite , that is, it contains exactly sets. ${\displaystyle \aleph _{0}}$

• There are (see Beth function ) different degrees of Turing. ${\displaystyle \beth _{1}}$

• The strict inequality applies to each degree . ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {a} <\mathbf {a} ^{\prime }}$

• For each degree the set of degrees is at most countable . The amount of degrees above has power . ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {a} }$ ${\displaystyle \beth _{1}}$

Structure of the Turing degrees

The structure of the Turing degrees has been intensively researched. The following list is just a few of the many known results. In general, it can be concluded from the known results that the structure of the Turing degrees is very complicated.

Order properties

• There are minimal degrees. A degree is called minimal if it is unequal and there is no degree between and . Thus the order of the degrees is not tight . ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {0} }$ ${\displaystyle \mathbf {0} }$ ${\displaystyle \mathbf {a} }$

• For every degree unequal there is a degree that cannot be compared with . ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {0} }$ ${\displaystyle \mathbf {b} }$ ${\displaystyle \mathbf {a} }$

• There are Turing degrees that are not comparable to one another. ${\displaystyle \beth _{1}}$

• There are pairs of degrees with no infimum. So there is no association. ${\displaystyle {\mathcal {D}}}$

• Every countable partial order can be embedded in the Turing degrees.

• No infinite, strictly ascending series of degrees has a supremum.

Properties of the jump operator

• For each grade there is a grade between and . There is even a countably infinite series of pairs of incomparable degrees between and . ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {a} ^{\prime }}$ ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {a} ^{\prime }}$

• A degree has the form for if and only if applies. ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {b} ^{\prime }}$ ${\displaystyle \mathbf {b} }$ ${\displaystyle \mathbf {0} <\mathbf {a} }$

• For every degree there is a degree , so and . Such a grade is called low relative to . ${\displaystyle \mathbf {a} }$ ${\displaystyle \mathbf {b} }$ ${\displaystyle \mathbf {a} <\mathbf {b} }$ ${\displaystyle \mathbf {a} ^{\prime }=\mathbf {b} ^{\prime }}$ ${\displaystyle \mathbf {b} }$ ${\displaystyle \mathbf {a} }$

• There is an infinite series of degrees, so for everyone . ${\displaystyle \left(\mathbf {a} _{i}\right)_{i}}$ ${\displaystyle \mathbf {a} _{i+1}^{\prime }\leq \mathbf {a} _{i}}$ ${\displaystyle i}$

Logical properties

• Simpson (1977) showed that the theory of the first predicate logic stage in the language , or many-one equivalent to the theory of natural numbers in the second-order logic is. ${\displaystyle {\mathcal {D}}}$ ${\displaystyle \left\langle {\leq },{=}\right\rangle }$ ${\displaystyle \left\langle {\leq },{\cdot }^{\prime },{=}\right\rangle }$

• Shore and Slaman (1999) showed that the jump operator in the structure of degrees in first-order logic can be defined with language . ${\displaystyle \left\langle {\leq },{=}\right\rangle }$

Structure of the recursively enumerable Turing degrees

This finite association cannot be embedded in the recursively enumerable degrees.

A degree is called recursively enumerable if it contains a recursively enumerable set . Every recursively enumerable degree is less than or equal to , but not every degree lower than that is recursively enumerable. ${\displaystyle \mathbf {0} ^{\prime }}$ ${\displaystyle \mathbf {0} ^{\prime }}$

• ( Theorem from Friedberg and Muchnik , 1956) There are recursively enumerable degrees between and . ${\displaystyle \mathbf {0} }$ ${\displaystyle \mathbf {0} ^{\prime }}$

• ( GE Sacks , 1964) The recursively enumerable degrees are dense, that is, between two recursively enumerable degrees there is always a third recursively enumerable degree.

• (AH Lachlan, 1966a and CEM Yates, 1966) There are two recursively enumerable degrees that do not have an infimum in the recursively enumerable degrees.

• (AH Lachlan, 1966a and CEM Yates, 1966) There are a pair of recursively enumerable degrees unequal whose infimum is. ${\displaystyle \mathbf {0} }$ ${\displaystyle \mathbf {0} }$

• (SK Thomason, 1971) Every finite distributive lattice can be embedded in the recursively enumerable degrees. It is even possible to embed countable boolean algebra without atoms in such a way that suprema and infima are preserved.

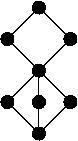
• (AH Lachlan and RI Soare , 1980) Not all finite lattices can be embedded in the recursively enumerable degrees, so that suprema and infima are preserved. In particular, the association shown on the right cannot be embedded.

• (AH Lachlan, 1966b) There is no pair of recursively enumerable degrees whose infimum is and whose supremum is ${\displaystyle \mathbf {0} }$ ${\displaystyle \mathbf {0} ^{\prime }}$

• ( LA Harrington and TA Slaman , see Nies, Shore, and Slaman (1998)) The theory of recursively enumerable degrees in language in first order logic is many-one equivalent to the theory of arithmetic in first order logic. ${\displaystyle \left\langle \mathbf {0} ,{\leq },{=}\right\rangle }$

literature

Introductions

• SB Cooper: Computability Theory. Chapman & Hall / CRC, 2004, ISBN 1-58488-237-9 .
• Nigel Cutland: Computability, An introduction to recursive function theory. Cambridge University Press, 1980, ISBN 0-521-29465-7 .
• Klaus Heidler, Hans Hermes, Friedrich-K. Reminder: recursive functions. Mannheim - Vienna - Zurich 1977.
• Hans Hermes : Enumerability - Decidability - Calculability. Introduction to the theory of recursive functions . Berlin / Göttingen / Heidelberg 1961. (2nd edition. 1971, as Heidelberg paperback).
• Stephen Kleene : Introduction to Metamathematics. North-Holland, 1952, ISBN 0-7204-2103-9 .
• Michael Sipser : Introduction to the Theory of Computation . PWS Publishing, 1997, ISBN 0-534-94728-X . Part Two: Computability Theory, Chapters 3-6, pp. 123-222.

Special works

• Piergiorgio Odifreddi : Classical Recursion Theory . North-Holland 1989, ISBN 0-444-87295-7 .
• P. Odifreddi: Classical Recursion Theory, Volume II. Elsevier, 1999, ISBN 0-444-50205-X .
• Hartley Rogers: Theory of recursive functions and effective computability . McGraw-Hill, 1967.
• G. Sacks: Higher Recursion Theory. Springer-Verlag, 1990, ISBN 3-540-19305-7 .
• RI Soare: Recursively Enumerable Sets and Degrees. Perspectives in Mathematical Logic. Springer-Verlag, 1987, ISBN 0-387-15299-7 .

Research papers

• Stephen Cole Kleene, Emil L. Post: The upper semi-lattice of degrees of recursive unsolvability . In: Annals of Mathematics. Second series . tape 59 , no. 3 , 1954, ISSN  0003-486X , pp. 379-407 , doi : 10.2307 / 1969708 , JSTOR : 1969708 .
• AH Lachlan: Lower Bounds for Pairs of Recursively Enumerable Degrees . In: Proceedings of the London Mathematical Society . tape 3 , no. 1 , 1966, p. 537 .
• AH Lachlan: The impossibility of finding relative complements for recursively enumerable degrees . In: J. Symb. Logic . tape 31 , no. 3 , 1966, pp. 434-454 , doi : 10.2307 / 2270459 , JSTOR : 2270459 .
• AH Lachlan, RI Soare: Not every finite lattice is embeddable in the recursively enumerable degrees . In: Advances in Math . tape 37 , 1980, pp. 78-82 , doi : 10.1016 / 0001-8708 (80) 90027-4 .
• André Nies, Richard A. Shore, Theodore A. Slaman: Interpretability and definability in the recursively enumerable degrees . In: Proc. London Math. Soc. (3) . tape 77 , no. 2 , 1998, ISSN  0024-6115 , p. 241-291 , doi : 10.1112 / S002461159800046X .
• Emil L. Post: Recursively enumerable sets of positive integers and their decision problems . In: Bulletin of the American Mathematical Society . tape 50 , no. 5 , 1944, ISSN  0002-9904 , pp. 284-316 , doi : 10.1090 / S0002-9904-1944-08111-1 .
• Gerald Sacks : The recursively enumerable degrees are dense . In: Ann. Of Math. (2) . tape 80 , no. 2 , 1964, p. 300-312 , doi : 10.2307 / 1970393 , JSTOR : 1970393 .
• Richard A. Shore, Theodore A. Slaman: Defining the Turing jump . In: Mathematical Research Letters . tape 6 , 1999, ISSN  1073-2780 , pp. 711-722 .
• Stephen G. Simpson: First-order theory of the degrees of recursive unsolvability . In: Annals of Mathematics. Second series . tape 105 , no. 1 , 1977, ISSN  0003-486X , pp. 121-139 , doi : 10.2307 / 1971028 , JSTOR : 1971028 .
• Thomason, SK: Sublattices of the recursively enumerable degrees . In: Z. Math. Logic Basics Math . tape 17 , 1971, p. 273-280 , doi : 10.1002 / malq.19710170131 .
• CEM Yates: A minimal pair of recursively enumerable degrees . In: J. Symbolic Logic . tape 31 , no. 2 , 1966, p. 159-168 , doi : 10.2307 / 2269807 , JSTOR : 2269807 .