Volume-of-Fluid method

The volume-of-fluid method (often abbreviated as the VOF method ) is a numerical fluid mechanics procedure for treating two-phase flows. It is one of the standard methods in this area and is used almost exclusively with finite volume discretization . The method was first introduced in 1976 by William Noh and Paul Woodward. The first publication in a journal was in 1981 by Hirt and Nichols.

Basic idea

Schematic representation of the phase assignment in a Cartesian grid

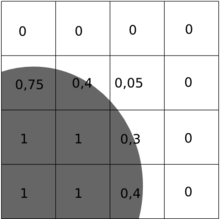
With the volume-of-fluid method, the volume fraction of a phase is saved as an additional variable within a calculation cell. This variable has the value 1 if only the first phase is within the calculation cell and the value 0 if only the second phase is in the cell. In cells with both phases, the value is between 0 and 1. The diagram on the right shows the assignment of the actual volume proportions (gray pitch circle) to the cells in a two-dimensional, Cartesian grid. The numerical values ​​are only to be understood symbolically and not exactly. The variable is calculated using the velocity field according to ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle \mathbf {u} }$

${\displaystyle {\frac {\partial C}{\partial t}}+\mathbf {u} \cdot \nabla C=0.}$

transported convectively . The physical properties such as density or viscosity are derived from the distribution of the phases. These values ​​are averaged in cells that contain both fluids. These values ​​are then used to calculate a new velocity field using the Navier-Stokes equations . With the volume-of-fluid method, the position of the interface between the fluids is only known implicitly. This has the advantage that topology changes, including decay and combination, of the free surface can be easily recorded, but the disadvantage that some boundary surface phenomena cannot be modeled. The volume-of-fluid method is conservative, which means that the volume of the phases is exactly retained when calculating the convective flows.

Method extensions

Geometric reconstruction

Schematic representation of the interface reconstruction with PLIC

Various supplements have been developed to improve the VOF method. Above all, this includes the geometric reconstruction of the interface, with which the accuracy of the flow calculation in interface cells can be significantly improved. The Piecewise Linear Interface Construction (PLIC) is the standard method in this area. The interface is approximated by a plane that is perpendicular to the normal vector in the cell. The position within the cell is selected in such a way that the volume proportions described by the variable result. Such a reconstruction is shown schematically in the adjacent picture. The red lines show the reconstructed interface. The polygon resulting from the cell walls and the interface is shifted by a distance formed from speed and time step length. The convective flows can then be determined from the intersection of the shifted polygon with the cell boundaries. ${\displaystyle \mathbf {n} }$ ${\displaystyle C}$

A detailed discussion can be found at Rider and Kothe.

Surface tension

In many phenomena with a free surface, surface tension plays a decisive role. That is why there are several models that allow the surface tension to be taken into account in VOF simulations. The two most important are: The Continuous Surface Force Method (CSF) according to Brackbill et al. a. and the Continuous Surface Stress Method (CSS) by Lafaurie et al. a.

Hybrid methods

Both the volume-of-fluid method and the related level-set method have different advantages and disadvantages. There have therefore been attempts to eliminate the disadvantages by combining both methods. The computational effort is significantly greater with hybrid methods than with the individual methods.

application areas

Example of a flow simulation using the VOF method

With the help of the Volume of Fluid method, many physical phenomena can be simulated with a free surface. This includes, for example, currents in partially filled containers. A typical application example is the dam breach scenario, which is often used as a validation for the numerical simulation of two-phase flows. The Volume of Fluid method can be combined with other models to simulate more complex phenomena. Together with heat transport, for example, heat-induced differences in density can be simulated. An example of this is the lava lamp.

Furthermore, phase transitions such as melting, solidification, evaporation and condensation can be simulated. Mixing processes can be represented with models for the material transport, chemical reactions in connection with two-phase flows are also possible. In addition, there are approaches with which non-Newtonian behavior can be simulated.

See also

• Direct numerical simulation
• Multiphase flow

Individual evidence

1. ^ WF Noh, P. Woodward: SLIC (Simple Line Interface Calculation) . In: Proceedings of the 5th International Conference of Fluid Dynamics . tape 59 , 1976, p. 330-340 .
2. ^ CW Hirt, BD Nichols: Volume of fluid (VOF) method for the dynamics of free boundaries . In: Journal of Computational Physics . tape 1 , no. 39 , 1981.
3. ^ WJ Rider, DB Kothe: Reconstructing volume tracking . In: Journal of Computational Physics . tape 141 , 1998, pp. 112-152 .
4. ↑ JU Brackbill, DB Kothe, C. Zemach: A continuum method for modeling surface tension. In: Journal of Computational Physics . No. 100 , 1992, pp. 335-354 .
5. ↑ B. Lafaurie, C. Nardone, R. Scardovelli, S. Zaleski, G. Zanetti: Modeling merging and fragmentation in multiphase flows with SURFER. In: Journal of Computational Physics . No. 113 , 1994, pp. 134-147 .
6. ↑ M. Sussman, EG Puckett: A Coupled Level Set and Volume-of-Fluid Method for Computing 3D and Axisymmetric Incompressible Two-Phase Flows. In: Journal of Computational Physics . No. 162 , 2000, pp. 301-337 .
7. ↑ youtube.com Simulation of a lava lamp
8. ↑ UD Kück, M. Kröger, M. Schlüter, N. Räbiger, D. Bothe, H.-J. Warnecke: Cross-scale transport processes in gas-liquid reactions . In: chemistry and engineering . tape 7 , no. 83 , 2011, p. 1084-1095 .