Direct numerical simulation

This article treats DNS as an abbreviation for Direct Numerical Simulation . For other meanings of DNS, see the DNS disambiguation .

Under Direct Numerical Simulation , short DNA , refers to a method of calculation of fluid mechanics for the mathematical solution of the full unsteady Navier-Stokes equations . It differs from other calculation methods in fluid mechanics in that small-scale turbulent fluctuations are numerically resolved in space and time and are not represented by turbulence models .

Due to the temporally varying, spatially small fluctuations in a turbulent flow , in addition to the high spatial resolution, an unsteady approach is required for the detailed description of the physical processes. The DNA is thus the most precise method of calculating currents; However, it also places the highest demands on the numerical method and the computing power available. That is why the DNA is mainly used in basic research. A large area of ​​application is the laminar - turbulent transition, by which one understands the transition from a smooth steady flow to the quasi- chaotic turbulent state. Furthermore, the DNS is used in the areas of detachment bubbles , fully turbulent flows and aeroacoustics and also serves to further develop turbulence models.

Underlying equations

Flow fields behave according to the Navier-Stokes equations . For low speeds with a Mach number less than 0.3 it is usually sufficient to use the Navier-Stokes equations for incompressible fluids. They essentially consist of three transport equations, the momentum equations in the three spatial directions. The conservation of mass results in incompressible flows that the speed is free from divergence . With increasing speed, compressibility effects play an increasingly important role, so that the Navier-Stokes equations for compressible fluids are to be applied. These are also necessary if, for example, aeroacoustic phenomena are to be investigated, since a finite speed of sound only results when the compressibility is taken into account . Since the Navier-Stokes equations for compressible flows are all transport equations, there are no elliptical terms in contrast to the equations for incompressible fluids . Depending on the application, additional equations can be included. For example, in hypersonic with a high Mach number, chemical reactions such as dissociation of molecules or ionization of atoms play a role.

Physical processes

Since the flow field in a DNS is to be calculated without a turbulence model, the flow-mechanical processes to be recorded by the method can be described most clearly using the laminar-turbulent transition. The term change, also called transition, is understood here to mean the transition from an originally laminar steady flow to a turbulent state, which is determined by small-scale, almost chaotic fluctuations. The reason for this is an instability of the flow with respect to small disturbances, which, depending on the respective flow state, exists from a certain Reynolds number . With the help of linear stability theory , the frequencies of the fanned disturbances and their fanning rates can be predicted very well for a given stationary flow field. For an incompressible plate boundary layer without a pressure gradient, z. B. fanned disturbances from a Reynolds number of Re⋅x ≈ 91,000, where x represents the coordinate in the direction of flow with its origin at the front edge of the plate. The local displacement thickness δ _{1 of} the boundary layer is often used instead of the downstream coordinate . This results in a critical Reynolds number of Reδ ₁ = 520, from which the first stimulated disturbances exist. These fanned disturbances, called Tollmien-Schlichting waves , grow exponentially in the downstream direction. If the instability waves reach a noticeable amplitude , they can no longer be viewed independently of one another, but interact with one another. In the Navier-Stokes equations, this results from the non-linear terms. If one subdivides a variable U into its stationary part u ₀ and the unsteady part u , this results from a non-linear term

${\displaystyle U\cdot U=(u_{0}+u)\cdot (u_{0}+u)=u_{0}^{2}+2\cdot u_{0}u+u^{2}}$

If one takes a wave of the form for the unsteady part

${\displaystyle u=u'\cdot e^{i(\alpha x)}}$

with the wave number α, the product of u with itself results

${\displaystyle U\cdot U=u_{0}^{2}+2u_{0}u'\cdot e^{i(\alpha x)}+u'^{2}\cdot e^{i(2\alpha x)}}$

that is, waves with twice the wave number are generated. The non-linear generation also causes an increase in disturbances that are actually linearly damped. Increasingly shorter-wave disturbances reach non-linear amplitudes and draw energy from the coarser scales. Since the second spatial derivative of a wave is proportional to the square of the wave number, the viscosity increasingly counteracts the generation for shorter-wave disturbances .

Depending on the disturbances introduced, different vortex structures result in the non-linear area. In the case of the boundary layer, a distinction is made between K-type (according to Philip Klebanoff ), H-type (according to Thorwald Herbert) and Oblique (English for crooked). In the later stages of the transition, the large eddy structures break open and a chaotic picture of small eddies results. Two-dimensional DNA is only useful in exceptional cases. In general, 2D turbulence does not exist. It is therefore generally necessary for a DNA to simulate the full three-dimensional Navier-Stokes equations, which means a correspondingly high computational effort.

Artificial streak image of the laminar-turbulent envelope in a plate boundary layer, calculated using DNA.

Comparison with other methods

One speaks of a DNS when all relevant scales are resolved spatially and temporally. This means that wave numbers have to be mapped cleanly until only the influence of viscosity counteracts the non-linear generation. Other methods of numerical fluid mechanics consider the unsteady processes of turbulence either to a limited extent or not at all. With the large eddy simulation (LES, in German also coarse structure simulation) one restricts oneself to the coarse turbulent scales by considering spatially filtered flow variables. The influence of the no longer resolved scales is represented by so-called subgridscale models. Since these models essentially introduce artificial viscosity , an under-resolved DNA can also be viewed as an LES.

On the other hand, RANS calculations (English for Reynolds-averaged Navier-Stokes equations) do not resolve any turbulent fluctuations, but instead completely model them using turbulence models. With the time-averaged Navier-Stokes equations, other equations than with DNS and LES are also solved, which is why a RANS result does not converge against the exact solution of the direct numerical simulation, even with any fine resolution.

Discretization procedure in the DNS

Sketch of an integration area for the DNA of a plate boundary layer.

The task of a numerical method for direct numerical simulation is therefore to resolve unsteady wave processes sufficiently finely in space and time. In addition, appropriate boundary conditions must be observed in order not to require an unnecessarily large calculation area and to avoid reflections at the edges. Typically, additional faults have to be introduced. In principle, disturbances are already inherent in the process (e.g. discretization errors, approximations in the initial and boundary conditions or rounding errors ), but the result then depends on the calculation grid used and, for rounding errors, even on the computer used. In addition, one would like to examine the influence of different disorders in a DNA.

Due to the high computational effort, DNS is usually limited to periodic boundary conditions in the third spatial direction. For the boundary layer on a flat plate, this means that an infinite extension in the transverse or spanwise direction is assumed. In the case of rotationally symmetrical bodies, the span direction then corresponds to the circumferential direction. The picture on the right shows an example of an integration area for the plate boundary layer .

Since the success of a DNA depends essentially on the ability to transport waves with sufficient accuracy, corresponding requirements must be placed on the numerics. Good dispersion and dissipation properties can be achieved in spatial discretization , which is why high-order methods are used almost exclusively. Due to the periodicity, a spectral approach is suitable for the span-wide direction, as this is ideal for wave transport. A spectral approach is possible in non-periodic spatial directions, but discretization methods that are not based on periodic boundary conditions are more practical. Examples of this are finite differences or finite volumes . Finite differences are often used in DNS codes because they are the fastest method for calculating high-order spatial derivatives on structured grids.

Due to the constant generation of higher harmonic waves, it is necessary for the stability of a calculation to remove short-wave interference. The problem with the short-wave components is that on a given grid only waves up to a certain wave number can be resolved. However, if waves are generated with wave numbers above this limit, these are mapped to a certain proportion on lower wave numbers (so-called aliasing), which generally leads to the process crashing. There is also an aliasing limit for the wave transport properties of every spatial discretization. For wave numbers above this aliasing limit, there is a negative group speed , i.e. these unsteady components run against the physically correct transport direction. From which wave number this occurs depends on the type and order of the procedure. With increasing order, the aliasing limit moves to higher wavenumbers. In principle, the short-wave components can also be removed through a correspondingly high spatial resolution. In this case, the viscosity ensures that these components are attenuated. However, this is not practical because it requires too great a spatial resolution. Common methods for dealiasing are spatial filtering with a low-pass filter , upwinding or alternating weighting of the discretization. In the case of a spectral discretization, the proportions are given as a function of the wave number. Dealiasing then takes place simply by setting high wavenumbers to zero (usually from 2/3 of the maximum wavenumber.)

The time derivative of the individual quantities results from the Navier-Stokes equations by means of space discretization. In principle, the time integration can be carried out with explicit or implicit methods. With an explicit time integration, the time step limit must be observed for a stable simulation . Depending on whether convective or viscous terms predominate, the time step scales proportionally or quadratically with the spatial resolution. The 4th order Runge-Kutta method is often used for time integration, as it has excellent properties in terms of accuracy and stability. Implicit methods have the advantage of not having a time step limit (at least in principle), but they require a significantly higher computational effort per time step. If one chooses the time step so roughly that an implicit compared to an explicit method is worthwhile, then the implicit integration dampens almost all instability waves away. For this reason, implicit integration methods are generally not used with DNS codes. An exception to this are compressible calculations with low Mach numbers , in which the time step of an explicit procedure must be very fine.

Due to the high computational effort, it is usually essential to compute on several processors. Since DNS codes typically work on structured grids and can therefore be vectorized well, a high computing power can be achieved on vector computers (e.g. Earth Simulator or NEC-SX8), which sometimes reaches over 50% of the theoretical computing power. Unstructured methods have so far not been able to establish themselves in DNS codes, since the greater flexibility with regard to the geometry is at the expense of the computing speed.

Initial and boundary conditions

Spatial and temporal simulations

As in linear stability theory, a distinction is made between temporal and spatial problems. In the case of a temporal simulation, disturbances that leave the integration area via the outflow edge are introduced again at the inflow edge. This means that disturbances increase in time to saturation . The background to this procedure is the fact that, from a mathematical point of view, due to the parabolic character of the viscous terms, boundary conditions must also be specified at the outflow edge. A periodic approach in the direction of flow avoids the problem of specifying the generally unknown suitable boundary conditions. A problem here is of course the fact that the flow at the outflow edge does not have the same state as at the inflow edge. For example, a boundary layer grows downstream or a pressure gradient in a channel ensures that the flow does not come to a standstill. The disturbance variables must therefore be scaled accordingly before they can be impressed on the inflow edge. Despite the problems and limitations of the temporal model, it is still used today, since a turbulent flow can be calculated with a relatively small integration area.

In a spatial simulation, however, the inflow and outflow edges are viewed separately from one another. This means that disturbances grow spatially (with the exception of the occurrence of absolute instability), which reflects reality much better. In a boundary layer, for example, Tollmien-Schlichting waves are transported downstream while they grow, which corresponds to an increase in amplitude in the downstream direction. After a sufficient simulation time, the disturbances reach a periodic state with periodic disturbance excitation. In a spatial simulation, it is particularly important to model a suitable outflow edge, since nonlinear interference would cause reflections on the outflow edge, which in turn leads to unphysical results. Initially, the integration area was lengthened over time in the downstream direction, so that disturbances could never reach the outflow edge running to the rear. However, this method becomes more and more complex as the simulation time increases. The breakthrough in spatial simulation came with the development of suitable damping zones in front of the outflow edge. Today the spatial model is mostly used.

Initial conditions

A solution of the boundary layer equations is typically used as the initial condition , since these represent a good approximation of a laminar flow subject to friction. With a plate boundary layer , self-similar profiles (Blasius or Falkner-Skan) can be interpolated onto the computational grid. If the geometries are more complex, the boundary layer equations must be integrated in the downstream direction. If this is not possible, e.g. B. due to backflow, the flow field can also be initialized with simple assumptions, since with clean boundary conditions initial disturbances should run out of the integration area.

boundary conditions

The boundary conditions for a wall can be formulated relatively easily. Due to the friction, the three speed components on the wall are zero ( stick condition ). In the compressible case, there is a further boundary condition for the temperature , which can be either isothermal or adiabatic. Isothermal means that the temperature is fixed, adiabatic that the heat flow and thus the normal wall temperature gradient is zero. Furthermore, actuators can be placed on the wall, e.g. B. an interference stripe for interference excitation to investigate the behavior of certain interference modes.

In the case of incompressible calculations and in supersonic conditions, all flow variables must be specified at the inflow edge. For compressible bills in subsonic z. B. to ensure by a characteristic boundary condition that upstream sound waves can leave the integration area. The inflow edge is also suitable for introducing defined disturbances. In the case of small disturbances, B. can be used to amplitude and phase curves from linear stability theory .

Boundary conditions that only arise due to the finite calculation grid are problematic. While RANS calculations typically only stipulate the steady-state free flow conditions, due to the unsteady solution, the choice of suitable boundary conditions is decisive for the success of a DNS. The outflow edge is of particular importance here, as reflections can significantly falsify the result due to the non-linear fluctuations. For this purpose, various damping zones have been developed in the past, in which z. B. the solution is drawn to a stationary basic flow. Particularly for aeroacoustic calculations, there are particularly strict requirements for the outflow edge, since the sound under consideration is orders of magnitude smaller than the fluidic fluctuations. One possibility here is the combination of grating and spatial low-pass filter , whereby unsteady components in the damping zone are successively removed from the solution before they cause reflections at the actual edge and contaminate the sensitive acoustic field.

Free flow edges are generally less critical than outflow edges, since the amplitudes that occur are significantly lower than at the outflow edge. However, unsuitable boundary conditions can lead to incorrect amplification rates of the interference waves or the correct solution requires an integration area that is too large. Due to the small fluctuations, the free flow margins are typically based on linearized formulations, such as B. Decay or characteristic boundary conditions. If periodicity in the transverse direction is assumed, the question of suitable boundary conditions does not arise at this point.

Scaling the problem with the Reynolds number

The scales to be resolved are determined by physics. The computational grid defines which scales can be resolved with a particular numerical method. The resulting required step size must therefore be in the order of magnitude (proportional to and not equal to) the smallest scales indicated by the Kolmogorov length scale

${\displaystyle \eta =(\nu ^{3}/\varepsilon )^{1/4}}$

can be determined, where the kinematic viscosity and ε is the dissipation rate of the kinetic energy. With a spatial step size h , the number of points is N in one spatial direction ${\displaystyle \nu }$

${\displaystyle N\sim {\frac {L}{h}}\sim {\frac {L}{\eta }}}$.

The dissipation rate ε of the kinetic energy can be estimated with the RMS value of the speed fluctuation u '

${\displaystyle \varepsilon \approx u'^{3}/L}$.

This results in the number of points required in one spatial direction

${\displaystyle N\sim {\frac {L}{\eta }}=\left({\frac {Lu'}{\nu }}\right)^{3/4}=\mathrm {Re} ^{3/4}}$

with the Reynolds number

${\displaystyle \mathrm {Re} ={\frac {u'L}{\nu }}}$.

If all three spatial directions are scaled with the Reynolds number, the total number of points required increases with Re ^9/4 . If one assumes periodic boundary conditions in the spanwise direction, then scaling the points in this direction with Re ^{3/4 is} not absolutely necessary, which means that the overall resolution only scales with Re ^3/2 . This can be further reduced, since z. B. the boundary layer thickness does not increase linearly with the downstream direction, which is why the number of points in the direction normal to the wall can scale less than with Re ^3/4 . The time to be simulated is proportional to the turbulent length scale τ represented by

${\displaystyle \tau ={\frac {L}{u'}}}$

given is. Assuming that the time step limit is dominated by convective terms (Δt ∼ h ∼ η / u '), the number of time steps results in

${\displaystyle N_{t}\sim {\frac {\tau }{\Delta {}t}}\sim {\frac {L}{\eta }}=\mathrm {Re} ^{3/4}}$

that is, the number of time steps to be calculated is scaled with the power ¾ of the Reynolds number. Thus, the total computational effort is proportional to Re ³ for a fully three-dimensional integration area without span-wide periodicity.

With a scaling factor for the overall problem of Re ^9/4 or Re ³ , application of the DNS to practical problems appears at first glance to be impossible. An evaluation of such large amounts of data (note that these are transient problems) does not appear to be practicable either. With DNS, however, it is not about simulating a complete aircraft, for example, rather one is interested in the physical fundamentals, through the understanding of which an overall system with high Reynolds numbers, such as the profile of a wing, can be improved. If, for example, methods are developed to maintain the laminar, it is sufficient to simulate the relevant area of ​​the boundary layer in order to reduce the drag of the entire aircraft.

evaluation of results

Instantaneous image of vortex structures in a shear layer . By introducing stationary span-wide disturbances, longitudinal vortices are generated which lead to the collapse of the Kelvin-Helmholtz vortices .

Since transient data from large areas are obtained from the DNS (around 100 million grid points for spatial resolution are quite common), huge amounts of data of several gigabytes are generated . Of course, statements about the physical processes cannot be derived directly from this; the data must be evaluated (postprocessing). Since in the spatial model the time course is periodic or at least quasi-periodic after sufficiently calculated time steps, it is advisable to examine the data by means of Fourier analysis . With periodic boundary conditions in the span direction, a double-spectral analysis is often carried out. The resulting modes are denoted by (h, k), where h is a multiple of the fundamental frequency and k is a multiple of the fundamental wavenumber

${\displaystyle \gamma ={\frac {2\pi }{\lambda _{z}}}}$

which results from the span λ _{z of} the integration area. The modes (0,1), (0,2) etc. denote stationary disturbances which are modeled over the third spatial direction. Correspondingly, a two-dimensional perturbation with the fundamental frequency is denoted by (1,0) and its higher harmonics by (2,0), (3,0) etc. The growth of the amplitudes in the direction of flow and the amplitude or phase curve normal to this can also be compared with the results of the linear stability theory.

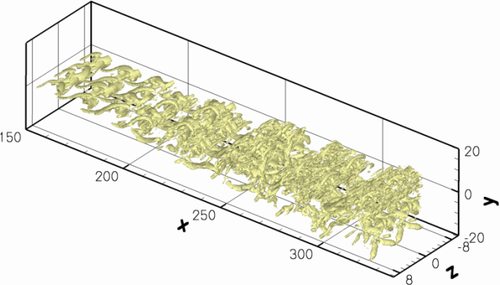
In the turbulent area, the amplitude curves are usually less meaningful because a large number of the modes have reached saturation . Therefore, vortices z. B. visualized with the help of the lambda2 criterion in order to get a better insight into the fluid mechanics. The picture shows an example of three-dimensional vortex structures in a shear layer using isosurfaces of the lambda2 criterion. By introducing stationary span-wide disturbances, longitudinal vortices are generated which lead to the collapse of the Kelvin-Helmholtz vortices. In order to show the sound radiation in aeroacoustic calculations, one can show the pressure itself, but also the dilation, the divergence of the velocity field. Density gradients give a nice impression because they can be used to create streak images. An evaluation program is z. B. EAS3 , which is used at various universities to evaluate DNS data.

History of DNA

The computation of a circular cylinder with Re = 10 from 1933 represents the beginning of numerical fluid mechanics . Thom achieved the solution by hand calculation using a difference method, which was already surprisingly accurate. The simulation by Orszag & Patterson from 1972, who calculated isentropic turbulence at Re = 35 on a 32 ³ grid using spectral methods, can be referred to as a first DNA in the true sense of the word . The first spatial DNA comes from Fasel in 1976. In this, the growth of small perturbations in a boundary layer was examined and compared with the linear stability theory. The turbulent flow in a flat channel with Re = 3300 and periodic boundary conditions in the direction of flow was described by Kim et al. calculated in 1987 on a grid with already 4 million points. In 1988 Spalart published DNS results for a turbulent boundary layer with Reθ = 1410 (θ stands for the momentum loss thickness of the boundary layer), which are also based on the time model. A breakthrough in the application of the spatial model came in the early 1990s with the development of suitable damping zones in front of the outflow edge, e.g. B. by Kloker et al. With the help of appropriate boundary conditions, Colonius et al. 1997 perform one of the first acoustic DNS, whereby the emitted sound of the simulated free shear layer was calculated directly by means of the Navier-Stokes equations and not according to an acoustic analogy. The largest DNA to date in terms of spatial resolution is a calculation by Kaneda and Ishihara from 2002, which was carried out on the Earth Simulator in Japan. They used 4096 ³ ≈ 68.7 billion grid points to simulate isentropic turbulence in a periodic integration area. The great progress that has been made in the area of ​​DNS is of course based on the one hand on the steadily increasing computer capacities, but also on the numerical processes that have been developed , which enable these resources to be used effectively.

application areas

Boundary layer separation on a profile.

An example for the application is the separation of a boundary layer due to a pressure gradient counteracting the flow. By stimulating the boundary layer with certain disturbances, an attempt is made to reduce the size of detachment bubbles or to avoid them entirely. Application examples are turbine blades or the wings on aircraft. If one were able to avoid stalling at a high angle of attack , higher lift coefficients could be achieved and one could do without landing flaps .

Another topic is laminar maintenance, which attempts to keep the boundary layer laminar beyond the natural range and to delay the transition from laminar to turbulent. This happens e.g. B. with suction or the introduction of longitudinal eddies in the boundary layer. Since a laminar boundary layer has a lower resistance than a turbulent one, this could reduce the kerosene consumption of aircraft by up to 15%.

In aeroacoustics , the mechanisms of sound generation caused by flow mechanical processes are investigated. The aim is to use appropriate actuators to reduce the emitted sound. Aeroacoustics is a relatively new field in the field of DNA, as it is relatively difficult to solve as a multi-scale problem. The fluid mechanical fluctuations, e.g. B. in a free shear layer, have large amplitudes with a small spatial extent. The emitted sound, on the other hand, is relatively long-wave with an extremely low amplitude. This means that special requirements ( boundary conditions , accuracy) have to be placed on a numerical method in order not to e.g. B. to falsify by reflections. An important aspect is jet noise , as it is one of the main sources of noise in an aircraft - especially during take-off. A breakthrough in this area would improve the quality of life for many airport residents. Due to requirements such. B. ban on night flights or noise-related takeoff / landing fees are also airlines and airport operators to a reduction of aircraft noise interested.

In the area of supersonic and hypersonic , it is necessary to map not only temporally averaged quantities, but also transient processes in the boundary layer, since high thermal loads can destroy the structure. The DNA is used for basic studies of the laminar-turbulent transition or for the development of cooling concepts. In order to take into account effects in hypersonic, more complex equations are now used that take into account chemical reactions such as dissociation or ionization , as well as thermal non-equilibrium.

DNA is also an important tool for modeling. The high-resolution unsteady flow data are used for the further development of turbulence models in order to improve less computationally intensive processes such as large eddy simulation or RANS calculations. It can also be used to validate the results of new fluid mechanics methods.

See also

• Large eddy simulation
• Reynolds averaged Navier-Stokes equations

literature

• Parviz Moin , Krishnan Mahesh: Direct Numerical Simulation. A Tool in Turbulence Research. In: Annual Review of Fluid Mechanics. Vol. 30, 1998, pp. 539-578, doi: 10.1146 / annurev.fluid.30.1.539 .
• Siegfried Wagner, Markus Kloker, Ulrich Rist: Recent Results in Laminar-Turbulent Transition . Springer Verlag, Berlin et al. 2003, ISBN 3-540-40490-2 ( series of publications: Notes on numerical fluid mechanics and multidisciplinary design 86).
• Peter J. Schmid, Dan S. Henningson: Stability and Transition in Shear Flows . Springer Verlag, Berlin et al. 2001, ISBN 0-387-98985-4 ( Applied Mathematical Sciences 142).
• Hermann Schlichting , Klaus Gersten : boundary layer theory . 9th completely revised and expanded edition. Springer Verlag, Berlin et al. 1997, ISBN 3-540-55744-X .
• John D. Anderson : Computational Fluid Dynamics. The basics with applications . McGraw-Hill, New York et al. 1995, ISBN 0-07-113210-4 ( McGraw-Hill series in aeronautical and aerospace engineering ).

Individual evidence

1. ↑ Direct numerical simulation & rough structure simulation of turbulent flows. Retrieved July 1, 2019 . 
2. ↑ P. Klebanoff, K. Tidstrom: Evolution of Amplified Waves Leading to transition in a boundary layer with Zero Pressure Gradient. NASA TN D-195, 1959.
3. ^ T. Herbert: Secondary Instability of Boundary Layers. Annual Review of Fluid Mechanics , Vol. 20, 1988, pp. 487-526, doi: 10.1146 / annurev.fl.20.010188.002415
4. ↑ ^{a b} S. Lele: Compact finite differences with spectral-like resolution. Journal of Computational Physics, Vol. 103, 1992, pp. 16-42, ISSN  0021-9991
5. ↑ M. Kloker: A robust high-resolution split-type compact FD scheme for spatial DNS of boundary-layer transition. Applied Scientific Research, Vol. 59, 1998, pp. 353-377, doi: 10.1023 / A: 1001122829539
6. ↑ C. Canuto, M. Hussaini, A. Quarteroni: Spectral Methods in Fluid Dynamics. In: Springer series in computational physics , Springer Verlag, New-York 1988, ISBN 0-387-17371-4 .
7. ↑ ^{a b c} M. Kloker, U. Konzelmann, H. Fasel: Outflow boundary conditions for spatial Navier-Stokes simulations of transition boundary layers. AIAA Journal, Vol. 31, No 4, 1993, pp. 355-383, ISSN  0001-1452
8. ↑ ^{a b} T. Colonius, S. Lele, P. Moin: Sound generation in a mixing layer. Journal of Fluid Mechanics, Vol. 330, 1997, pp. 375-409, ISSN  0022-1120
9. ↑ A. Babucke, M. Kloker, U. Rist: DNA of a Plane Mixing Layer for the Investigation of Sound Generation Mechanisms. Computers and Fluids, Vol. 37, Issue 4, 2008, pp. 360-368, doi: 10.1016 / j.compfluid.2007.02.002
10. ^ J. Jeong, F. Hussain: On the identification of a vortex. Journal of Fluid Mechanics, Vol. 285, 1995, pp. 69-94, doi: 10.1017 / S0022112095000462
11. ↑ A. Thom: The flow past a circular cylinder at low speeds. Proceedings of the Royal Society of London. Series A, Vol. 141, 1933, p. 651.
12. ^ S. Orszag, G. Patterson: Numerical simulation of three-dimensional homogeneous isotropic turbulence. Physical Review Letters, Vol. 28, 1972, pp. 76-79, doi: 10.1103 / PhysRevLett.28.76
13. ^ H. Fasel: Investigation of the stability of boundary layers by a finite-difference model of the Navier-Stokes equations. Journal of Fluid Mechanics, Vol. 78, No 2, 1976, pp. 620-628, doi: 10.1017 / S0022112076002486
14. ^ J. Kim, P. Moin, R. Moser: Turbulence statistics in fully-developed channel flow at low Reynolds number. Journal of Fluid Mechanics, Vol. 177, 1987, pp. 133-66, doi: 10.1017 / S0022112087000892
15. ↑ P. Spalart: Direct numerical simulation of a turbulent boundary layer up to Rθ = 1410. Journal of Fluid Mechanics, Vol. 187, 1988, pp. 61-98, doi: 10.1017 / S0022112088000345
16. ^ Y. Kaneda, T. Ishihara: High-resolution direct numerical simulation of turbulence. Journal of Turbulence, Vol. 7, No. 20, 2006.
17. ↑ Cheaper flying - with perforated wings , article on Spiegel Online , 2006.
18. ^ C. Stemmer, N. Mansour: DNS of transition in hypersonic boundary-layer flows including high-temperature gas effects. Center for Turbulence Research, Annual Research Briefs, 2001, pdf ( Memento from July 9, 2010 in the Internet Archive )

Web links

Commons : Direct Numerical Simulation  - collection of images, videos and audio files

• Gallery with DNS results at the Center of Turbulence Research ( Memento from May 18, 2013 in the Internet Archive )
• Animation of the vortex structures during boundary layer change (K-type)

This version was added to the list of articles worth reading on December 6, 2007 .