Linear stability theory

This article deals with the growth of small perturbations in a flow field. For further meanings of the term linear stability theory see Stability Theory .

The linear stability theory (LST for short) describes physically in a flow the growth of undulating disturbances with small amplitudes . By specifying a stationary flow field, the rate of expansion and the shape of the linear disturbances can be determined as a function of frequency or wave number . This explains well why some currents do not reach a steady state. Despite the local approach, it can be used to describe the initial area of ​​the laminar-turbulent transition. The e ^N method, which is a common method for estimating the position of the laminar-turbulent transition, is based on the amplification rates from the linear stability theory.

history

Many currents that occur in nature and technology are turbulent . A laminar flow results only with a small Reynolds number . For a long time it was unclear why a laminar flow changes and a turbulent state occurs downstream. One of the first hypotheses was that the laminar flow is unstable. Starting in the 1880s, John William Strutt, 3rd Baron Rayleigh , published various results on the instability of frictionless flows and discovered that a flow field becomes unstable when a turning point occurs in the velocity profile. Although this could already explain the unsteady behavior of a free jet , the question of why a boundary layer becomes turbulent remained open. As early as 1915, Geoffrey Ingram Taylor suspected that friction could also have a destabilizing effect. Typically, however, a stabilizing influence of the viscous terms was assumed, so that in 1921 Fritz Noether assessed the approach of small disturbances as unsuccessful on the basis of previous research results. Remarkably, in the same year Ludwig Prandtl made similar assumptions as Taylor did and initiated research on friction-related stability theory in Göttingen . Werner Heisenberg dealt with the laminar-turbulent transition as part of his dissertation, but it was Walter Tollmien who succeeded in developing the friction- related stability theory. One of the first applications of the linear stability theory was in 1933 by Hermann Schlichting . Before the beginning of the computer age, Pretsch carried out the first systematic stability calculations for boundary layers of the Falkner-Skan family in 1942.

Outside of Germany , the linear stability theory received little attention at first because the predicted instability waves could not be measured. In addition, skepticism prevailed that a linear approach should allow meaningful statements for a highly non-linear phenomenon such as turbulence. The Göttingen approach was only confirmed by the experimental proof of instability waves in a plate boundary layer by Schubauer and Skramstadt in the early 1940s ( the results were published in 1947 due to the war-related censorship). Smith and Gamberoni as well as Van Ingen developed the e ^N method from linear stability theory , which is still used today for transition prediction. With the beginning of the computer age in the 1960s, the stability properties of numerous boundary layer configurations were calculated. In 1982 Mack was able to demonstrate additional instability modes in supersonic boundary layers by means of the linear stability theory, which are also called Mack modes in his honor.

Basics of the linear stability theory

The linear stability theory considers the stability of a flow against small disturbances. It is assumed here that the flow field is constant in the transverse direction. For the boundary layer, this means that on a flat plate with the direction of flow and the direction normal to the wall, the basic flow is constant over the spanwise direction, which corresponds to an infinite expansion in the direction. In order to be able to mathematically record the behavior of small disturbances, the flow variables in the Navier-Stokes equations are subdivided into a specified stationary basic flow and unsteady disturbance variables. For the three speed components in -, - and - direction as well as density , pressure and temperature we get: ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle u,v,w}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle z}$ ${\displaystyle \rho }$ ${\displaystyle p}$ ${\displaystyle T}$

${\displaystyle u=U_{0}(x,y)+u'(x,y,z,t),\quad v=V_{0}(x,y)+v'(x,y,z,t),\quad w=W_{0}(x,y)+w'(x,y,z,t)}$

${\displaystyle \rho =\rho _{0}(x,y)+\rho '(x,y,z,t),\quad p=P_{0}(x,y)+p'(x,y,z,t),\quad T=T_{0}(x,y)+T'(x,y,z,t)}$

Assumptions

Based on this, the following assumptions are made:

1. The stationary basic flow fulfills the Navier-Stokes equations. As a result, all terms in the Navier-Stokes equations that do not contain any disturbance variables disappear.
2. Parallel basic flow. It is z. B. neglecting the thickening of a boundary layer. It follows from the continuity equation that the normal velocity component V _{0 is} neglected for the basic flow . This results in a local theory in which each position x in the downstream direction is considered separately. It follows: ${\displaystyle U_{0}=U_{0}(y),\quad W_{0}=W_{0}(y),\quad P_{0}=P_{0}(y),\dots \quad V_{0}=0}$
3. Small glitches. Assuming small disturbances, the equations can be linearized with respect to the basic flow. With this all squares of the disturbance variables disappear from the equations.

Fault approach

A wave approach is used for the disturbance variables. B. for , the disturbance speed in -direction, has the following form: ${\displaystyle u'}$ ${\displaystyle x}$

${\displaystyle u'={\hat {u}}(y)\cdot e^{i(\alpha x+\gamma z-\omega t)}}$

This corresponds to a wave with the wave numbers and in - or - direction with the frequency , the amplitude and phase curves of which are a function of . The individual quantities are generally complex and have the following physical meaning: ${\displaystyle \alpha _{r}}$ ${\displaystyle \gamma }$ ${\displaystyle x}$ ${\displaystyle z}$ ${\displaystyle \omega _{r}}$ ${\displaystyle y}$

• ${\displaystyle \alpha _{r}}$= Wave number in flow direction (wave length ) ${\displaystyle \lambda _{x}=2\pi /\alpha _{r}}$
• ${\displaystyle \gamma }$= Wave number in transverse direction (wave length ) ${\displaystyle \lambda _{z}=2\pi /\gamma }$
• ${\displaystyle k={\sqrt {\alpha _{r}^{2}+\gamma _{r}^{2}}}}$ = Wave number in the direction of propagation
• ${\displaystyle \omega _{r}}$= Angular frequency (period duration ) ${\displaystyle \lambda _{T}=2\pi /\omega _{r}}$
• ${\displaystyle \alpha _{i}}$= spatial expansion rate in the direction (expansion for <0) ${\displaystyle x}$ ${\displaystyle \alpha _{i}}$
• ${\displaystyle \omega _{i}}$= temporal increase rate (increase for > 0) ${\displaystyle \omega _{i}}$
• ${\displaystyle \left|{\hat {u}}(y)\right|}$= Amplitude curve from over ${\displaystyle u'}$ ${\displaystyle y}$
• ${\displaystyle \arg\{{\hat {u}}(y)\}}$= Phase progression from over ${\displaystyle u'}$ ${\displaystyle y}$
• ${\displaystyle \omega _{r}/\alpha _{r}}$= Phase velocity of the interfering wave in -direction ${\displaystyle x}$
• ${\displaystyle \partial \omega _{r}/\partial \alpha _{r}}$= Group speed of the interfering wave in the direction ${\displaystyle x}$

The span-wide wave number is a real quantity due to the infinite expansion of the flow in the -direction, since an imaginary part would correspond to a spatial growth in the span-wide direction. ${\displaystyle \gamma }$ ${\displaystyle z}$ ${\displaystyle \gamma _{i}}$

Temporal and spatial model

In the linear stability theory, a distinction is made between temporal and spatial models. In the case of the time model, the real wave numbers and are specified, from which the frequency and the temporal increase rate result. In the case of the spatial problem, by specifying the transverse wave number and the real frequency, one receives the wave number in the direction and the spatial amplification rate . ${\displaystyle \alpha _{r}}$ ${\displaystyle \gamma }$ ${\displaystyle \omega _{r}}$ ${\displaystyle \omega _{i}}$ ${\displaystyle \gamma }$ ${\displaystyle \omega _{r}}$ ${\displaystyle x}$ ${\displaystyle \alpha _{r}}$ ${\displaystyle \alpha _{i}}$

Whether the temporal or the spatial problem is to be applied depends on the respective problem: if it is a convective instability, the spatial problem is to be selected, in the case of an absolute instability the temporal one. In many cases, the spatial approach is more realistic, since z. B. in a boundary layer, the disturbances are convected downstream during the growth, which corresponds to a growth in space.

Guest transformation

The Gaster transformation enables the transformation between temporal and spatial models for almost neutral waves, that is, assuming small amplification rates:

${\displaystyle {\frac {\omega _{i}^{\mathrm {zeit} }}{\alpha _{i}^{\mathrm {raum} }}}=-{\frac {\partial \omega _{r}}{\partial \alpha _{r}}}}$

where it is assumed that the frequency and wave number do not differ significantly in the spatial and temporal model: ${\displaystyle x}$

${\displaystyle \alpha _{r}^{\mathrm {raum} }\approx \alpha _{r}^{\mathrm {zeit} },\quad \omega _{r}^{\mathrm {raum} }=\omega _{r}^{\mathrm {zeit} }}$

Incompressible stability equations

Due to the elliptical form of the continuity equation for incompressible flows, neglecting compressibility effects results in the Orr-Sommerfeld and Squire equation for describing the linear stability. Together these form a sixth order system of equations.

Orr-Sommerfeld equation

For incompressible flows, the linear stability problem is described by the Orr-Sommerfeld equation (after William McFadden Orr 1907, Arnold Sommerfeld 1908):

${\displaystyle {\begin{aligned}0=&\left(\alpha u_{0}+\gamma w_{0}-\omega \right)\left({\hat {v}}_{yy}-\left(\alpha ^{2}+\gamma ^{2}\right){\hat {v}}\right)\,-\,\left(\alpha u_{0yy}+\gamma w_{0yy}\right){\hat {v}}\\&{}+{\frac {i}{Re}}\left({\hat {v}}_{yyyy}-2\left(\alpha ^{2}+\gamma ^{2}\right){\hat {v}}_{yy}+\left(\alpha ^{2}+\gamma ^{2}\right)^{2}{\hat {v}}\right)\end{aligned}}}$

The Orr-Sommerfeld equation is an ordinary fourth order differential equation with the complex amplitude function as the only variable. The equation can also be understood as an eigenvalue problem with the eigenvalue and the eigenvector . Since there are up to fourth derivatives of the quantity to be solved, four boundary conditions are required. ${\displaystyle {\hat {v}}}$ ${\displaystyle \omega }$ ${\displaystyle {\hat {v}}(y)}$

• If the edge is a wall, the stick condition and the continuity equation result in:

${\displaystyle {\hat {v}}(y_{\mathrm {Wand} })=0,\quad {\hat {v}}_{y}(y_{\mathrm {Wand} })=0}$

• In the case of a free flow edge, the complex amplitude function must decay towards the far field. It can be shown that the decay rate in the -direction corresponds to the wave number in the downstream direction. ${\displaystyle y}$

${\displaystyle {\hat {v}}(y=\infty )=0,\quad {\hat {v}}_{y}(y=\infty )=0}$

Squire equation

The solution of the Orr-Sommerfeld equation provides amplitude and phase curves for the disturbance of the normal velocity component . For a purely two-dimensional case ( , ), the curves of the other speed components can be calculated from the continuity equation. In the general three-dimensional case, however, the Squire equation is required to calculate the cross-flow components: ${\displaystyle v}$ ${\displaystyle W_{0}=0}$ ${\displaystyle \gamma =0}$ ${\displaystyle u}$

${\displaystyle i\left(\alpha u_{0}+\gamma w_{0}-\omega \right){\hat {\Omega }}-{\frac {1}{Re}}\left({\hat {\Omega }}_{yy}-\left(\alpha ^{2}+\gamma ^{2}\right){\hat {\Omega }}\right)=i\left(\alpha w_{0y}-\gamma u_{0y}\right){\hat {v}}}$

with the (wall) normal vortex strength

${\displaystyle {\hat {\Omega }}=i(\gamma {\hat {u}}-\alpha {\hat {w}})}$

as the variable to be solved from which the disturbance variables of the speed components and can be calculated. The curve from the Orr-Sommerfeld equation on the right-hand side is to be used here. The homogeneous solutions of the Squire equation (with ) are also valid and physically meaningful solutions and are called Squire modes. Squire proved that these fashions are always subdued. ${\displaystyle u}$ ${\displaystyle w}$ ${\displaystyle {\hat {v}}}$ ${\displaystyle {\hat {v}}=0}$

Compressible stability equations

If the compressibility is taken into account, the continuity equation cannot eliminate a variable from the equations, as was the case with the incompressible approach. With the above-mentioned assumptions and the disturbance approach, an eighth order system of equations results, which consists of five equations. According to the order of the system of equations, a total of eight boundary conditions must be met:

• As in the incompressible case, the sticking condition applies to the wall boundary condition. Assuming that the wall is thermally inert and temperature fluctuations with frequencies of up to many kilohertz, as they are e.g. B. occur in supersonic boundary layers, the disturbance variable of the temperature on the wall is also set to zero.

${\displaystyle {\hat {u}}(y_{\mathrm {Wand} })=0,\quad {\hat {v}}(y_{\mathrm {Wand} })=0,\quad {\hat {w}}(y_{\mathrm {Wand} })=0,\quad {\hat {T}}(y_{\mathrm {Wand} })=0}$

• Similar to the incompressible case, it applies at the free flow edge that the disturbances must subside towards the outside. However, a direct correlation between the decay rate and wave number cannot be established. If the free flow edge is far enough away, the disturbance variables can also be set directly to zero as a good approximation.

Findings from linear stability theory

From the linear stability theory, essential physical knowledge about the stability of flows and thus about the cause of the laminar-turbulent change can be derived.

Friction-free instability

For frictionless flows ( ) the following theorems can be derived from the linear stability theory: ${\displaystyle Re\rightarrow \infty }$

• Rayleigh Theorem No. 1:

A necessary condition for frictionless instability is a turning point in the speed profile.

• Rayleigh Theorem No. 2:

The phase velocity of a fanned disturbance is always between the minimum and the maximum value of the basic flow u (y).

• Tollmien theorem:

For a boundary layer it is necessary and sufficient for frictionless instability that the basic flow has a turning point.

A turning point thus has a significant influence on the stability behavior. It also follows from Tollmien's theorem that the Blasius boundary layer only becomes unstable through the influence of friction.

Boundary layer instabilities

Stability diagram for the Blasius boundary layer.

If you carry out a stability analysis for different frequencies at several positions in the downstream direction, you get a stability diagram. Such a stability diagram for two-dimensional waves ( ) is shown on the right for the incompressible Blasius boundary layer . The range of amplification is given as a function of the frequency and the Reynolds number, formed with the local displacement thickness. The neutral curve (blue here) indicates the area in which disturbances are dampened or fanned. It can be seen that from a Reynolds number , the critical Reynolds number, an amplification of disturbances exists for the first time. Further downstream, the area of ​​amplification shifts to lower frequencies. Due to the shape of the neutral curve in the stability diagram, the term stability banana is often used. ${\displaystyle \gamma =0}$ ${\displaystyle \omega }$ ${\displaystyle \delta _{1}}$ ${\displaystyle Re_{\delta _{1}}=520}$

Spectrum of the Blasius boundary layer.

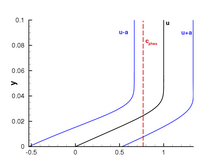
The time spectrum for the Blasius boundary layer at this point is shown in the figure on the right for a wave number . There is a single fanned eigenvalue ( ) at a frequency that corresponds to the Tollmien-Schlichting wave (TS wave for short). To the right of the fanned eigenvalue is the continuous spectrum, the disturbances of which are all attenuated. The continuous spectrum corresponds to disturbances in the potential flow, accordingly its phase velocity is equal to the dimensionless free flow velocity ( ). The damped squire modes, which result from the homogeneous solution of the squire equation ( ) and thus only have perturbations in and , are below the amplified eigenvalue . ${\displaystyle Re_{\delta _{1}}=1000}$ ${\displaystyle \alpha _{r}=0{,}3}$ ${\displaystyle \omega _{i}}$ ${\displaystyle \omega _{r}=0{,}135}$ ${\displaystyle U_{\infty }=1}$ ${\displaystyle {\hat {v}}=0}$ ${\displaystyle u}$ ${\displaystyle w}$

Eigenfunction of the fanned eigenvalue: U-profile of the Tollmien-Schlichting wave.

The eigenfunction belonging to the fanned eigenvalue shows the typical course of a TS wave for the amplitude of the velocity component with the global maximum within the boundary layer and a further local maximum at the boundary layer edge. Outwardly, the disturbance subsides exponentially. There is a phase jump around the zero crossing of the amplitude . ${\displaystyle u}$ ${\displaystyle \pi }$

Influence of the slip angle

The slip angle indicates the angle between the direction of propagation of the disturbance wave and the longitudinal direction of flow. The following applies to the influence of the slip angle on the inflation rates in an incompressible flow: ${\displaystyle \psi =\operatorname {atan} (\gamma /\alpha _{r})}$

• Squire theorem:

The smallest critical Reynolds number for two-dimensional interference waves results for an incompressible two-dimensional basic flow.

The derivation of the Squire theorem from the Orr-Sommerfeld equation can be found e.g. B. in.

Influence of the pressure gradient

From the linear stability theory it follows that a negative pressure gradient stabilizes the flow, whereas a pressure increase in the flow direction has a destabilizing effect. The reason for this lies in the shape of the speed profiles: A negative pressure gradient causes a fuller speed profile, whereas a strong positive pressure gradient causes a turning point in the u-profile. ${\displaystyle \partial p/\partial x<0}$

Supersonic boundary layers

Sketch of the local supersonic area of ​​the phase velocity.

With increasing flow velocity, compressibility effects play an increasingly important role. From a Mach number of Ma = 3, there is a local supersonic area on the wall for the phase velocity that is constant above the direction normal to the wall, in which the phase velocity is greater than the sum of the local flow and sound velocity. This causes an additional instability to occur, commonly referred to as the second mode. A zero point in the eigenfunction of the pressure is characteristic of the second mode. The thickness of the local supersonic area of ​​the phase velocity is a measure for the amplification of the second mode.

An increase in the Mach number usually results in a smaller, more critical Reynolds number, the minimum value of which is reached at a Mach number of approximately 4.5. From a Mach number of 5, the instability areas of the first and second modes are combined in the stability diagram.

The compressibility also has an influence on the propagation angle of the maximally fanned disturbance. While in the incompressible case for a two-dimensional boundary layer the most fanned disturbance has a skew angle of zero degrees, it increases at supersonic from approx. 40 ° at Mach 1 to its maximum value of 65 ° at Mach 3.

The stability behavior of the boundary layer can be strongly influenced by the wall temperature: it is possible to stabilize the first mode by cooling, but this leads to higher amplification rates in the second mode.

Numerical solution methods

There are two numerical methods for solving the linear stability equations, the matrix method and the shooting method. Since the basic flow profiles are specified, the occurring y-derivatives of the basic flow can be regarded as known with both methods, since they are e.g. B. can be calculated with finite differences.

Matrix method

In the matrix method, often referred to as the direct method, the stability equations to be solved are represented in matrix form. The individual terms are sorted according to the derivatives of the quantities to be solved. This results in an eigenvalue problem with the eigenvalue . The eigenvectors consist of the values ​​of the complex amplitude functions at the discrete positions. Since the viscous terms of the Navier-Stokes equations also contain second derivatives, terms also appear in linear stability theory . Thus the eigenvalue problem only exists for the temporal model; with the spatial approach a quadratic eigenvalue problem would have to be solved. ${\displaystyle y}$ ${\displaystyle \omega }$ ${\displaystyle y}$ ${\displaystyle x}$ ${\displaystyle \alpha ^{2}}$

In the two-dimensional Orr-Sommerfeld equation, the terms are sorted according to the derivatives of and the occurrence of the eigenvalue : ${\displaystyle y}$ ${\displaystyle {\hat {v}}}$ ${\displaystyle \omega }$

${\displaystyle \left[-\alpha ^{3}U_{0}-\alpha U_{0yy}+{\frac {i\alpha ^{4}}{Re}}\right]\cdot {\overline {v}}+\left[\alpha U_{0}-{\frac {i\cdot 2\alpha ^{2}}{Re}}\right]\cdot {\overline {v}}_{yy}+\left[{\frac {i}{Re}}\right]\cdot {\overline {v}}_{yyyy}=\omega \left[1\right]\cdot {\overline {v}}_{yy}+\omega \left[-\alpha ^{2}\right]\cdot {\overline {v}}}$

Here stands for the complex eigenvector that is derived from the values ​​of ${\displaystyle {\overline {v}}}$

${\displaystyle {\hat {v}}(y)}$at the discrete points. ${\displaystyle y}$

The derivatives of can be determined using finite differences. Thus the derivative of is a linear combination of the individual discrete values, which is why the derivatives can be expressed by a matrix operation: ${\displaystyle y}$ ${\displaystyle {\overline {v}}}$ ${\displaystyle y}$ ${\displaystyle {\overline {v}}}$ ${\displaystyle y}$

${\displaystyle {\overline {v}}_{yy}={\overline {D}}_{2}\cdot {\overline {v}}}$

${\displaystyle {\overline {v}}_{yyyy}={\overline {D}}_{4}\cdot {\overline {v}}}$

The derivation matrices contain the coefficients of the corresponding finite differences. This allows the matrix notation of the Orr-Sommerfeld equation to be set up:

${\displaystyle {\overline {A}}_{0}\cdot {\overline {v}}+{\overline {A}}_{2}\cdot {\overline {v}}_{yy}+{\overline {A}}_{4}\cdot {\overline {v}}_{yyyy}=\omega \left({\overline {B}}_{0}\cdot {\overline {v}}+{\overline {B}}_{2}\cdot {\overline {v}}_{yy}\right)}$

${\displaystyle \left[{\overline {A}}_{0}+{\overline {A}}_{2}\cdot {\overline {D}}_{2}+{\overline {A}}_{4}\cdot {\overline {D}}_{4}\right]\cdot {\overline {v}}=\omega \left[{\overline {B}}_{0}+{\overline {B}}_{2}\cdot {\overline {D}}_{2}\right]\cdot {\overline {v}}}$

${\displaystyle {\overline {A}}\cdot {\overline {v}}=\omega \cdot {\overline {B}}\cdot {\overline {v}}}$

In matrices , , which are only main diagonal with the corresponding terms of the occupied Orr-Sommerfeld equation. For example, the main diagonal of the matrix consists of the elements , where j is the y index. The eigenvalue problem of the resulting matrices and can then by means of numerical libraries, e.g. B. LAPACK can be solved. ${\displaystyle {\overline {A}}}$ ${\displaystyle {\overline {A}}_{2}}$ ${\displaystyle {\overline {A}}_{4}}$ ${\displaystyle {\overline {A}}_{2}}$ ${\displaystyle a_{2}(j,j)=\alpha \cdot U0(j)-i{\frac {2\alpha ^{2}}{Re}}}$ ${\displaystyle {\overline {A}}}$ ${\displaystyle {\overline {B}}}$

If one is interested in the spatial solution, there is the possibility of iterating the eigenvalue under consideration on the spatial problem. For this purpose, the imaginary part is iterated in such a way that the imaginary part of this eigenvalue becomes zero. The necessary determination of the eigenvalue of an only slightly modified matrix can e.g. B. be done with the Wielandt iteration . The actual iteration can then e.g. B. by means of the Newton method or similar methods. ${\displaystyle \alpha _{i}}$ ${\displaystyle \omega _{i}}$

The great advantage of the matrix method is that the entire spectrum can be obtained without specifying estimated values. However, it is relatively computationally intensive, especially when iterating on the spatial solution.

Shooting procedure

In the shooting method, the original boundary value problem is viewed as an initial value problem and the missing initial conditions are determined by iteration. For this purpose, the original differential equations are to be converted into a system of first-order differential equations. The following system of equations results as an example for the two-dimensional Orr-Sommerfeld equation:

${\displaystyle z_{0}={\hat {v}}}$

${\displaystyle {\frac {\partial z_{0}}{\partial y}}=z_{1}}$

${\displaystyle {\frac {\partial z_{1}}{\partial y}}=z_{2}}$

${\displaystyle {\frac {\partial z_{2}}{\partial y}}=z_{3}}$

${\displaystyle {\frac {\partial z_{3}}{\partial y}}=\left(-\omega \alpha ^{2}+\alpha ^{3}u_{0}+\alpha u_{0yy}-{\frac {i\alpha ^{4}}{Re}}\right)\cdot z_{0}+\left(\omega -\alpha u_{0}+{\frac {i2\alpha ^{2}}{Re}}\right)\cdot z_{2}}$

This system of equations is now to be integrated over the direction. For the free flow edge (parallel flow outside the boundary layer) the following fundamental solutions of the form can be derived: ${\displaystyle y}$ ${\displaystyle {\hat {v}}(y)\sim e^{\lambda \cdot y}}$

• friction-free fundamental solution:

${\displaystyle \lambda _{1,2}=\pm \alpha }$

• viscous fundamental solution:

${\displaystyle \lambda _{3,4}=\pm {\sqrt {\alpha ^{2}+i\cdot Re(\omega +\alpha u_{0})}}}$

Due to the subsiding of the disturbances to the outside, there is only one physically meaningful solution per fundamental solution. For the example of a boundary layer with the wall at, it follows that due to the condition ${\displaystyle y=0}$

${\displaystyle {\hat {v}}(y=\infty )={\hat {v}}_{y}(y=\infty )=0}$

only the negative fundamental solutions make physical sense. By choosing the integration direction starting from the far field towards the wall, it can be achieved that the unphysical solutions are dampened. ${\displaystyle \lambda _{2,4}<0}$ ${\displaystyle \lambda _{1,3}>0}$

The basic procedure for the spatial solution z. B. a boundary layer then looks such that the frequency and, in general three-dimensional case, the wavenumber over a wide range are specified. Starting from the free-flow edge, the two fundamental solutions are integrated for an estimated wave number along the directions. It is usually necessary to carry out an orthonormalization in order to suppress an increase in the other fundamental solution. ${\displaystyle \omega _{r}}$ ${\displaystyle \gamma }$ ${\displaystyle \lambda _{2,4}}$ ${\displaystyle \alpha }$ ${\displaystyle y}$

The linear combination of the two fundamental solutions and the wave number must then be iterated in such a way that the wall boundary conditions: are met. When integrating over the direction, the stability limit of the method used must of course be observed. ${\displaystyle \alpha }$ ${\displaystyle {\hat {v}}(y=0)={\hat {v}}_{y}(y=0)=0}$ ${\displaystyle y}$

The main advantage of the shooting method is its speed, since there are no large systems of equations to solve. It is equally suitable for the temporal and spatial problem. A disadvantage is the specification of meaningful estimated values, which can be a problem, especially for high Mach numbers. The procedure shown for the boundary layer can only be transferred to a limited extent to other flows such as a free shear layer .

literature

• H. Schlichting, K. Gersten: boundary layer theory . 9th edition. Springer Verlag, Berlin 1997, ISBN 3-540-55744-X .
• L. Mack: Boundary-layer linear stability theory. In: AGARD Special Course on Stability and Transition of Laminar Flow. AGARD R-709, 1984.
• B. Bayly, S. Orszag, T. Herbert: Instability mechanisms in shear-flow transition. In: Annual Review of Fluid Mechanics . , Vol. 20, pp. 359-391, 1988, doi : 10.1146 / annurev.fl.20.010188.002043
• P. Schmid, D. Henningson: Stability and Transition in Shear Flows . In: Applied Mathematical Sciences . tape 142 . Springer Verlag, Berlin 2001, ISBN 0-387-98985-4 .

Individual evidence

1. ↑ L. Rayleigh: On the Stability, or Instability, of certain Fluid Motions. In: Scientific Papers. Vol. 1, 1880, pp. 474-487.
2. ^ F. Noether: The turbulence problem. Journal of Applied Mathematics and Mechanics, Vol. 1, 1921, pp. 125-138.
3. ↑ L. Prandtl: Comments on the origin of turbulence. In: Journal of Applied Mathematics and Mechanics. Vol. 1, 1921, pp. 431-436.
4. ↑ W. Heisenberg: About the stability and turbulence of liquid flows. 1924.
5. ↑ W. Tollmien: About the emergence of turbulence. In: News from the Society of Sciences in Göttingen, mathematical-physical class. 1929, pp. 21-44.
6. ↑ H. Schlichting: On the emergence of turbulence in plate flow. In: News from the Society of Sciences in Göttingen, mathematical-physical class. 1933, pp. 181-208.
7. ↑ J. Pretsch: Fanning unstable disturbances in a laminar friction layer. In: Jb. German aviation research. 1942, pp. 154-171.
8. ↑ Schubauer, Skramstadt: Laminar Boundary Layer Oscillations and Transitions on a flat plate. In: NACA Report. 909, 1947.
9. ^ A. Smith, N. Gamberoni: Transition, Pressure Gradient and Stability Theory. In: Douglas Aircraft Co. Report. No. ES-26388, 1956.
10. ^ Van Ingen: A Suggested Semi-Empirical Method for the Calculation of the Boundary-Layer Transition Region. University of Delft, Report VTH-74, 1956.
11. ^ L. Mack: Boundary-layer linear stability theory. In: AGARD Special Course on Stability and Transition of Laminar Flow. AGARD R-709, 1984
12. ↑ M. Gaster: A note on the relation between temporally-increasing and spatially-increasing disturbances in hydrodynamic stability. In: Journal of Fluid Mechanics. Vol. 14, 1962, pp. 222-224.
13. ↑ HB Squire: On the Stability for Three-Dimensional Disturbances of Viscous Fluid Flow between Parallel Walls. Proc. Roy. Soc. A, Vol. 142, 1933.
14. ↑ Matrix coefficients for the compressible stability theory (website at the Institute for Aerodynamics and Gas Dynamics of the University of Stuttgart) ( Memento from June 6, 2008 in the Internet Archive )
15. ↑ W. Tollmien: A general criterion for the instability of laminar velocity distributions. In: Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikasische Klasse , Vol. I (5), 1935, pp. 79–114.
16. ^ P. Schmid, D. Henningson: Stability and Transition in Shear Flows. In: Appl. Math. Sciences. 2001, vol. 142.

See also

• Boundary layer
• Shear layer
• Direct numerical simulation

Web links

Commons : Linear Stability Theory  - Collection of Images, Videos and Audio Files