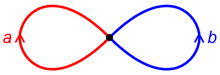
Wedge product (topology)

This article covers the wedge product of topological spaces. The roof or wedge product in a Graßmann algebra is also called a wedge product

Wedge product of two circles

With the wedge product (after wedge English wedge; also called one-point union or bouquet ) of two dotted topological spaces and one designates their disjoint union, which is glued at one point (the base point). Formally, the definition is as follows: ${\displaystyle X\vee Y}$ ${\displaystyle X}$ ${\displaystyle Y}$

${\displaystyle X\vee Y=(X\coprod Y)/(pt\coprod pt)}$

Here denotes the respective base point. ${\displaystyle pt}$

The construction can also be generalized to any set of spaces:

${\displaystyle \bigvee _{i\in I}X_{i}=(\coprod _{i\in I}X_{i})/(\coprod _{i\in I}pt_{i})}$

In a more abstract way, the wedge product can be understood as the co -product in the category of dotted topological spaces.

Role in algebraic topology

The wedge product behaves well with respect to some functors in algebraic topology . For example, for the fundamental group for locally contractible spaces ${\displaystyle X_{i}}$

${\displaystyle \pi _{1}(\bigvee _{i\in I}X_{i})=*_{i\in I}\pi _{1}(X_{i}),}$

where denotes the free product of the groups. ${\displaystyle *}$

In the singular homology :

${\displaystyle H_{n}(\bigvee _{i\in I}X_{i},pt)=\bigoplus _{i\in I}H_{n}(X_{i},pt)}$

One can wedge sum in an obvious way into the product embed the quotient ${\displaystyle X\vee Y}$ ${\displaystyle X\times Y}$

${\displaystyle X\wedge Y:=X\times Y/X\vee Y}$

is the Smash product .

In particular, the reduced suspension is of importance in the stable homotopy theory. ${\displaystyle \Sigma X:=S^{1}\wedge X}$

The wedge product is also used in the definition of the link in the homotopy groups .