Waypoint projection

The waypoint projection is a method for determining a geographic coordinate (waypoint) from a known coordinate and the specification of a distance and an angle (polar coordinate). In this case , a protractor and a ruler are applied to a point on the map whose geographic coordinates are known in order to determine the angle and distance to the point sought. The information that can be read off can then be used in a device for GPS navigation in order to display the coordinate of the point.

The angle can also be determined with a compass (after orienting the map or with a special map compass ). Any scale can be used for distance measurement (e.g. with millimeter graduation), provided the measured distance is converted for distances in nature.

The disadvantage of waypoint projection is that the curvature of the earth is not taken into account at greater distances and that there may be deviations when using distance information. Waypoint projection is often used in the field of GPS navigation, especially geocaching .

The sphere as an approximation for the shape of the earth

Derivation of the radius of the earth sphere

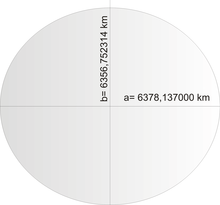
The World Geodetic System from 1984 ( WGS84 ) is often used as the reference system for position information on earth . In it, the earth has the shape of a flattened rotation ellipsoid with the two semiaxes of different lengths

${\displaystyle a=6378{,}137000\,{\mbox{km}}}$

${\displaystyle b=6356{,}752314\,{\mbox{km}}}$

The long semiaxis a extends from the center of the earth to the equator, the short semiaxis b lies on the axis of rotation of the earth and extends from the center of the earth to the north pole.

Semi-axes in the WGS84 ellipsoid

Since many calculations on ellipsoids are very complex, the shape of the earth can be approximated by a sphere for simplification. To determine the radius R of this spherical approximation, there are two approaches. In the first case one demands that the rotation ellipsoid and the globe have the same size surface, in the second case one demands that both have the same size.

The following applies to the surface F and the volume V of the WGS84 ellipsoid :

${\displaystyle \quad F=2\pi a^{2}\left(1+\left({\frac {b}{a}}\right)^{2}\cdot {\frac {\operatorname {artanh} \,\varepsilon }{\varepsilon }}\right)\quad {\mbox{mit}}\quad \varepsilon ={\sqrt {1-\left({\frac {b}{a}}\right)^{2}}}}$

${\displaystyle V={\frac {4}{3}}\pi a^{2}b}$

With the above values ​​for the two semi-axes, this results (rounded to 10 valid digits):

${\displaystyle F=510\,065\,621{,}7\,{\mbox{km}}^{2}}$

${\displaystyle V=1\,083\,207\,320\,000\,{\mbox{km}}^{3}}$

The formulas for the surface F and the volume V of a sphere can be reshaped according to the desired radius R, so that:

${\displaystyle F=4\pi R^{2}\quad \Longrightarrow \quad R={\sqrt {F/(4\pi )}}=6371{,}007181\,{\mbox{km}}}$

${\displaystyle V={\frac {4}{3}}\pi R^{3}\quad \Longrightarrow \quad R={\sqrt[{3}]{3V/(4\pi )}}=6371{,}000790\,{\mbox{km}}}$

In both cases there is a radius R of the earth sphere of

${\displaystyle \left.R=6371{,}0\,{\mbox{km}}\right.}$

Assessment of the quality of the sphere approximation

The circumference of the equator in the WGS84 ellipsoid is . With the sphere approximation it is . Therefore, the ratio can be viewed as the relative mean accuracy of the sphere approximation at the equator. Along the equator, the sphere approximation therefore underestimates the real distance by an average of 0.112%. ${\displaystyle 2\pi \cdot a}$ ${\displaystyle 2\pi \cdot R}$ ${\displaystyle (2\pi \cdot R)/(2\pi \cdot a)=0{,}99888}$

The circumference of a longitude in the WGS84 ellipsoid is equal to that of an ellipse with the semi-axes a and b. The circumference of an ellipse can be approximated using the following formula:

${\displaystyle U_{WGS84}\approx \pi (a+b)\left(1+{\frac {3\lambda ^{2}}{10+{\sqrt {4-3\lambda ^{2}}}}}\right)\quad ;\quad \lambda ={\frac {a-b}{a+b}}}$

The relative mean accuracy of the sphere approximation along a degree of longitude is therefore . A distance along a longitude circle is overestimated by about 0.056% in the sphere approximation. ${\displaystyle (2\pi \cdot R)/U_{WGS84}=1{,}00056}$

Therefore, the relative deviation of the sphere approximation from the underlying rotational ellipsoid is in the per mil range and is negligible for most applications.

Great circles and small circles

For all circles on the surface of the sphere, the center of the circle lies within the sphere. In a so-called great circle , the center of the circle is exactly at the same point as the center of the sphere. Therefore, a great circle always has the maximum possible radius, which explains the name. All circles that are not great circles are called small circles . Its center never lies in the center of the sphere and its radius is always smaller than the radius of the earth. The equator and all longitudes are great circles. All latitudes, except for the equator, are small circles.

Since all small circles have a smaller radius than the great circles, small circles are also more curved. If you move along a small circle from a point A to a point B, the path is longer than if you move from A to B on a great circle. Therefore the shortest connection ( orthodrome ) between two points A and B is always on a great circle. Against this background, great circles on a spherical surface have the same meaning as straight lines in a plane.

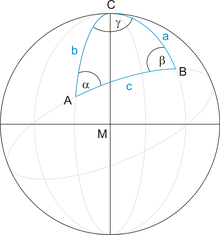
Sphere triangles

Spherical triangle with the north pole as a corner point

A triangle is delimited by three straight lines in one plane. Correspondingly, a spherical triangle is delimited by three great circles on a spherical surface. The points of intersection of the great circles are the corner points of the spherical triangle. To simplify navigation calculations with spherical triangles, all lengths and distances are given relative to the earth's radius R:

${\displaystyle a={\frac {\overline {BC}}{R}}\quad ;\quad b={\frac {\overline {AC}}{R}}\quad ;\quad c={\frac {\overline {AB}}{R}}}$

That means, before starting all calculations, all lengths are divided by the earth's radius. For navigation calculations, the earth is, so to speak, shrunk to the unit sphere with a radius of 1 m. Because the maximum possible distance on the earth's surface is equal to the circumference of a great circle, this transformation transforms all length information into the value range from to and can thus be understood as angles (in radians). If, according to the calculation, the result is a length or distance, this must be converted back to the earth sphere by multiplying it by the earth's radius. ${\displaystyle 2\pi R}$ ${\displaystyle 0}$ ${\displaystyle 2\pi }$

From the article spherical trigonometry , the most important formulas for calculating with spherical triangles (on the unit sphere) are listed below, which are required in the further derivation.

Sine law

${\displaystyle {\frac {\sin a}{\sin \alpha }}={\frac {\sin b}{\sin \beta }}={\frac {\sin c}{\sin \gamma }}}$

Side cosine law

${\displaystyle \,\cos a=\cos b\cdot \cos c+\sin b\cdot \sin c\cdot \cos \alpha }$

${\displaystyle \,\cos b=\cos a\cdot \cos c+\sin a\cdot \sin c\cdot \cos \beta }$

${\displaystyle \,\cos c=\cos a\cdot \cos b+\sin a\cdot \sin b\cdot \cos \gamma }$

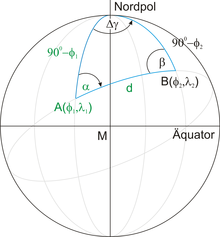
Derivation of the waypoint projection on the globe

A point is given by its latitude and longitude , a bearing angle and a distance to an unknown point . The latitude and longitude of the destination must be determined. All known sizes are shown in green in the illustration. ${\displaystyle A(\phi _{1},\lambda _{1})}$ ${\displaystyle \phi _{1}}$ ${\displaystyle \lambda _{1}}$ ${\displaystyle \alpha }$ ${\displaystyle {\overline {AB}}}$ ${\displaystyle B(\phi _{2},\lambda _{2})}$ ${\displaystyle \phi _{2}}$ ${\displaystyle \lambda _{2}}$

Spherical triangle with the north pole as a corner point

The distance d is the distance between the two points A and B transformed to the unit sphere:

${\displaystyle d={\frac {\overline {AB}}{R}}\quad {\mbox{(in Rad)}}}$

Because latitude and longitude are usually given in degrees, in the following derivation all angles should be measured in degrees, for this d must be converted into degrees:

${\displaystyle d={\frac {\overline {AB}}{R}}\,{\frac {180^{\circ }}{\pi }}={\frac {\overline {AB}}{111{,}2\,{\mbox{km}}}}\quad {\mbox{(in Grad)}}}$

Since latitude is measured from the equator, the distance of point A from the north pole is the same . Similarly, the distance of the searched point B from the north pole is the same . ${\displaystyle (90^{\circ }-\phi _{1})}$ ${\displaystyle (90^{\circ }-\phi _{2})}$

Exact formulas

According to the side cosine law:

${\displaystyle \cos \left(90^{\circ }-\phi _{2}\right)=\cos \left(90^{\circ }-\phi _{1}\right)\cos d+\sin \left(90^{\circ }-\phi _{1}\right)\sin d\cos \alpha }$

Because of and it follows from this: ${\displaystyle \cos(90^{\circ }-x)=\sin(x)}$ ${\displaystyle \sin(90^{\circ }-x)=\cos(x)}$

${\displaystyle \left.\sin \phi _{2}=\sin \phi _{1}\cos d+\cos \phi _{1}\sin d\cos \alpha \right.}$

To determine the longitude of the target point B, the sine law provides the change in latitude: ${\displaystyle \lambda _{2}}$ ${\displaystyle \Delta \lambda =\lambda _{2}-\lambda _{1}}$

${\displaystyle {\frac {\sin \Delta \lambda }{\sin d}}={\frac {\sin \alpha }{\sin \left(90^{\circ }-\phi _{2}\right)}}={\frac {\sin \alpha }{\cos \phi _{2}}}}$

With the inverse function it finally follows for the searched coordinates of the target point: ${\displaystyle \arcsin }$

${\displaystyle \phi _{2}=\arcsin \left(\sin \phi _{1}\cos d+\cos \phi _{1}\sin d\cos \alpha \right)\quad ;\quad \lambda _{2}=\lambda _{1}+\arcsin \left({\frac {\sin d}{\cos \phi _{2}}}\,\sin \alpha \right)}$

Attention: With these formulas it should be noted that the arcsin function is normalized to the range from to . The calculated values ​​therefore have to be adjusted to the actual position of the points in a case distinction. ${\displaystyle -90^{\circ }}$ ${\displaystyle +90^{\circ }}$

Approximation formulas for small distances

For short (much less than 111 km) distances between points A and B, the parameter d from the formulas derived above becomes less than 1 degree. Accordingly, the difference between the target latitude and the starting latitude becomes very small. Hence the (exact) relationship derived above ${\displaystyle \Delta \phi :=\phi _{2}-\phi _{1}}$ ${\displaystyle \phi _{2}}$ ${\displaystyle \phi _{1}}$

${\displaystyle \left.\sin \phi _{2}=\sin \phi _{1}\cos d+\cos \phi _{1}\sin d\cos \alpha \right.}$

with the following Taylor series expansion (up to the 2nd order)

${\displaystyle \sin \phi _{2}=\sin \left(\phi _{1}+\Delta \phi \right)\approx \sin \phi _{1}+\cos \phi _{1}\cdot \Delta \phi -{\frac {1}{2}}\sin \phi _{1}\cdot (\Delta \phi )^{2}}$

${\displaystyle \cos d\approx \underbrace {\cos 0} _{=1}-\underbrace {\sin 0} _{=0}\cdot d-{\frac {1}{2}}\underbrace {\cos 0} _{=1}\cdot d^{2}=1-{\frac {d^{2}}{2}}}$

${\displaystyle \sin d\approx \underbrace {\sin 0} _{=0}+\underbrace {\cos 0} _{=1}\cdot d-{\frac {1}{2}}\underbrace {\sin 0} _{=0}\cdot d^{2}=d}$

simplify as follows:

${\displaystyle \sin \phi _{1}+\cos \phi _{1}\cdot \Delta \phi -{\frac {1}{2}}\sin \phi _{1}\cdot (\Delta \phi )^{2}\approx \sin \phi _{1}\cdot \left(1-{\frac {d^{2}}{2}}\right)+\cos \phi _{1}\cdot d\cdot \cos \alpha }$

On both sides of the approximation, the following is first subtracted: ${\displaystyle \sin \,\phi _{1}}$

${\displaystyle \cos \phi _{1}\cdot \Delta \phi -{\frac {1}{2}}\sin \phi _{1}\cdot (\Delta \phi )^{2}\approx -\sin \phi _{1}\cdot {\frac {d^{2}}{2}}+\cos \phi _{1}\cdot d\cdot \cos \alpha }$

and then both sides are divided by: ${\displaystyle \cos \,\phi _{1}}$

${\displaystyle \Delta \phi -{\frac {1}{2}}\tan \phi _{1}\cdot (\Delta \phi )^{2}\approx -\tan \phi _{1}\cdot {\frac {d^{2}}{2}}+d\cdot \cos \alpha }$

Finally, the tangent function can still be collected on the right side:

${\displaystyle \Delta \phi \approx d\cdot \cos \alpha +\tan \phi _{1}\cdot {\frac {\left(\Delta \phi \right)^{2}-d^{2}}{2}}}$

Because of this , the tangent term can essentially be neglected: ${\displaystyle d\ll 1^{\circ }}$

${\displaystyle \Delta \phi \approx d\cdot \cos \alpha }$

However, the tangent term has two major consequences for the accuracy of the approximation for : ${\displaystyle \Delta \,\phi }$

• At small angles , i.e. near the equator, is very small. Therefore the tangent term is also very small and the result is very precise. However, with increasing latitude the tangent function grows faster and faster until it becomes infinitely large. Therefore, the accuracy of the approximation decreases with increasing distance from the equator. ${\displaystyle \phi _{1}}$ ${\displaystyle \tan \,\phi _{1}}$ ${\displaystyle \phi _{1}}$ ${\displaystyle 90^{\circ }}$ ${\displaystyle \Delta \phi }$

• Even with a large tangent value, the result of the approximation is still very precise if and d are approximately the same size. This is all the more the case, the more parallel the route from A to B to a degree of longitude, i.e. the more the bearing angle points in the direction of a pole (0 or 180 degrees). ${\displaystyle \Delta \phi }$ ${\displaystyle \alpha }$

In other words, the more inaccuracy you are, the further away you are from the equator and the more the bearing is parallel to the equator (towards east or west)!

The approximation for calculating the change in longitude is still missing . Based on the exact relationship already derived above, the sine functions are again approximated with very small arguments: ${\displaystyle \Delta \lambda }$ ${\displaystyle \Delta \lambda }$

${\displaystyle {\frac {\sin \Delta \lambda }{\sin d}}={\frac {\sin \alpha }{\cos \phi _{2}}}\rightarrow {\frac {\Delta \lambda }{d}}\approx {\frac {\sin \alpha }{\cos \left(\phi _{1}+\Delta \phi \right)}}}$

Multiplying both sides by d finally gives:

${\displaystyle \Delta \lambda \approx {\frac {d}{\cos \left(\phi _{1}+\Delta \phi \right)}}\,\cdot \sin \alpha }$

Since these approximation formulas only apply to short distances d, the coordinates of the starting point will only change by small values . It is therefore advisable to formulate the approximation formulas in such a way that they deliver the result directly in arc minutes. To do this, d is converted into minutes of arc ${\displaystyle A(\phi _{1},\lambda _{1})}$ ${\displaystyle (\Delta \phi ,\Delta \lambda )}$

${\displaystyle d={\frac {\overline {AB}}{R}}\,{\frac {180\cdot 60'}{\pi }}={\frac {\overline {AB}}{1853\,{\mbox{m}}}}\quad {\mbox{(in Bogenminuten)}}}$

and inserted into the two approximation formulas:

${\displaystyle \Delta \phi \approx {\frac {\overline {AB}}{1853\,{\mbox{m}}}}\cdot \cos \alpha \quad ;\quad \Delta \lambda \approx {\frac {\overline {AB}}{1853\,{\mbox{m}}}}\cdot {\frac {\sin \alpha }{\cos \left(\phi _{1}+\Delta \phi \right)}}\quad {\mbox{(in Bogenminuten)}}}$

Since the value of must obviously already be known in order to calculate from , the estimate for the change in longitude can be written even shorter: ${\displaystyle \Delta \lambda }$ ${\displaystyle \Delta \phi }$

${\displaystyle \Delta \lambda \approx \Delta \phi \cdot {\frac {\tan \alpha }{\cos \left(\phi _{1}+\Delta \phi \right)}}}$

Remarks:

• The cosine function in the denominator of the approximation of takes into account the fact that the circumference of the circle of latitude is shortened by the cosine of the corresponding degree of latitude (circles of latitude are not great circles). ${\displaystyle \Delta \lambda }$ ${\displaystyle (\phi _{1}+\Delta \phi )}$

• The derived formulas also apply if point A or point B or both points A, B are in the southern hemisphere. The distance of such a point from the North Pole is greater than on the unit sphere . Since the latitudes from the equator to the south pole are measured with negative degrees, z. B. the term at negative to an angle greater than measured from the North Pole. ${\displaystyle 90^{\circ }}$ ${\displaystyle (90^{\circ }-\phi _{1})}$ ${\displaystyle \phi _{1}}$ ${\displaystyle 90^{\circ }}$

• The approximation found is roughly the same as that which results from a planar waypoint projection. The only but important difference is that when calculating the cosine, the latitude of the target point is used, and not (as with the plane) the latitude of the starting point. In the derived case, the estimate for is more accurate than one meter, even with large distances (up to 70 kilometers!) Between A and B! ${\displaystyle \Delta \lambda }$ ${\displaystyle \Delta \lambda }$

Goodness of the approximation formulas

As described above, the estimate for the change in longitude up to a distance of 70 km is more accurate than one meter. Hence, virtually all of the inaccuracy lies in the calculation of the change in latitude . The following table shows the maximum distance from A to B in meters, depending on the latitude, so that the result of the simple approximation deviates from the exact solution for less than 1 meter or less than 5 meters. The worst values ​​are given in each case, i.e. the case that one moves parallel to the equator. ${\displaystyle \Delta \lambda }$ ${\displaystyle \Delta \phi }$ ${\displaystyle \Delta \phi }$

Latitude	0	10	20th	30th	40	50	60	70	80	85	89
<1 meter	87,251	8,499	5,916	4,697	3,896	3,269	2.712	2.153	1,498	1,055	471
<5 meters	148,455	19.009	13,231	10,505	8,714	7,312	6,065	4,815	3,351	2,361	1,054

Here are some reading examples:

• At the 50th parallel, the approximation formula is more accurate than 1 meter up to a distance of 3269 meters.
• At the 60th parallel, the approximation formula is more accurate than 5 meters up to a distance of 6065 meters.

The northernmost point of Germany is known to be the island of Sylt with a latitude of 54.55 °. Therefore, the approximation formulas can be used in Germany up to a distance of about 3 km without hesitation in order to be able to make very precise position determinations.

See also

• Main geodetic task
• Cross bearing

literature

• Uli Benker: GPS navigation. (For hikers, mountaineers, bikers; basics of navigation, tour planning with map and PC, tips on purchasing equipment) . 2nd revised edition. Bruckmann Verlag, Munich 2008, ISBN 978-3-7654-5160-7 .
• Thomas Froitzheim: GPS. The manual for mountain bikes, racing bikes and touring bikes . Bruckmann Verlag, Munich 2009, ISBN 978-3-7654-50167 .

Web links

• cs.cmu.edu Waypoint Projection, accessed April 3, 2009
• zwanziger.de Internet site for the use of waypoint projection